Ein schneller »Drawline«-Algorithmus
Im folgenden wird eine Möglichkeit vorgestellt, schnell und einfach eine Strecke, die durch ihre beiden Endpunkte gegeben ist, zu plotten. Als Ausgabegerät können Bildschirm, Drucker oder Plotter eingesetzt werden.
Der Algorithmus wird in einer Basic- und einer Assembler-Version für einen 6502-Mikroprozessor mit den Adressen für den Commodore 64 (der 6510 Mikroprozessor im C 64 ist im Befehlssatz identisch mit dem 6502) beschrieben. Die Programme können, da sie im Aufbau einfach sind und erklärt werden, ohne große Probleme für andere Systeme beziehungsweise andere Sprachen umgewandelt werden.
Vor einiger Zeit suchte ich eine Möglichkeit, das in [1] auf Seite 97 abgedruckte, in Assembler geschriebene Programm um eine einfache aber doch effiziente »Drawline«-Routine zu erweitern. In [2] fand ich genau den Algorithmus, den ich brauchte, — nur war er »leider« in Basic formuliert. Jedoch bereitete es, nachdem der Algorithmus verstanden war, nicht mehr allzu viel Mühe, eine Assemblerversion zu schreiben. Doch vor der Beschreibung der Programme eine kurze Erklärung des Algorithmus.
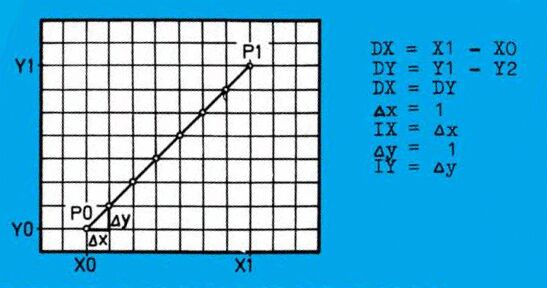
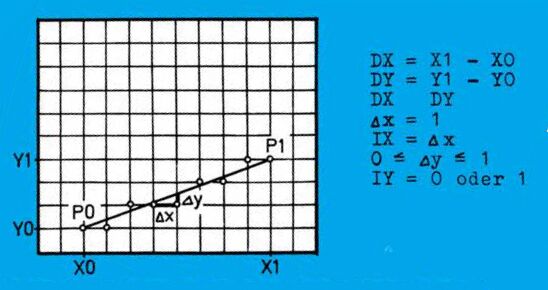
Ein Rasterbildschirm setzt sich aus einzelnen Punkten, die gesetzt oder auch gelöscht sein können, zusammen. Der Abstand der Punkte voneinander ist in der Richtung der Achsen immer gleich und jeweils eine Schrittweite groß (Bild 1). Um eine Gerade zwischen den Punkten P0 und P1 zu ziehen, muß daher schrittweise berechnet werden, welcher Punkt der Ideallinie (Bild 2) am nächsten ist und daher gesetzt werden muß.
Geschwindigkeitsvorteile durch einfache Berechnungen
Für diese Berechnungen gibt es verschiedene Möglichkeiten, doch sind sie meistens mit Multiplikationen und Divisionen in der Approximationsschleife verbunden und daher weder schnell noch einfach zu programmieren. Der hier vorgestellte Algorithmus verwendet dagegen nur eine Division und in der Schleife nur mehr Addition, Subtraktion und eine Vergleichsoperation. Da die Schleifenoperationen außerdem nur mehr an Integerzahlen durchzuführen sind, ist er besonders schnell, und er läßt sich auch einfach programmieren. Zur Erklärung soll eine Gerade mit einer Steigung zwischen 0 und 1 (0 bis 45 Grad) betrachtet werden.
Wie man in Bild 2 unschwer erkennen kann, ist der Abstand der Punkte P0 und P1 entlang der X-Achse gleich der Anzahl der zu setzenden Punkte, DX = X1 — X0, das heißt es sind DX-Approximationen durchzuführen, um die Gerade zu zeichnen. Für jeden folgenden Punkt ist also X0 um IX (= 1) zu erhöhen, während Y0 gleichbleibt (IY = 0) oder ebenfalls um 1 (IY = 1) erhöht wird. Der Abstand der beiden Punkte entlang der Y-Achse ist demnach: DY = Y1 — Y0. Es bleibt also nur mehr festzustellen, wann IY = 0, beziehungsweise IY = 1 zu sein hat. Dazu wird vor Beginn der Schleife ein Approximationswert OF berechnet. Da beim Idealfall für eine Steigung von 1 (Bild 1) IY = IX, das heißt immer 1 ist, und DX = DY ist, wird OF = DX/2.
Rasterpunkte optimieren
Zu OF wird für jeden neuen Punkt DY addiert. Solange OF kleiner als DX bleibt, bleibt IY = 0, wird OF gleich oder größer, so wird IY = 1, das heißt Y0 um 1 erhöht. Damit diese Abfrage auch für die folgenden Punkte möglich ist, muß OF um DX vermindert werden. Wenn DX-Punkte gesetzt worden sind, sind alle Punkte der Geraden berechnet und die Schleife kann verlassen werden.
Soweit also für eine Gerade mit positiver Steigung zwischen 0 und 45 Grad Wie sieht es aber aus, wenn zum Beispiel X1 kleiner X0 ist? Nun, dann wird eben IX = —1, X0 also für jeden Aproximationsschritt um 1 erniedrigt. Und wie sieht es für eine Steigung größer 1 aus? Auch dieses Problem läßt sich einfach lösen. Es werden für die Rechnung einfach die beiden Achsen vertauscht.
Der Ablauf beider Programme ist im Nassi-Shneiderman-Diagramm (Bild 3) dargestellt. Zum leichteren Vergleich sind alle Variablenbezeichnungen in den Programmen identisch.
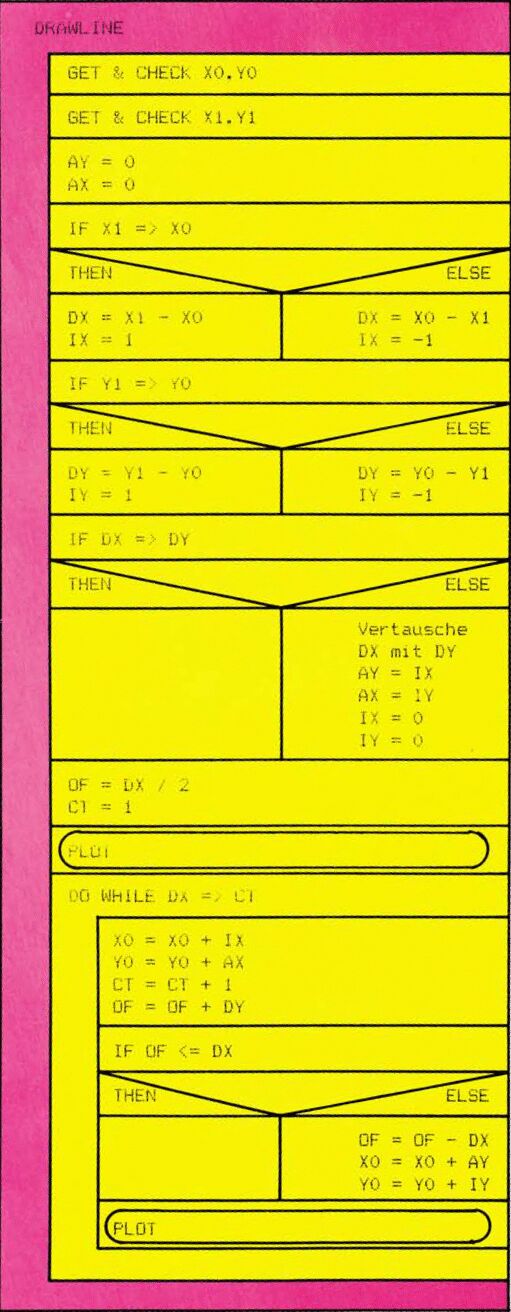
Die Basic-Version gibt nur die Koordinaten der berechneten Punkte aus, da ich dafür keine »Setze-Punkt«-Routine schreiben wollte. Man kann aber die Wirkungsweise des Algorithmus schön verfolgen.
Das Assemblerprogramm ist, wie schon oben gesagt, für den C 64 geschrieben mit einer möglichen Auflösung von 320 x 200 Punkten. Dadurch können die Werte für Y in einem Byte untergebracht werden, während für X zwei Byte benötigt werden. OF, DX und der Schleifenzähler CT benötigen deshalb ebenfalls 2 Byte. Die Länge der Werte muß beim Umstricken für ein anderes System berücksichtigt werden, da alle durchzuführenden Operationen dementsprechend 1 oder 2 Byte lang sind.
In dieser Assemblerversion werden nur 2 Subroutinen aus dem Betriebssystem verwendet. Sie sind in Tabelle 1 beschrieben. Zusätzlich habe ich die Adressen für die anderen Commodore Computer angegeben Die Subroutine »PLOT« muß, wenn sie sich im Betriebssystem wie bei den Commodoresystemen nicht findet, extra geschrieben werden. Für den C 64 findet man in [1] ein geeignetes Programm.
Kein Problem: Variablen
In Tabelle 2 sind alle verwendeten Variablen aufgelistet und beschrieben. Aufgerufen wird diese Version mit SYS aaaa,X0,Y0,X1,Y1 wobei aaaa die Startadresse der Routine, X0/Y0 und X1/Y1 die Koordinaten der beiden Punkte sind. Für die Koordinaten können auch Ausdrücke verwendet werden, da die Betriebssystemroutine »GETCOR« auch Ausdrücke auswertet.
Zusätzliche Erweiterungen
Den Lesern, die mit Assembler-Programmen noch etwas Probleme haben, sende ich gerne gegen einen Kostenbeitrag von 10 Mark eine Kassette mit einem Basic-Lader mit dem gesamten Programm zu. Es stehen dann neben den in [1] beschriebenen Befehlen noch DRAWLINE, ERASELINE, DRAWX-AXIS, ERASEX-AXIS, DRAWY-AXIS und ERASEY-AXIS zur Verfügung.
Bei der Anwendung dieses Algorithmus wünsche ich viel Spaß und Erfolg.
(Michael Bauer)Literatur:
(1) Angerhausen et al.; »64 Intern« Seiten 97-100. DATA BECKER 1983
(2) Higgins, Mike; »Fast Line-Drawing Technique« Seiten 414-416; BYTE August 1981
100 rem drawline 110 rem diese routine berechnet die koordinaten 120 rem der punkte einer strecke, die durch ihre 130 rem endpunkte gegeben ist. mit einer ge- 140 rem eigneten 'setpoint'-routine kann der 150 rem bildschirm oder ein plotter angesteuert 160 rem werden. die grenzen der werte fuer x und 170 rem y entsprechen den werten fuer den hi-res 180 rem bildschirm des commodore 64. 190 rem 200 rem das original dieses programmes von mike 210 rem higgins ist in byte heft 8/81 auf den 220 rem seiten 414 - 416 erschienen. 230 rem 240 rem michael bauer aindorferstr. 86 8 muenchen 21 250 rem 260 rem get & check x0/y0 270 input"koordinaten 1. punkt";x0,y0 280 ifx0>319ory0>199then270 290 ifx0<0ory0<0then270 300 rem get & check x1/y1 310 input"koordinaten 2. punkt";x1,y1 320 ifx1>319ory1>199then310 330 ifx1<0ory1<0then310 340 rem initialisiere variable 350 ay=0:iy=1:ix=1:ax=0 360 rem pruefe steigung 370 ifx1=>x0thendx=x1-x0:goto400 380 ix=-1 390 dx=x0-x1 400 ify1=>y0thendy=y1-y0:goto440 410 dy=y0-y1 420 iy=-1 430 rem steigung > 1? 440 ifdx=>dythen530 450 ct=dx:rem vertausche dx und dy 460 dx=dy 470 dy=ct 480 ay=ix 490 ix=0 500 ax=iy 510 iy=0 520 rem berechne approximationswert 530 of=dx/2 540 ct=1:rem schleifenzaehler 550 goto660:rem plotte ursprungspunkt 560 rem ******** approximationsschleife 570 x0=x0+ix 580 y0=y0+ax 590 of=of+dy 600 ct=ct+1 610 rem y0 erhoehen ? 620 ifof<=dxthen660 630 of=of-dx 640 x0=x0+ay 650 y0=y0+iy 660 printx0,y0 670 rem letzter punkt ? 680 ifdx=>ctthen570 690 end
0000 1 ;algorithmus basiert auf einen artikel von mike 0000 2 ;higgins erschienen in der byte august 1981 s.414-416 0000 3 ; 0000 4 ;das programm fuer den cbm 64 wurde von 0000 5 ;michael bauer aindorferstr. 86 8000 muenchen 21 0000 6 ;geschrieben. 0000 7 ; 0014 8 x0 = $14 ;x-koordinate 00fd 9 y1 = $fd ;y-koordinate aefd 10 chkcom = $aefd ;prueft ob ein komma folgt, 0000 11 ; wenn ja, holt das naechste 0000 12 ; zeichen, wenn nein -> syntax 0000 13 ; error b7eb 14 getcor = $b7eb ;holt eine adresse (= 2 byte) 0000 15 ; und ein byte. die adresse wird 0000 16 ; in x0 und x0+1, das byte im 0000 17 ; x-register uebergeben 0000 18 plot = $0000 ;die adresse dieser routine 0000 19 ; muss hier eingesetzt werden. 0000 20 ; plot muss in der lage sein 0000 21 ; einen punkt, dessen x und y 0000 22 ; koordinate uebergeben werden, 0000 23 ; zu setzen. 0000 24 ; c178 25 * = $c178 c178 26 ; c178 60 27 ill rts c179 28 ;********* einsprung: aufrus sys49529,x0,y0,x1,y1 c179 20efc2 29 drwlin jsr gcoord ;hole koordinaten 1. punkt c17c b0fa 30 bcs ill ;ignoriere wert wenn ausserhalb c17e 8e09c3 31 stx y0 c181 8d10c3 32 sta ct+1 c184 8c0fc3 33 sty ct c187 20efc2 34 jsr gcoord ;hole koordinaten 2. punkt c18a b0ec 35 bcs ill ;ignoriere wert wenn ausserhalb c18c 86fd 36 stx y1 c18e 8c0ac3 37 sty x1 c191 ac0fc3 38 ldy ct c194 8414 39 sty x0 c196 8d0bc3 40 sta x1+1 c199 ad10c3 41 lda ct+1 c19c 8515 42 sta x0+1 c19e a001 43 setpar ldy #$01 ;(yr) = 1 c1a0 8c14c3 44 sty ix c1a3 8c11c3 45 sty iy c1a6 8c0fc3 46 sty ct c1a9 88 47 dey ;(yr) = 0 c1aa 8c10c3 48 sty ct+1 c1ad 8c13c3 49 sty ax c1b0 8c12c3 50 sty ay c1b3 88 51 dey ;(yr) = - 1 c1b4 52 ; berechne dx c1b4 ad0bc3 53 begin lda x1+1 ;x1 => x0 ? c1b7 c515 54 cmp x0+1 c1b9 9009 55 bcc draw01 ;nein -> c1bb d01e 56 bne draw02 ;ja -> c1bd ad0ac3 57 lda x1 c1c0 c514 58 cmp x0 c1c2 b017 59 bcs draw02 ;ja -> c1c4 38 60 draw01 sec ;dx = x0 - x1 c1c5 a514 61 lda x0 c1c7 ed0ac3 62 sbc x1 c1ca 8d0dc3 63 sta dx c1cd a515 64 lda x0+1 c1cf ed0bc3 65 sbc x1+1 c1d2 8d0ec3 66 sta dx+1 c1d5 8c14c3 67 sty ix ;ix = -1 c1d8 4cecc1 68 jmp draw03 c1db 38 69 draw02 sec ;dx = x1 - x0 c1dc ad0ac3 70 lda x1 c1df e514 71 sbc x0 c1e1 8d0dc3 72 sta dx c1e4 ad0bc3 73 lda x1+1 c1e7 e515 74 sbc x0+1 c1e9 8d0ec3 75 sta dx+1 c1ec 76 ; berechne dy c1ec a5fd 77 draw03 lda y1 ;y1 => y0 ? c1ee cd09c3 78 cmp y0 c1f1 b00f 79 bcs draw04 ;ja -> c1f3 38 80 sec ;dy = y0 - y1 c1f4 ad09c3 81 lda y0 c1f7 e5fd 82 sbc y1 c1f9 8d0cc3 83 sta dy c1fc 8c11c3 84 sty iy ;iy = -1 c1ff 4c08c2 85 jmp draw05 c202 ed09c3 86 draw04 sbc y0 ;dy = y1 - y0 c205 8d0cc3 87 sta dy c208 ad0ec3 88 draw05 lda dx+1 ;dx < dy ? c20b d024 89 bne draw07 ;nein -> c20d ad0dc3 90 lda dx c210 cd0cc3 91 cmp dy c213 b01c 92 bcs draw07 ;nein -> c215 ae0cc3 93 ldx dy ;vertausche die achsen c218 8d0cc3 94 sta dy c21b 8e0dc3 95 stx dx c21e ad14c3 96 lda ix ;ay = ix c221 8d12c3 97 sta ay c224 ad11c3 98 lda iy ;ax = iy c227 8d13c3 99 sta ax c22a c8 100 iny ;(yr) = 0 c22b 8c14c3 101 sty ix ;ix = 0 c22e 8c11c3 102 sty iy ;iy = 0 c231 ad0ec3 103 draw07 lda dx+1 ;of = dx / 2 c234 4a 104 lsr a c235 8d0bc3 105 sta of+1 ;= 0 c238 ad0dc3 106 lda dx c23b 6a 107 ror a c23c 8d0ac3 108 sta of c23f 4cd5c2 109 jmp plotit ;plotte 1. punkt c242 110 ;********* approximationsschleife c242 ad14c3 111 drwlop lda ix ;ix = 01 c245 300e 112 bmi draw08 ;ja -> weiter c247 18 113 clc ;x0 = x0 + ix c248 6514 114 adc x0 c24a 8514 115 sta x0 c24c a515 116 lda x0+1 c24e 6900 117 adc #$00 c250 8515 118 sta x0+1 c252 4c62c2 119 jmp draw11 c255 38 120 draw08 sec ;x0 = x0 - ix c256 a514 121 lda x0 c258 e901 122 sbc #$01 c25a 8514 123 sta x0 c25c a515 124 lda x0+1 c25e e900 125 sbc #$00 c260 8515 126 sta x0+1 c262 18 127 draw11 clc ;y0 = y0 + ax c263 ad09c3 128 lda y0 c266 6d13c3 129 adc ax c269 8d09c3 130 sta y0 c26c 18 131 clc ;of = of + dy c26d ad0ac3 132 lda of c270 6d0cc3 133 adc dy c273 8d0ac3 134 sta of c276 ad0bc3 135 lda of+1 c279 6900 136 adc #$00 c27b 8d0bc3 137 sta of+1 c27e ee0fc3 138 inc ct ;ct = ct + 1 c281 d003 139 bne draw06 c283 ee10c3 140 inc ct+1 c286 ad0bc3 141 draw06 lda of+1 ;of <= dx ? c289 cd0ec3 142 cmp dx+1 c28c 9047 143 bcc plotit ;ja -> zeichne punkt c28e d008 144 bne draw09 c290 ad0dc3 145 lda dx c293 cd0ac3 146 cmp of c296 b03d 147 bcs plotit ;ja -> zeichne punkt c298 38 148 draw09 sec ;of = of - dx c299 ad0ac3 149 lda of c29c ed0dc3 150 sbc dx c29f 8d0ac3 151 sta of c2a2 ad0bc3 152 lda of+1 c2a5 ed0ec3 153 sbc dx+1 c2a8 8d0bc3 154 sta of+1 c2ab ad12c3 155 lda ay ;ay = -1 ? c2ae 300e 156 bmi draw10 ;ja -> weiter c2b0 18 157 clc ;x0 = x0 + ay c2b1 6514 158 adc x0 c2b3 8514 159 sta x0 c2b5 a515 160 lda x0+1 c2b7 6900 161 adc #$00 c2b9 8515 162 sta x0+1 c2bb 4ccbc2 163 jmp draw12 c2be 38 164 draw10 sec ;x0 = x0 - ay c2bf a514 165 lda x0 c2c1 e901 166 sbc #$01 c2c3 8514 167 sta x0 c2c5 a515 168 lda x0+1 c2c7 e900 169 sbc #$00 c2c9 8515 170 sta x0+1 c2cb 18 171 draw12 clc ;y0 = y0 + iy c2cc ad09c3 172 lda y0 c2cf 6d11c3 173 adc iy c2d2 8d09c3 174 sta y0 c2d5 ae09c3 175 plotit ldx y0 ;uebergebe y0 im (cr) an plot c2d8 200000 176 jsr plot ;zeichne punkt c2db ad10c3 177 lda ct+1 ;ct <= dx ? c2de cd0ec3 178 cmp dx+1 c2e1 9009 179 bcc nexpnt ;nein -> naechster punkt c2e3 ad0dc3 180 lda dx c2e6 cd0fc3 181 cmp ct c2e9 b001 182 bcs nexpnt c2eb 60 183 rts ;linie ist fertig gezeichnet c2ec 4c42c2 184 nexpnt jmp drwlop c2ef 185 ; c2ef 20fdae 186 gcoord jsr chkcom ;hole und pruefe parameter c2f2 20ebb7 187 jsr getcor c2f5 e0c8 188 cpx #200 ;y > 200 ? c2f7 b00c 189 bcs finish c2f9 a515 190 lda x0+1 ;x > 320 ? c2fb c901 191 cmp #$01 c2fd 9007 192 bcc finis ;< 1 c2ff d004 193 bne finish ;> 1 c301 a414 194 ldy x0 ;= 1 c303 c040 195 cpy #$40 c305 60 196 finish rts c306 a414 197 finis ldy x0 c308 60 198 rts c309 199 ; c309 200 ; arbeisvariable c309 201 ; c309 202 y0 = * ;y-koordinate c30a 203 x1 = y0+1 ;x-koordinate c30a 204 of = x1 ;approximationswert c30c 205 dy = of+2 ;abstand y1 zu y0 c30d 206 dx = dy+1 ;anzahl der punkte c30f 207 ct = dx+2 ;schleifenzaehler c311 208 iy = ct+2 ;inkrement c312 209 ay = iy+1 ;wie iy c313 210 ax = ay+1 ;wie ix c314 211 ix = ax+1 ;inkrement c309 212 .end x0 = 0014 y1 = 00fd chkcom = aefd getcor = b7eb plot = 0000 ill = c178 drwlin = c179 setpar = c19e begin = c1b4 draw01 = c1c4 draw02 = c1db draw03 = c1ec draw04 = c202 draw05 = c208 draw07 = c231 drwlop = c242 draw08 = c255 draw11 = c262 draw06 = c286 draw09 = c298 draw10 = c2be draw12 = c2cb plotit = c2d5 nexpnt = c2ec gcoord = c2ef finish = c305 finis = c306 y0 = c309 x1 = c30a of = c30a dy = c30c dx = c30d ct = c30f iy = c311 ay = c312 ax = c313 ix = c314 690 END
| Name | Adressen | Beschreibung | |||||
|---|---|---|---|---|---|---|---|
| 2001 | 3032 | 9032 | VC20 | C 64 | 610/710 | ||
| CHKCOM | $CE11 | $CDF8 | $BEF5 | $CEFD | $AEFD | $9730 | Prüfe, ob nächstes Zeichen im BASIC-Text ein Komma ist, wenn nicht gebe 'SYNTAX ERROR' aus |
| GETCOR | $D6C4 | $D6C6 | $C921 | $D7EB | $B7EB | $B4E5 | Holt die Koordinaten eines Punktes aus dem BASIC-Text. Die Routine wertet auch Ausdrücke aus. Die X-Koordinate wird als 2-Byte-Wert in X0, die Y-Koordinate als Byte im X-Register übergeben. |
| X0 | $0066 | $0014 | $0014 | $0014 | $0014 | $0011 | Hier wird die X-Koordinate von GERCOR abgelegt. |
| PLOT | -- | -- | -- | -- | -- | -- | Diese Routine ist keine Betriebssystemroutine. Sie übernimmt die Koordinaten von X0 und dem X-Register. |
| Name | Beschreibung |
|---|---|
| X0,Y0 | Koordinaten des ersten Punktes |
| X1,X1 | Koordinaten des zweiten Punktes |
| CT | Schleifenzähler |
| IX | Inkrement oder Dekrement für X0 (-1,0,+1) |
| IY | Inkrement oder Dekrement für Y0 (-1,0,+1) |
| AX | Wie IX für Steigungen > 1 |
| AY | Wie IY für Steigungen > 1 |
| DX | Entfernung der Punkte entlang der X-Achse (= Anzahl der Punkte) |
| DY | Entfernung der Punkte entlang der Y-Achse |
| OF | Approximationsvariable zur Bestimmung ob Y0 gleichbleibt |
