Reise durch die Wunderwelt der Grafik – Teil 5
Nachdem wir sie in den ersten vier Folgen kaum erwähnt haben, sind sie heute dran: die Sprites. Sie müssen einfach in jeder Reise durch die Grafik unseres C 64 auftauchen.
Sprite heißt auf deutsch soviel wie »Kobold«, »Gespenst«. Wie richtige Kobolde können sie sowohl in Dornröschens Schloß (also im Bit-Map-Modus) als auch außerhalb (nämlich im Normalmodus) über den Bildschirm geistern — anscheinend dabei allen bisher gelernten Regeln über die Grafik widersprechen. Wir werden in dieser Folge zwar lernen, mit ihnen umzugehen, sogar sie zu beherrschen — aber ihre genaue Funktion und Herkunft wird weiterhin im dunkeln bleiben: Meines Wissens gibt es noch kein Listing des Spriteunterstützenden Maschinenprogramms, das wohl im tiefsten Dunkel des VIC-II-Chip verborgen liegt: Denn der VIC-II-Chip belegt ja die Speicherplätze 53248 bis 54271. Im erreichbaren Teil dieses Zauberschlosses (53248 bis 53294) liegen die bisher viel von uns begangenen 47 Register (siehe 1. Folge, Tabelle 1), aber wo ist die Geheimtür zu den anderen 978 Bytes? Alles recht romantisch, werden Sie sagen. Nun — ganz so mysteriös ist die Sache nun auch wieder nicht, wie uns der Name Sprite = Kobold, Gespenst einreden will. Gehörig entschleiert wird das Geheimnis schon durch den anderen englischen Ausdruck für diese Dinger: MOBs. Das bedeutet: Movable Object Blocks, also bewegliche Blöcke von Objekten (Bildern, Darstellungen). Sie werden sehen, wenn wir mit dem MOBs umgehen können, ist das verbleibende Geheimnis eigentlich keines mehr, sondern verwandelt sich nur noch in eine Herausforderung für einen Maschinensprache-Programmierer.
Wir werden zunächst einmal schöpferisch tätig und erschaffen ein Sprite. Der erste Schritt dazu ist kreativ: Wie soll das Ding aussehen? Da bietet sich ja zum Beispiel der aus der Magie bekannte Drudenfuß an, auch Pentagramm genannt, weil wir ja schließlich diese Sprite-Geister bannen wollen (siehe Bild 1).

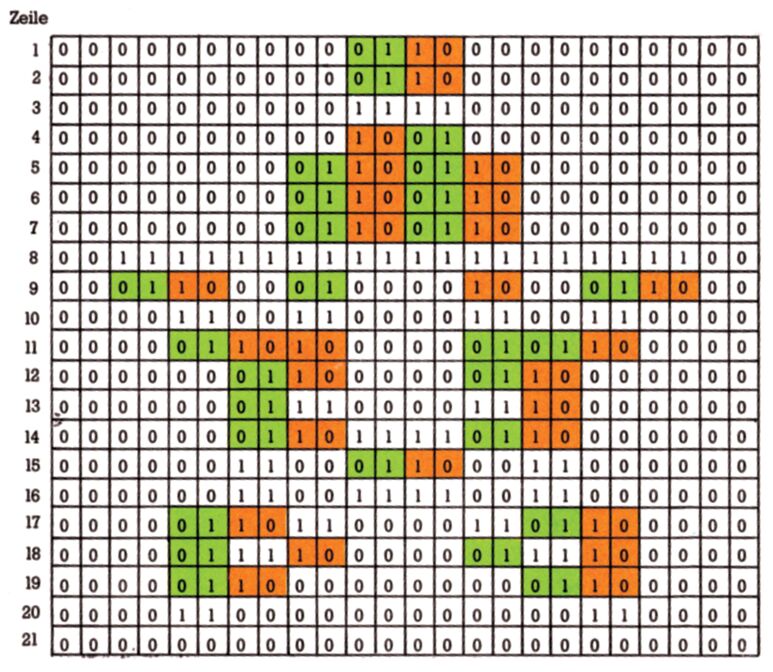
Jetzt müssen wir diese Zeichnung in eine Form bringen, die unser Computer versteht, also in Bytes. Wie auch schon bei den Buchstaben und der hochauflösenden Grafik sind hier wieder gesetzte und gelöschte Bits in den Bytes die Anzeige für »Punkt sichtbar« oder »Punkt nicht sichtbar«. Das im VIC-II-Chip organisierte Sprite-Programm nimmt die Bytes in der im Bild 2 gezeigten Anordnung wahr.
| Abschnitt 1 | Abschnitt 2 | Abschnitt 3 | |
| Zeile 1 | Byte 0 | Byte 1 | Byte 2 |
| Zeile 2 | Byte 3 | Byte 4 | Byte 5 |
| ⋮ | ⋮ | ⋮ | ⋮ |
| Zeile 20 | Byte 57 | Byte 58 | Byte 59 |
| Zeile 21 | Byte 60 | Byte 61 | Byte 62 |
Den so gebildeten Block verwaltet es in genau dieser Anordnung als ein Sprite. Deswegen müssen wir uns nun die Mühe machen, unser Pentagramm in so ein Bit-Raster einzufügen. Das ist in Bild 3 geschehen.

Nun muß dieses Bild in einen Zahlencode übersetzt werden. Überall dort, wo ein Bitfeld ausgefüllt ist, steht bei der Binärzahl eine 1, sonst eine Null. Demnach ergeben sich die Kennzahlen in der Tabelle 1.
| Zeile | Byte | binär | dez. |
| 1 | 0 1 2 |
00000000 00011000 00000000 |
4 24 0 |
| 2 | 3 4 5 |
00000000 00011000 00000000 |
0 24 0 |
| 3 | 6 7 8 |
00000000 00111100 00000000 |
0 60 0 |
| 4 | 9 10 11 |
00000000 00100100 00000000 |
0 36 0 |
| 5 | 12 13 14 |
00000000 01100110 00000000 |
0 102 0 |
| 6 | 15 16 17 |
00000000 01100110 00000000 |
0 102 0 |
| 7 | 18 19 20 |
00000000 01100110 00000000 |
0 102 0 |
| 8 | 21 22 23 |
00111111 11111111 11111100 |
63 255 252 |
| 9 | 24 25 26 |
00011000 01000010 00011000 |
24 66 24 |
| 10 | 27 28 29 |
00001100 11000011 00110000 |
12 195 48 |
| 11 | 30 31 32 |
00000110 10000001 01100000 |
6 129 96 |
| 12 | 33 34 35 |
00000001 10000001 10000000 |
1 129 128 |
| 13 | 36 37 38 |
00000001 11000011 10000000 |
1 195 128 |
| 14 | 39 40 41 |
00000001 10111101 10000000 |
1 189 128 |
| 15 | 42 43 44 |
00000011 00011000 11000000 |
3 24 192 |
| 16 | 45 46 47 |
00000011 00111100 11000000 |
3 60 192 |
| 17 | 48 49 50 |
00000110 11000011 01100000 |
6 195 96 |
| 18 | 51 52 53 |
00000111 10000001 11100000 |
7 129 224 |
| 19 | 54 55 56 |
00000110 00000000 01100000 |
6 0 96 |
| 20 | 57 58 59 |
00001100 00000000 00110000 |
12 0 48 |
| 21 | 60 61 62 |
00000000 00000000 00000000 |
0 0 0 |
Dieser Wust an Zahlen legt also unser Sprite fest. Diese doch recht aufwendige Rechnerei und Planerei ist, wenn sie aufmerkamer Leser von Computerliteratur sind — meist nicht mehr nötig. Obwohl es sicher gut ist, das Planen eines MOBs auch von Hand zu beherrschen (wie wir jetzt!), kann man sich die Arbeit doch mächtig erleichtern durch Eintippen eines der vielen Sprite-Editor-Programme, die es in fast allen Fachzeitschriften wie Sand am Meer gibt. Weil hier nicht der 1001. Sprite-Editor abgedruckt werden soll, dient das anliegende Programm »Sprity« anderen Zwecken. (Ein nettes kurzes Listing von H. Kunz finden Sie zum Beispiel in der Zeitschrift Computer persönlich Nr. 21, 1983 auf Seite 120). Jetzt müssen wir noch dafür sorgen, daß der C 64 diese Zahlen irgendwo zugreifbar hat, mit anderen Worten: Sie müssen in den Speicher gePOKEd werden. Im allgemeinen verwendet man dazu eine kleine FOR-NEXT-Schleife in der die in DATA-Zeilen abgelegten Zahlen gelesen und eingePOKEd werden. Wohin packt man die Kennzahlen? Im Prinzip kann man sie überall — wo sie nicht gerade lebenswichtige Computerfunktionen oder Basicprogramme stören — unterbringen. Es gibt lediglich zwei Dinge, die zu beachten sind:
a) Die Startadresse muß durch 64 glatt teilbar sein. (Zum Beispiel 896 = 14 mal 64 etc.)
b) Aus Gründen, auf die wir noch zu sprechen kommen werden, sollten die Sprite-Daten im gleichen 16 KByte-Speicherabschnitt (siehe vorangegangene Folge) abgelegt werden, in dem sich das Video-RAM befindet, welches bei der Sprite-Nutzung angeschaltet ist.
Damit gibt es im Prinzip 256 Orte pro Speicherabschnitt, in denen die Sprite-Daten gespeichert werden können. Allerdings sind einige Stellen zum Beispiel im Abschnitt 0 (mit dem normalen Bildschirm) bei der Verwendung von nur wenigen Sprites besonders bevorzugt, weil man keinen Basicspeicher wegnimmt und deshalb auch keine Schutz-POKEs nötig sind:
1) 704 — 767 ungenutzte Adressen
2) 832 — 895 Kassettenpuffer
3) 896 — 959 Kassettenpuffer
4) 960 — 1023 restlicher Kassettenpuffer und freier Platz.
Für weitere MOBs muß dann Basicspeicher verwendet und dieser dann vor dem Überschreiben durch Programmtext, Variablen oder Strings — wie in Folge 2 gezeigt — geschützt werden. Dem Erfindungsreichtum sind allerdings keine Grenzen gesetzt. So könnte man beispielsweise (siehe vorangegangene Folge) den Bildschirm an den oberen Rand des Abschnittes 2 verschieben und darunter oder darüber Sprite-Daten ablegen. Man muß dann zwar auch den Speicherschutz einPOKEn, hat aber trotzdem meistens noch mehr als genug Basicspeicherplatz. Wenn man nur vier Sprites gleichzeitig verwendet, insgesamt aber mehrere definiert hat, kann man sie alle im 4 KByte-Bereich ab $C000 abspeichern und bei Bedarf den Sprite, der dran ist, mit einer kleinen FOR-NEXT-Schleife in einen der vier Speicherbereiche (704 …. und so weiter) umladen. Sicher fallen Ihnen noch mehr Möglichkeiten ein. Wir werden uns im nachfolgenden einfach mit drei Sprites begnügen und uns nur im normalen Abschnitt 0 bewegen.
Legen wir also nun zunächst unser Pentagramm in den Bereich 704 bis 767 und nach 832 bis 895:
10 FOR I = 0 TO 62:READ A:POKE 704 + I,A:POKE 832 + I,A:NEXT I
30 DATA hier werden jetzt unsere 63 Kennzahlen eingegeben.
bis 60 DATA
Noch ignoriert der C 64 unsere Sprites völlig. Es interessiert ihn überhaupt nicht, was wir an Arbeit zum Füllen seiner Speicherbauches aufgewendet haben. Wir müssen ihm noch mitteilen, wo der VIC-II-Chip die Sprite-Daten finden kann. Weil dieser Chip dazu eingerichtet ist, gleichzeitig 8 MOBs zu verwalten, gibt es acht Speicherzellen, die sogenannte Sprite-Zeiger enthalten.
Na, wo ist er denn? Sprite-Zeiger
Sie befinden sich immer im gleichen 1 KByte-Bereich, in dem auch der Bildschirmspeicher liegt. Weil dieser Video-RAM nur 1000 Bytes benötigt, sind oberhalb desselben noch 24 Bytes frei, von denen die obersten 8 als Sprite-Zeiger dienen. Wenn also im Normalfall der Bildschirmspeicher von 1024 bis 2023 geht, dann liegen die Sprite-Zeiger von 2040 bis 2047. Verschiebt man den Bildschirm, dann werden die Sprite-Zeiger mit verschoben. In diese Sprite-Zeiger-Bytes POKEn wir die Zahlen ein, die mit 64 multipliziert die Startadresse der Sprite-Daten ergeben. In unserem Beispiel also: 704/64 = 11 und 832/64 = 13.
Wenn wir diese Sprite-Zeiger eingeben, nehmen wir automatisch gleichzeitig auch die Numerierung vor. Dabei gehört zu
Sprite Nr. 0 der Sprite-Zeiger 2040
Sprite Nr. 1 der Sprite-Zeiger 2041
Sprite Nr. 2 der Sprite-Zeiger 2042
und so weiter.
Nennen wir also einfach den Sprite, dessen Daten von 704 bis 767 liegen, Nummer 0 und den anderen Nummer 1, dann müssen wir also eingeben:
70 POKE 2040,11:POKE 2041,13
Damit sind die Sprite-Zeiger gesetzt.
Anschalten der Sprites
Wenn Sie jetzt freudig RUN (RETURN) eingetippt haben, um unsere Drudenfüsse zu sehen, werden Sie ein langes Gesicht gemacht haben: Nix zu sehen! Aber das ist wie bei einer Lampe: Sie haben den Lampenschirm, die Glühbirne, den Stecker eingesteckt und sie leuchtet nicht! Deswegen schalten wir sie jetzt ein, die Sprites. Der Schalter dafür sitzt im Sprite-Kontrollregister 53269 (siehe Folge 1 Tabelle der VIC-II-Chip-Register). Dort gibt es für jedes MOB ein Bit. Also Sprite Nummer 0 entspricht Bit Nummer 0 und so weiter. Ein Sprite ist eingeschaltet, wenn sein Bit auf 1 gesetzt ist. Wie man einzelne Bits setzt oder löscht, kennen wir noch aus der zweiten Folge. Spielen wir das hier nochmal an unserem Beispiel durch: Wir wollen Sprite Nummer 0 und Sprite Nummer 1 einschalten, müssen also die Bits 0 und 1 auf den Wert 1 setzen. Da gab es doch die OR-Funktion und eine sogenannte Maske:
XXXXXXXX irgendein binärer Inhalt von 53269
OR 00000011 Maske (= dezimal 3)
XXXXXX11 Ergebnis (Bits 0 und 1 sind = 1)
Das ergäbe die Programmzeile:
80 POKE 53269,PEEK(53269) OR 3
Will man einzelne MOBs mit der Nummer N einschalten, dann empfiehlt sich folgender Befehl:
POKE 53269,PEEK(53269) OR (2↑N)
Das Ausschalten geschieht durch die AND-Funktion. Jedes Bit, das mit 0 AND-verknüpft wird, wird dadurch gelöscht. Wenn wir also Sprite Nummer 1 ausschalten wollen, verwenden wir wieder eine Maske:
XXXXXX11 PEEK(53269), Sprite 0 und 1 eingeschaltet
AND 11111101 Maske (dezimal = 253)
XXXXXX01 Ergebnis: Bit 1 = 0, Sprite 1 ausgeschaltet,
Bit 0 = 1, Sprite 0 eingeschaltet.
Allgemein kann man einzelne Sprites also abschalten mit POKE 53269, PEEK(53269) AND (255-2↑N), wobei wieder N die Sprite-Nummer ist.
Ach, Ihre Geduld wird schon auf eine harte Probe gestellt. Wenn Sie nämlich bis jetzt alle Programmzeilen brav eingegeben und gestartet haben, sehen Sie immer noch kein Sprite! Aber Sie müssen dem MOB noch sagen, wo er erscheinen soll!
Schon wieder ein Koordinatensystem: Ort der Sprites
Vor den Erfolg haben auch die Commodore-Softwareplaner den Schweiß gesetzt! Denn nicht genug damit, daß wir den Bildschirm schon im Normalmodus in X-Richtung, in Y-Richtung in 25 Positionen und im Bit-Map-Modus in X-Richtung in 320, in Y-Richtung in 200 Positionen aufgeteilt finden, jetzt kommt noch eine Einteilung, die sogar noch über den sichtbaren Bildschirm hinausreicht! In Bild 4 sehen wir diese Aufteilung in 512 horizontale und 256 vertikale Koordinaten.
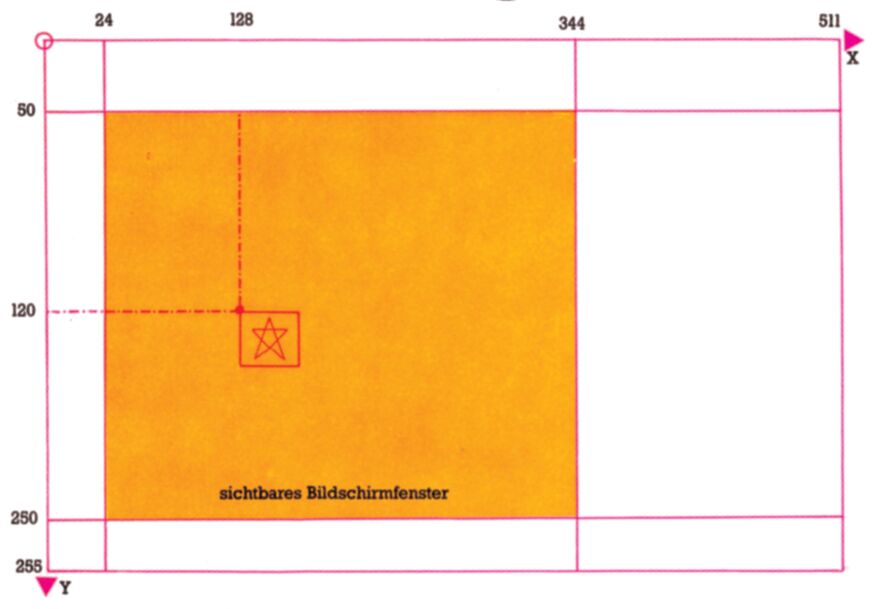
Für den Ort eines Sprites ist — wie in Bild angedeutet — die linke obere Ecke des Spritedefinitionsfeldes entscheidend. Also auch dann, wenn diese Ecke (wie in unserem Pentagramm) unsichtbar. So hat das im Bild gezeigte MOB die X-Koordinate 128 und die Y-Koordinate 120. Diese X-und Y-Werte muß man nun in die zur Sprite-Nummer gehörigen Register einPOKEn. Dabei handelt es sich um folgende Speicherstellen:
X-Position von Sprite 0 : 53248
Y-Position von Sprite 0 : 53249
X-Position von Sprite 1 : 53250
Y-Position von Sprite 1 : 53251
und so weiter bis
X-Position von Sprite 7 : 53262
Y-Position von Sprite 7 : 53263
Um nun also endlich unser Sprite Nummer 0 sichtbar zu machen, geben wir ein:
100 POKE 53248,128:POKE 53249,120
So! Jetzt tippen Sie ein RUN (RETURN) und endlich: Da ist unser Pentagramm. Gefällt es Ihnen? Sprite 1, das zweite Pentagramm, soll am rechten Bildschirmrand auftauchen, also ungefähr bei X = 266 und bei Y = 130. Deswegen müßten wir aber in die entsprechende X-Positions-Speicherstelle für Sprite 1 eine Zahl größer als 255 einPOKEn! Wenn Sie’s versuchen, meldet der Computer natürlich einen ILLEGAL QUANTITY ERROR. Geht also nicht! Anscheinend war das bisher noch nicht verzwickt genug. Jetzt müssen wir nämlich mal wieder das Hexadezimalsystem bemühen (die Sechzehnfingerlinge, erinnern Sie sich: Folge 2).
Dezimal 266 ist hexadezimal $010A. Jetzt zerteilen wir diese Zahl wieder in das LSB und das MSB:
| $01 | 0A |
| MSB | LSB |
| =1 | =0A |
und rechnen wieder zurück ins Dezimalsystem:
MSB = 1
LSB = 10
Rechnen Sie mal nach: Das MSB kann auch bei der höchsten X-Position nie größer als 1 werden. Es gibt also nur zwei Fälle: Ist die X-Position größer als 256, dann ist das MSB 1, sonst ist es 0.
Deswegen speichert man die MSBs aller 8 Sprites in nur einem Byte. Ebenso wie beim Kontrollregister für das An- und Ausschalten gehört auch hier zu jedem Sprite ein Bit, also: Bit 1 gehört zu Sprite 1 und so weiter. Wenn nun also die X-Koordinate von Sprite 1 266 ist, dann ergibt die Aufspaltung, wie oben gezeigt, MSB = 1 und LSB = 10. Das Register für die MSBs ist Speicherstelle 53264. Die 10 (das LSB) wird also in die normale Speicherstelle für die X-Position gePOKEt. Das MSB ( = 1 ) ist also Bit 1 (weil Sprite 1) von Speicherstelle 53264. Hier ist also wieder eine OR-Operation nötig. Die Y-Position wird ganz normal eingegeben. Es ergibt sich also die Programmzeile:
110 POKE 53250,10:POKE 53264, PEEK(53264)OR(2↑l):
POKE 53251,130
Wenn Sie jetzt einen Schwarzweiß-Monitor haben, sehen Sie nach RUN (RETURN) trotzdem nur unser Sprite Nummer 0. Farbmonitor-Eigner bewundern schon jetzt Sprite Nummer 1. Warum, das wird uns gleich noch beschäftigen.
Welche Koordinaten eines Sprites sind eigentlich möglich, und was sieht man dann? Um das zu erforschen, bauen wir uns ein Primitiv-Sprite:
20 FOR I = 0TO 62:POKE I+896, 255:NEXT I:POKE 2042,14:
REM SPRITE NR. 2
Dann schalten wir ein:
90 POKE 53269,PEEK(53269) OR (↑2)
und bauen eine Abfrage ein für die Position:
130 INPUT"SPRITE 2:X,Y=";X,Y:IF X=-1THENEND
Für die X-Position soll der Computer noch die Umrechnung in LSB und MSB für uns durchführen:
140 X1=INT(X/256):X2 = X-256*X1
Dann POKEn wir diese Koordinaten ein:
150 POKE 53252,X2:POKE 5253,Y:
IF X1=1 THEN POKE 53264,PEEK (53264)OR(2↑2)
Wenn die X-Koordinaten kleiner als 256 sind, also das MSB = 0 ist, muß es natürlich gelöscht werden:
160 IF X1=0 THEN POKE 53264,PEEK(53264)AND(255-2↑27)
Schließlich lassen wir uns außer dem Sprite Nummer 2 auch noch die eingegebenen Koordinaten zeigen und kehren zur Abfrage zurück:
170PRINTCHR$(147), "x = "x, "y = "y: GOTO 130
Wenn Sie jetzt starten, können Sie alle möglichen Positionen für X und Y eingeben. Versuchen Sie doch mal X = 265, Y = 130. Da ist auch für die Schwarzweiß-Seher (ich bin auch einer) unser Sprite Nummer 1 zu erkennen. Warum, dazu kommen wir noch. Wenn Sie genug ausprobiert haben, dann geben Sie für X jetzt -1 und irgendeinen Y-Wert ein und das Programm ist beendet. Vermutlich haben auch Sie festgestellt, daß man unseren Testsprite ganz allmählich über den sichtbaren Bildschirmrand hinauswandern lassen kann. Es ergeben sich so die Grenzkoordinaten in Tabelle 2:
| Sprite gerade noch voll sichtbar | Sprite gerade nicht mehr sichtbar | ||
|---|---|---|---|
| links oben | rechts oben | links oben | rechts oben |
| X = 24 Y = 50 |
X = 320 Y = 50 |
X = 0 oder/und Y = 29 |
X = 344 oder/und Y = 29 |
| links unten | rechts unten | links unten | rechts unten |
| X = 24 Y = 229 |
X = 320 Y = 229 |
X = 0 oder/und Y = 250 |
X = 344 oder/und Y = 250 |
Die in der Tabelle 2 angegebenen Werte gelten allerdings nur für die normalen Sprites. Also gibt es auch noch anormale Sprites? Ja, die gibt’s auch. Aber wir wollen der Reihe nach vorgehen. Wir können jetzt Sprites entwerfen, Sprite-Zeiger setzen, MOBs an- und wieder abschalten und sie an die richtige Stelle setzen.
Mal wieder Farbe: Diesmal die von Sprites.
Eines haben wir bisher total vergessen: Welche Farbe soll unser Sprite haben und wie geben wir sie ihm? Auch hierfür gibt es natürlich wieder Register, die Sprite-Farben-Register und zwar die in der Tabelle 3.
| Sprite No. | Register |
| 0 | 53 287 |
| 1 | 53 288 |
| 2 | 53 289 |
| ⋮ | ⋮ |
| 7 | 53 294 |
In diese Register POKEt man die Farbe (Kennzahlen 0 bis 15) ein, in der der MOB erscheinen soll. Testen Sie mal: Ändern wir Zeile 130. Dort soll in der IF-THEN-Anweisung nach THEN anstelle von END jetzt stehen 180. Diese Zeile 180 schaltet das vorerst ausgediente Sprite 2 aus:
180 POKE 53269,PEEK(53269) AND (255-2↑2)
Damit eröffnen wir uns die Farbeingabemöglichkeit mit:
190 PRINT CHR$(147):INPUT"SPRITE 0,SPRITE 1 FARBEN";
F1,F2:IF F1=-1THEN210
Schließlich POKEn wir die Farben in die zu den Sprites gehörigen Register:
200 POKE 53287,F1:POKE53288,F2:GOTO190
210 END
Jetzt können Sie, bis Sie schließlich für F1 mal -1 eingeben, allerlei Farben durchprobieren. Wir erkennen nun auch, daß bislang Sprite 1 für Schwarzweiß-Seher nicht erkennbar war, weil seine Farbe keinen Kontrast zur Hintergrundfarbe gebildet hat.
Wem’s noch nicht bunt genug war bisher, der hat auch hier bei den Sprites die Möglichkeit, den Mehrfarben-Modus zu verwenden. Während im bisher gebrauchten Modus jedes Sprite-Definitions-Bit entweder 0 (= Hintergrundfarbe oder 1 (Farbe des zum Sprite gehörigen Sprite-Farb-Registers) sein konnte, zählen - wie auch sonst im Mehrfarbenmodus - wieder Bit-Paare. Dabei stammt dann die jeweilige Farbe aus den in Tabelle 4 angegebenen Registern.
| Bit-Paar | Farbherkunft |
| 00 | durchsichtig |
| 01 | Sprite Mehrfarbregister 53 285 |
| 10 | normale Sprite-Farben-Register (53 287 bis 53 294) |
| 11 | Sprite Merhfarbregister 52 286 |
Unser Drudenfuß sieht somit dann aus wie in Bild 5 gezeigt.
Das wollen wir noch einmal auf dem Bildschirm ansehen. Wir schreiben ab Zeile 190 neu:
190 PRINT CHR$(147):INPUT"MOB1,MOB2,MULTCOL1,MULTCOL2";F1,F2,F3,F4:IFF1=—1THEN 220
200 POKE 53287,F1:POKE53288,F2:POKE 53285,F3:POKE 53286,F4
220 END
So läuft natürlich noch nichts Neues, denn der Mehrfarben-Modus muß noch angeschaltet werden. Auch dazu gibt es wieder ein Register: 53276. Wie bei einigen anderen Sprite-Registern gehört auch wieder zu jedem MOB das entsprechende Bit, also zu Sprite 1 das Bit 1 und so weiter. Wenn dieses Bit auf 1 gesetzt ist, ist für das dazugehörige
Sprite der Mehrfarb-Modus angeschaltet. Man kann sie also einzeln oder zusammen - ganz wie’s beliebt - im Normal-Modus oder im Muticolor-Modus betrachten. Wir schalten Sprite 0 und Sprite 1 in den Mehrfarb-Modus mit Zeile
210 POKE 53276,PEEK(53276)OR3:GOTO 190
Will man nur Sprite Nummer N umschalten, dann verwendet man wie gehabt: POKE 53276, PEEK(53276)OR(2↑N).
Das Zurückschalten in den Normalmodus geschieht dann durch Löschen der entsprechenden Bits:
POKE 53276,PEEK(53276)AND (255-2↑N).
Auch hier habe ich das Programm so gebaut, daß man durch Eingabe von -1 und irgendwelchen drei anderen Zahlen aussteigen kann. Im Verlauf des Probierens werden Sie bestimmt gemerkt haben, daß man Sprites, die für den Mehrfarben-Modus gedacht sind, speziell konstruieren sollte unter Berücksichtigung der Bit-Paar-Zusammenstellungen. Unser Drudenfuß gefällt mir im Normal-Modus jedenfalls besser.
Deswegen schalten wir in Zeile 220 lieber den Mehrfarben-Modus aus:
220 POKE 53276,PEEK(53276) AND 252
Anormale Sprites? Gequetschte und gezerrte MOBS
Die normalen Sprites bestehen aus 24 x 21 Bildpunkten und haben auf dem Bildschirm eine Ausdehnung von zirka drei Zeilen mal drei Spalten. Für einige Effekte ist es ganz nett, sie in ihrer Größe verändern zu können. Genau das ist möglich, und zwar in X-Richtung, in Y-Richtung oder in beide Richtungen gleichzeitig. Das Merkwürdige an diese Sache ist - außer dem manchmal recht verzerrten Aussehen -, daß die gleiche 24 mal 21 Pixel abgebildet werden, nur jedes Pixel ist vergrößert. Wenn sowohl in X-als auch in Y-Richtung vergrößert wurde, ist einfach jeder Bildpunkt viermal so groß wie vorher. Auch hier geschieht das natürlich wieder über Kontrollregister, von denen jedes Bit wieder zu einem Sprite gleicher Nummer gehört. Die Verdoppelung in X-Richtung wird durch eine 1 im zum Sprite gehörigen Bit des Registers 53277, die in Y-Richtung auf die gleiche Weise im Register 53271 geschaltet. Wenn wir also unser Sprite Nummer 0 in X-Richtung verdoppeln wollen, dann geben wir noch ein:
230 POKE 53277,PEEK(53277)OR1:FOR I=0TO2000:NEXT I
Dann sehen wir uns das nach einer kleinen Pause noch in Y-Richtung an:
240 POKE 53277,PEEK(53277)AND 254:POKE53271,PEEK(53271)OR1:FORI=O TO 2000:NEXT I
Jetzt vergrößern wir noch in beide Richtungen:
250 POKE 53277,PEEK(53277) OR 1
Wie Sie sich denken können, stimmt jetzt die Positionierung dieser vergrößerten Sprites auf dem sichtbaren Bildschirmteil nicht mehr. Um das zu testen, bemühen wir wieder unser Testsprite Nummer 2 und vergrößern in beide Richtungen:
120 POKE 53277,PEEK(53277)OR4:POKE53271,PEEK(53271)OR4
Wenn wir nun das Programm mit RUN (RETURN) starten, taucht unser Test-Sprite in vergrößterter Form auf und wir können es wieder an verschiedene Orte auf dem Bildschirm packen. Für dieses in beide Richtungen verdoppelte MOB findet man dann die Grenzwerte in Tabelle 5.
| Sprite gerade noch voll sichtbar | Sprite gerade nicht mehr sichtbar | ||
|---|---|---|---|
| links oben | rechts oben | links oben | rechts oben |
| X = 24 Y = 50 |
X = 296 Y = 50 |
X nicht möglich nur: Y = 8 |
X = 344 oder/und Y = 8 |
| links unten | rechts unten | links unten | rechts unten |
| X = 24 Y = 208 |
X = 926 Y = 208 |
X nicht möglich nur: Y = 250 |
X = 344 oder/und Y = 250 |
Will man also ein solchermaßen vergrößertes Sprite langsam aus dem Bildschirm ziehen lassen, dann ist das nicht nach links möglich, weil selbst bei X = 0 der Sprite noch teilweise sichtbar ist.
Jetzt wissen wir eigentlich fast alles, was mit dem einzelnen Sprite zusammenhängt. Wenn Sie ein sich veränderndes Sprite darstellen wollen, so ist das zum Beispiel möglich, indem alle zu zeigenden Bewegungsphasen als Spritemuster im Speicher abgelegt werden und dann per Programm der Sprite-Zeiger auf den jeweils aktuellen Bewegungszustand umgeschaltet wird. So könnte man wie in Bild 6 die Abläufe A bis G im Speicher ablegen und zum Beispiel den Sprite-Zeiger für Sprite 3 zuerst auf das Muster A, dann nach entsprechender Verzögerung auf Muster B, dann C, D, E, F, G und schließlich wieder A richten. Wenn die einzelnen Spritemuster gut gemacht und die Verzögerungsschleifen richtig abgestimmt sind, kann so eine Art Zeichentrickfilm ablaufen, der nun auch noch durch die anderen bisher gelernten Sprite-Eigenheiten (Vergrößern, Position, Farbe etc.) veränderbar ist. Wie Sie unschwer erkennen, sind Ihrer Phantasie keine Grenzen gesetzt, und ich würde mich freuen, von Ihnen mal so einen witzigen Trickablauf sehen zu können. Auf einem ähnlichen Prinzip basiert auch ein Programm von Hans Grigat in Happy-Computer, Ausgabe Nummer 11 (1983), Seite 99 ff. Überhaupt lohnt es sich, sich dieses Programm mal genau anzusehen, weil hier die anfangs erwähnte Möglichkeit der Sprite-Daten-Verschiebung genutzt wurde.
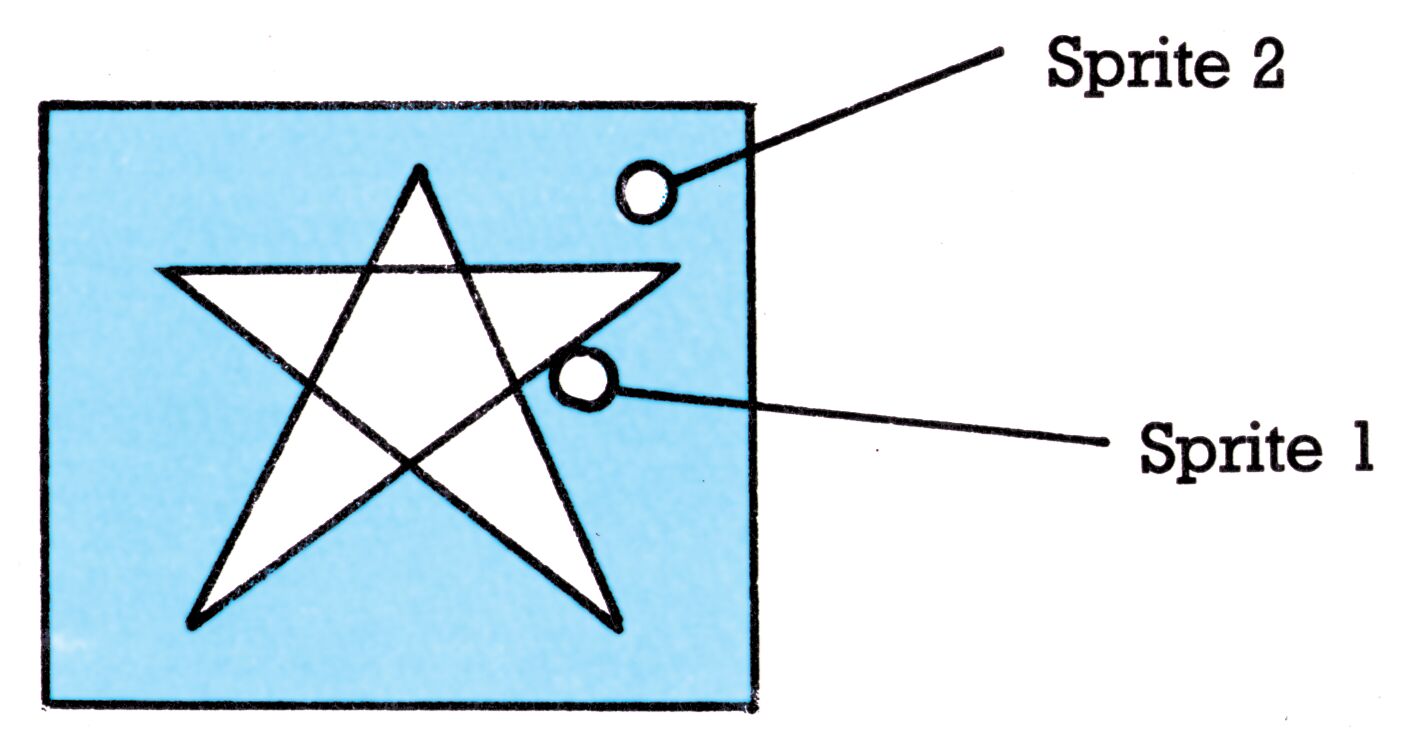
Wer hat Vorfahrt? Prioritäten
Wir wollen uns jetzt noch um die Beziehung von Sprites zu ihrer Umwelt (also zu anderen Sprites und/oder zu Zeichen auf dem Bildschirm) kümmern. Sie erinnern sich vielleicht an unseren Versuch, unser kleines Test-Sprite über den Bildschirm zu bewegen und an ein Ergebnis davon, nämlich, daß auch Schwarzweiß-Sehern plötzlich bei Eingabe der abgedruckten Bildschirmposition das Sprite Nummer 1 sichtbar war. Wenn also — wie in diesem Fall — zwei Sprites sich überdecken, welches von beiden wird dann gezeigt? Siehe dazu das Bild 7, auf dem die Situation abgebildet ist. Wir sehen da: an den Stellen, wo Sprite 1 Bits mit dem Wert 0 vorliegen hat, ist Sprite 2 zu sehen. Wo aber der Bitwert des Sprite 1 gleich 1 ist, wird Sprite 2 durch Sprite 1 verdeckt. Das MOB 1 hat eine höhere Priorität als MOB 2. Der VIC-II-Chip organisiert die Prioritäten von Sprites untereinander also in folgender Weise: Höchste Priorität hat Sprite 0, dann folgt Sprite 1, Sprite 2 und so weiter bis zum Schlußlicht Sprite 7.
Wenn Sie also Programme planen, in denen Sprites aneinander vorbeiziehen sollen, denken Sie daran, daß an diese Vorfahrtsregelung nichts zu ändern ist. Unter Umständen muß man dann die Sprite-Zeiger umwechseln, um die Prioritäten umzukehren: Man macht dann beispielsweise für den Augenblick der Überschneidung aus Sprite 7 zum Beispiel Sprite 1 und umgekehrt.
Eine andere Vorfahrtsregelung gilt, wenn Sprites und Bildschirmzeilen (oder Bit-Map-Darstellungen) aufeinandertreffen. Hier haben wir ein Kontrollregister zur Hand (mal wieder eines!), Speicherstelle 53275, wo wieder jedem Sprite ein Bit entspricht (also Bit 0 entspricht Sprite 0 und so weiter). Wenn nun dieses Bit den Wert 0 hat, steht das dazugehörige MOB vor den Bildschirmdarstellungen, andernfalls verkrümelt es sich dahinter.
Das wollen wir uns mal ansehen! Starten Sie das Programm nochmal und wenn Sie an die Farbabfrage kommen, geben Sie dem Sprite 0 die Farbe 0 (= schwarz). Beenden Sie das Programm in der angegebenen Weise und wenn sich READY gemeldet hat. LISTen Sie das ganze. Jetzt steht unser schwarzes Pentagramm vor dem Listing. Geben sie nun im Direktmodus ein:
POKE 53275,1 (RETURN). Siehe da: Sprite 0 versteckt sich hinter dem Listing.
Wir können also zusammenfassen: Überall dort, wo auf dem Bildschirm (durch Buchstaben oder andere Zeichen) ein Bit gesetzt ist, verschwindet dahinter ein gegebenenfalls vorhandener Sprite-Bildpunkt (wenn natürlich das zum Sprite gehörige Bit im Register 53275 gesetzt ist). Nur dort, wo auf dem Bildschirm ein Bit nicht gesetzt ist (also 0 ist), sieht man einen dort vorhandenen Sprite-Bildpunkt.
Etwas komplizierter liegen die Verhältnisse, wenn wir das MOB im Mehrfarben-Modus vorliegen haben. Hier werden nämlich auch Bildschirmbitpaare 01 (von Zeichen oder Bit-Map-Darstellungen) genauso behandelt wie Bitpaare 00. Das heißt, auch an solchen Stellen wird ein eventuell vorhandenes Sprite-Bitpaar dargestellt.
Zusammenstöße: Kollisionsregister
Erfreulicherweise haben die Software-Planer des C 64 auch zwei Möglichkeiten vorgesehen, Zusammenstöße in Registern abzufragen. Weil es zwei Sorten von Zusammenstöße gibt (Sprite kollidiert mit Sprite und Sprite kollidiert mit Zeichen), kann man zwei Register abfragen.
Da hätten wir zunächst das Sprite-Sprite-Kollisions-Register 53278. Auch hier gehört zu jedem Bit ein Sprite, wie bei den anderen Kontroll-Registern. Von einem Zusammenstoß spricht man in Sprite-Kreisen immer dann, wenn undurchsichtige Teile der MOBs aufeinandertreffen. Überlappen sich nur die Teile, deren Bits bei der Sprite-Definition auf 0 gesetzt wurden, so zählt das nicht als Kollision. Die Bits der Sprites, die in den Zusammenstoß verwickelt sind, werden auf 1 gesetzt, zum Beispiel erzeugt ein Zusammenstoß von Sprite 0 mit Sprite 1 folgenden Inhalt des Registers 53278: 00000011 = dezimal 3.
Wenn in einem Supercrash acht Sprites kollidieren, steht im Sprite-Sprite-Kollisionsregister 255. Übrigens werden auch Zusammenstöße registriert, die außerhalb des sichtbaren Bildschirms liegen (siehe Bild 4).
Wenn ein Sprite mit Bildschirmdarstellungen (Zeichen und so weiter) zusammenstößt, wird in Register 53279 das zu ihm gehörende Bit gesetzt. Stößt also Sprite Nummer 1 mit zum Beispiel einem A zusammen, dann liest man aus dem Register 53279: 00000010 = dezimal 2. Apropos lesen: Die Register 53278 und 53279 sind so gestaltet, daß sie nach dem Herauslesen (PEEKen) gelöscht sind! Deswegen empfiehlt es sich, wenn man diese Inhalte danach noch braucht, sie in Variablen abzulegen. Auch bei dieser Sorte Zusammenstößen zählen nur diejenigen, bei denen undurchsichtige Sprite-Teile kollidieren. Wenn übrigens Bildschirminhalte horizontal aus dem sichtbaren Bereich »herausgescrollt« worden sind (zum »Scrollen« kommen wir in der nächsten Folge), und dabei ein Zusammenstoß mit einem Sprite geschieht, wird ebenfalls ein Bit in 53279 gesetzt.
Manfred Thoma hat das anliegende Programm »Sprity« geschrieben, mit dem Sie einige Sprite-Eigenschaften und die dazugehörigen Registerveränderungen beobachtet werden können.
Obwohl es zu den MOBs noch einiges zu sagen gäbe (wie kommen sie auf den Bildschirm, schnelles Steuern und so weiter), soll das Thema hiermit abgeschlossen sein. Ich denke, daß wir in dieser Folge die kleinen Kobolde schon weitgehend entzaubern konnten mit Hilfe unserer Pentagramme. Zu den Sprites gibt es mehr Literatur als zu vielen anderen C 64-Themen. Hier eine kleine Auswahl:
- Zwei Artikel wurden schon genannt (von H. Grigat und H. Kunz)
- Herbert Kunz hat auch schon etwas über schnelles Bewegen von MOBs geschrieben im 64’er, Ausgabe 4/83 auf Seite 70f.
- Einen Überblick vor allem über die Anwendung von Sprites in Spielen geben Schneider und Ebert in den Bänden 1 und 3 des Commodore 64-Buches. Erschienen 1984 in Haar bei München im Markt & Technik Verlag. Diese beiden Bände sind auch von den sehr gut überschaubaren Programmbeispielen her zu empfehlen.
10 : rem*********************************************************************
20 : rem** s p r i t y **
30 : rem** **
40 : rem** manfred walter thoma 2102 hamburg 93 ernastrasse 10 **
50 : rem** **
60 : rem*********************************************************************
70 poke53280,0:poke53281,0:poke646,1:printchr$(147);
75 : rem*********************************************************************
80 : rem** daten fuer die drei sprites **
90 : rem*********************************************************************
100 data0,0,0,0,0,0,0,0,0,0,0,0,0,14,0,0,17,0,0,32,128,0,64,64,0,155,32,0,128
110 data32,0,132,32,0,132,32,0,145,32,0,78,64,0,32,128,0,31,0,0,0,0,0,0,0,0,0
120 data0,0,0,0,0,0,0
130 data0,0,0,0,0,0,0,0,0,0,0,0,0,14,0,0,17,0,0,32,128,0,64,64,0,155,32,0,128
140 data32,0,132,32,0,132,32,0,128,32,0,78,64,0,64,64,0,32,128,0,31,0,0,0,0,0
150 data0,0,0,0,0,0,0,0
160 data0,0,0,0,0,0,0,0,0,0,0,0,0,14,0,0,17,0,0,32,128,0,64,64,0,155,32,0,128
170 data32,0,132,32,0,132,32,0,128,32,0,78,64,0,81,64,0,64,64,0,32,128,0,31,0
180 data0,0,0,0,0,0,0,0,0
190 : rem*********************************************************************
200 : rem** einlesen der sprites und titelbild **
210 : rem*********************************************************************
220 printtab(12)"s p r i t y"
230 printtab(12)"================"
240 print:print:print:print
250 printtab(19)"by"
260 printtab(12)"manfred w. thoma"
270 printtab(12)"2102 hamburg 93"
280 printtab(12)" ernastrasse 10"
290 fori=13*64to13*64+62:readx:pokei,x:next
300 poke2040,13: rem** sprite 0 aus block 13 **
310 fori=14*64to14*64+62:readx:pokei,x:next
320 poke2041,14: rem** sprite 1 aus block 14 **
330 fori=15*64to15*64+62:readx:pokei,x:next
340 poke2042,15: rem** sprite 2 aus block 15 **
350 v=53248: rem** startadresse des vic 2 chip**
360 poke v+39,1: rem** farbe fuer sprite 0 **
370 poke v+40,1: rem** farbe fuer sprite 1 **
380 poke v+41,1: rem** farbe fuer sprite 2 **
390 poke v+23,7: rem** sprites 0-2 in x-richtung **
400 poke v+29,7: rem** sprites 0-2 in y-richtung **
410 poke v,160:pokev+1,160: rem** x-y-koordinaten sprite 0 **
420 poke v+2,160:pokev+3,160: rem** x-y-koordinaten sprite 1 **
430 poke v+4,160:pokev+5,160: rem** x-y-koordinaten sprite 2 **
440 for i=1 to 10
450 pokev+21,1:for ii=1to300:next: rem** einschalten nur sprite 0 **
460 pokev+21,2:for ii=1to200:next: rem** einschalten nur sprite 1 **
470 pokev+21,4:for ii=1to100:next: rem** einschalten nur sprite 2 **
480 nexti
490 pokev+21,0: rem** ausschalten aller sprites **
500 printchr$(147)
510 dr$="{CBM-N} _{left}{left}{left}{left}{left}{left}"
520 poke 650,128: rem** repeat fuer alle tasten **
530 : rem*********************************************************************
540 : rem** tastenbelegungserklaerung **
550 : rem*********************************************************************
560 printchr$(147);
570 printtab(9)"bewegungssimulation"
580 printtab(9)"==================="
590 print:print"{CBM-A}CCCC{CBM-S}"
600 print"B f1 B bewegen sprite 0 in +x richtung";
610 print"{CBM-Q}CCCC{CBM-W}
620 print"B f3 B bewegen sprite 0 in -x richtung";
630 print"{CBM-Q}CCCC{CBM-W}
640 print"B f5 B bewegen sprite 0 in +y richtung";
650 print"{CBM-Q}CCCC{CBM-W}
660 print"B f7 B bewegen sprite 0 in -y richtung";
670 print"{CBM-Z}CCCC{CBM-X}
680 print:print"{CBM-A}CCCC{CBM-S}"
690 print"B f2 B bewegen sprite 1 in +x richtung";
700 print"{CBM-Q}CCCC{CBM-W}
710 print"B f4 B bewegen sprite 1 in -x richtung";
720 print"{CBM-Q}CCCC{CBM-W}
730 print"B f6 B bewegen sprite 1 in +y richtung";
740 print"{CBM-Q}CCCC{CBM-W}
750 print"B f8 B bewegen sprite 1 in -y richtung";
760 print"{CBM-Z}CCCC{CBM-X}
770 print:printtab(11)"weiter bitte taste"
780 geta$:ifa$=""then780
790 print"{clr}{rvon}verkleinern der sprite"
800 print"nach druecken der taste{rvon}< v >{rvof}kann mit den";
810 print"funktionstasten in +x,-x und +y,-y ver-";
820 print"kleinert werden."
830 print"{down}{rvon}farben
840 print"nach druecken der taste{rvon}< f >{rvof}kann mit der";
850 print"taste >f1< die farbe fuer sprite0 geaen-";
860 print"dert werden.mit >f2< farbe fuer sprite1.";
870 print"{rvon}{down}hintergrundfarbe"
880 print"duch druecken d. taste{rvon}< h >{rvof}wird die"
890 print"bildschirmfarbe geaendert."
900 print"{down}{rvon}ende"
910 print"programmende mit taste{rvon}< e >{rvof}"
920 print"{down}{rvon}sprite ein/aus"
930 print"nach druecken der taste{rvon}< o >{rvof}kann mit den";
940 print"funktionstasten >f1< und >f2<sprite0 und";
950 print"sprite1 ein- bzw. ausgeschaltet werden"
960 print"{down} {rvon}weiter bitte taste"
970 geta$:ifa$=""then970
980 print chr$(147);
990 printspc(33)"{CBM-N}{rvon}x-sp.0{rvof}";
1000 printspc(33)"{CBM-N} 50 _";
1010 printspc(33)"{CBM-N}{rvon}y-sp.0{rvof}";
1020 printspc(33)"{CBM-N} 150 _";
1030 printspc(33)"{CBM-N}{rvon}x-sp.1{rvof}";
1040 printspc(33)"{CBM-N} 150 _";
1050 printspc(33)"{CBM-N}{rvon}y-sp.1{rvof}";
1060 printspc(33)"{CBM-N} 150 _";
1070 printspc(33)"{CBM-N}{rvon}farbe0{rvof}";
1080 printspc(33)"{CBM-N} 1 _";
1090 printspc(33)"{CBM-N}{rvon}farbe1{rvof}";
1100 printspc(33)"{CBM-N} 1 _";
1110 printspc(33)"{CBM-N}{rvon}x-dehn{rvof}";
1120 printspc(33)"{CBM-N} 3 _";
1130 printspc(33)"{CBM-N}{rvon}y-dehn{rvof}";
1140 printspc(33)"{CBM-N} 3 _";
1150 printspc(33)"{CBM-N}{rvon}schirm{rvof}";
1160 printspc(33)"{CBM-N} 0 _";
1170 printspc(33)" {CBM-T}{CBM-T}{CBM-T}{CBM-T}{CBM-T}{CBM-T}";
1180 printspc(33)"{CBM-N}{rvon}on/off{rvof}";
1190 printspc(33)"{CBM-N}{rvon}s0:{rvof} on";
1200 printspc(33)"{CBM-N}{rvon}s1:{rvof} on";
1210 print"{rvon} s p r i t y ";chr$(19)
1220 pokev,50:
1230 pokev+2,150
1240 pokev+21,3
1250 a=peek(v+30): rem** lesen/loeschen kollisonreg**
1260 : rem*********************************************************************
1270 : rem** tastatur abfrage (get) **
1280 : rem*********************************************************************
1290 geta$:ifa$=""then1290
1300 if a$="e"thenprintchr$(147):pokev+21,0:end
1310 if a$="h"then 1730: rem** aendern der bilds.farbe **
1320 if a$="v"then 1990: rem** sprites kleiner/groesser **
1330 if a$="f"then 1830: rem** sprites farbe **
1340 if a$="o"then 2210: rem** sprites ein/aus **
1350 a=asc(a$)-132: rem** umrechnen funktionstasten **
1360 ifa<0 or a>8then1290: rem** keine funktionstaste **
1370 on a gosub 1490,1520,1550,1580,1610,1640,1670,1700
1380 : rem*********************************************************************
1390 : rem** kollisions abfrage **
1400 : rem*********************************************************************
1410 if peek(v+30)=0 then 1290
1420 print"{home} !!! kollision !!!"
1430 for i=0 to 100:next
1440 print"{home} "
1450 goto 1290
1460 : rem*********************************************************************
1470 : rem** sprite bewegen x/y-koord. **
1480 : rem*********************************************************************
1490 we=peek(v):ifwe=255 then return
1500 we=we+1:pokev,we
1510 z=1:gosub2370:return
1520 we=peek(v):ifwe=1then return
1530 we=we-1:pokev,we
1540 z=1:gosub2370:return
1550 we=peek(v+1):ifwe=1then return
1560 we=we-1:pokev+1,we
1570 z=3:gosub2370:return
1580 we=peek(v+1):ifwe=198then return
1590 we=we+1:pokev+1,we
1600 z=3:gosub2370:return
1610 we=peek(v+2):ifwe=255 then return
1620 we=we+1:pokev+2,we
1630 z=5:gosub2370:return
1640 we=peek(v+2):ifwe=1then return
1650 we=we-1:pokev+2,we
1660 z=5:gosub2370:return
1670 we=peek(v+3):ifwe=1then return
1680 we=we-1:pokev+3,we
1690 z=7:gosub2370:return
1700 we=peek(v+3):ifwe=198then return
1710 we=we+1:pokev+3,we
1720 z=7:gosub2370:return
1730 : rem*********************************************************************
1740 : rem** hintergrundfarbe (bilds.) **
1750 : rem*********************************************************************
1760 hf=peek(53280)
1770 if hf=255 then poke53280,0:poke53281,0:we=0:z=17:gosub2370:goto 1290
1780 poke53280,hf+1:poke53281,hf+1
1790 we=hf+1-240:z=17:gosub2370
1800 goto 1290
1810 :
1820 :
1830 : rem*********************************************************************
1840 : rem** sprite farben **
1850 : rem*********************************************************************
1860 for i=1 to50
1870 geta$
1880 ifa$=chr$(133) or a$=chr$(137)then 1910:rem** pruefen >f1< oder >f2< **
1890 next i
1900 goto 1290
1910 f1=peek(v+40):f2=peek(v+39): rem** aktuelle farben sprite 0+1**
1920 if a$=chr$(137) then 1960
1930 if f2=255then pokev+39,0:we=0:z=9:gosub2370:goto1290
1940 poke v+39,f2+1:we=f2+1-240:z=9:gosub2370
1950 goto1290
1960 if f1=255then pokev+40,0:we=0:z=11:gosub2370:goto1290
1970 poke v+40,f1+1:we=f1+1-240:z=11:gosub2370
1980 goto1290
1990 : rem*********************************************************************
2000 : rem** verkleinern der sprites **
2010 : rem*********************************************************************
2020 for i=1 to 100
2030 geta$:if a$=""then2060
2040 a=asc(a$)-132
2050 if a>0 and a<9 then 2070
2060 next i:goto1290
2070 dx=peek(v+29):dy=peek(v+23)
2080 on a goto 2100,2110,2120,2130,2140,2150,2160,2170
2090 goto1260
2100 dx=dx or 1:goto2180
2110 dx=dx and 254:goto2180
2120 dy=dy or 1:goto2190
2130 dy=dy and 254:goto2190
2140 dx=dx or 2:goto2180
2150 dx=dx and 253:goto2180
2160 dy=dy or 2:goto2190
2170 dy=dy and 253:goto2190
2180 poke v+29,dx:we=dx-4:z=13:gosub 2370:goto1290
2190 poke v+23,dy:we=dy-4:z=15:gosub 2370:goto1290
2200 goto1290
2210 : rem*********************************************************************
2220 : rem** sprites ein/aus schalten **
2230 : rem*********************************************************************
2240 for i=1 to 100
2250 geta$:if a$=""then2280
2260 ifa$=chr$(133)then 2290
2270 ifa$=chr$(137)then 2310
2280 next i: goto 1290
2290 if(peek(v+21)and1)=1thenpokev+21,peek(v+21)-1:goto2330:rem*bit 0 gesetzt?*
2300 pokev+21,peek(v+21)+1:goto2340
2310 if(peek(v+21)and2)=2thenpokev+21,peek(v+21)-2:goto2350:rem*bit 1 gesetzt?*
2320 pokev+21,peek(v+21)+2:goto2360
2330 poke211,37:poke214,20:sys58640:print"off":goto1290
2340 poke211,37:poke214,20:sys58640:print" on":goto1290
2350 poke211,37:poke214,21:sys58640:print"off":goto1290
2360 poke211,37:poke214,21:sys58640:print" on":goto1290
2370 : rem*********************************************************************
2380 : rem** cursor setzen (x-y) **
2390 : rem*********************************************************************
2400 poke211,33:poke214,z:sys58640:printleft$(dr$,9+len(str$(we)));we:return
2410 :
