Dem Klang auf der Spur - Teil 3
Nachdem im zweiten Teil dieser Reihe einige allgemeine Grundlagen aus dem Themenkomplex »Musik und Computer« dargestellt worden sind, wird in dieser Folge ausführlich der Synthesizer Chip SID (Sound Interface Device) 6581 vorgestellt.
Der SID (Sound Interface Device) ist funktionell an das klassische Konzept von Moog angelehnt. Dadurch ist seine Arbeitsweise leicht verständlich. Bild 1 zeigt das Blockschema des SID. Dieses Schema dient dazu, den Fluß der Audio-Signale zu veranschaulichen. Die Funktionsblöcke waren in ähnlicher Form bereits Bestandteile des Synthesizer-Schemas aus Teil 2. Den linken Teil des Schemas bilden drei identische, voneinander unabhängige, Funktionsgruppen.
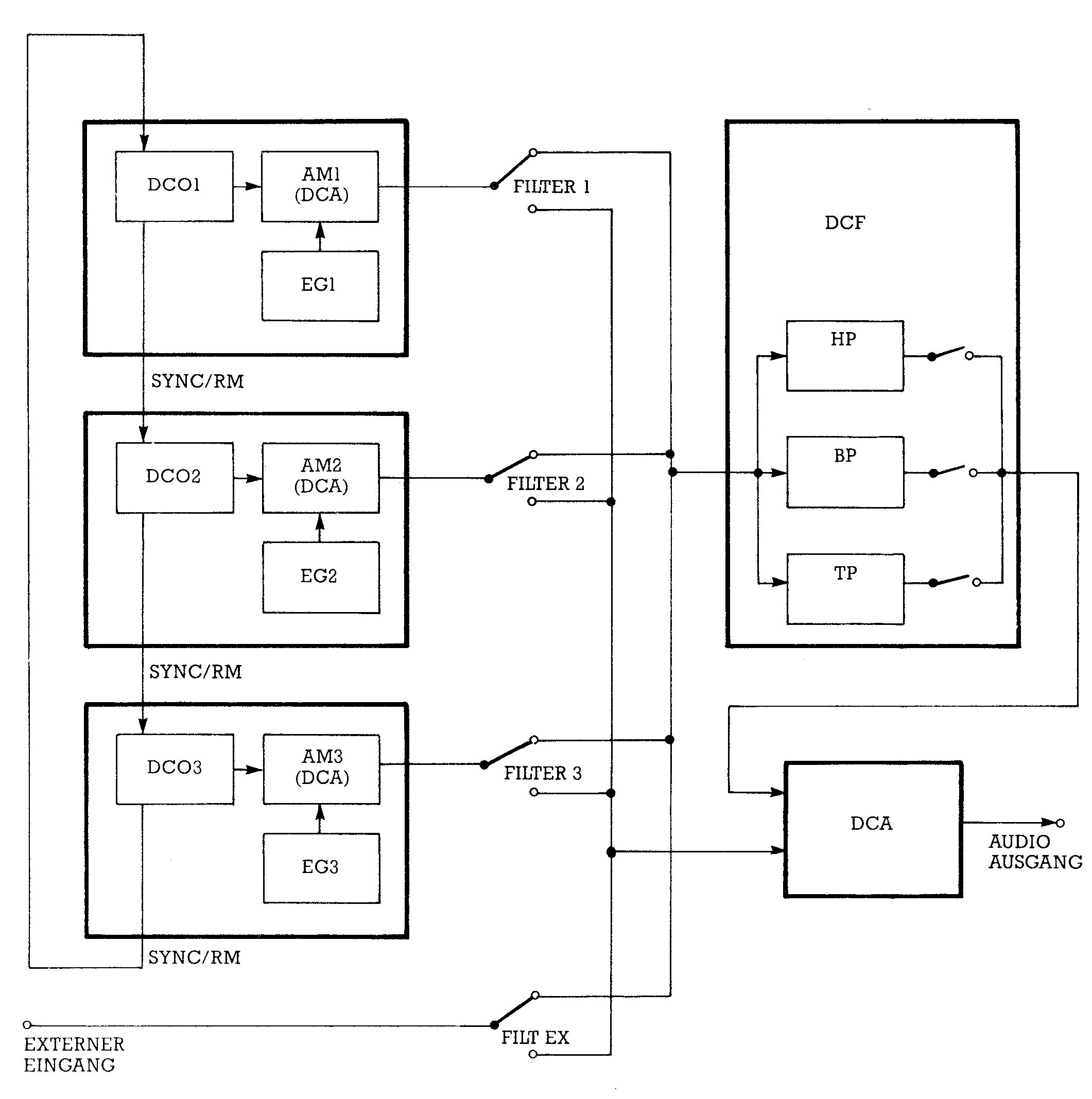
Eine solche Gruppe setzt sich aus einem DCO (Digital Controlled Oscillator), einem Amplitudenmodulator (oder auch DCA = Digital Controlled Amplifier) und einem Hüllkurvengenerator (EG = Envelope Generator) zusammen. Der DCO kann wahlweise eine von vier Kurvenformen erzeugen: Dreieck, Sägezahn, Rechteck und Rauschen. Dabei ist das Tastverhältnis der Rechteckkurve steuerbar. Unter dem Tastverhältnis versteht man das Verhältnis zwischen der Länge des Kurvenabschnitts mit hoher Spannung zur gesamten Periodenlänge. Eine symmetrische Rechteckkurve hat demnach ein Tastverhältnis von 50 Prozent. Eine Veränderung im Tastverhältnis T bewirkt eine Klangfarbenänderung. So klingt eine Rechteckkurve mit T = 50 Prozent voluminös. Bewegt man sich mit T in Richtung 0 Prozent oder 100 Prozent, so wird der Klang zunehmend obertonreicher aber dünner, da der Anteil des Grundtons abnimmt. Einen besonders lebendigen Klang erhält man durch dynamische Veränderung des Tastverhältnisses, wras zwar in der SID-Hardware nicht realisiert, aber softwaremäßig möglich ist.
Funktioneller Aufbau des SID
Der Hüllkurvengenerator beeinflußt über den Amplitudenmodulator den zeitlichen Lautstärkeverlauf der vom DCO kommenden Kurve. Die Hüllkurve wird nach dem bekannten ADSR-Schema parametrisiert.
Synchronisation und Ringmodulation
Die senkrechten Verbindungen von DCO1 zu DCO2, von DCO2 zu DCO3 und von DCO3 zurück zu DCO1 können einzeln zu- oder abgeschaltet werden. Sie dienen Spezialeffekten, die das Spektrum des SID beträchtlich erweitern. Im Normalfall, wenn diese Steuerpfade unwirksam geschaltet sind, schwingen die drei DCOs unabhängig voneinander, jeder in seiner vorprogrammierten Frequenz und Kurvenform. Im Falle der Synchronisation zwingt der synchronisierende DCO einen weiteren DCO dazu, gleichphasig zu schwingen. In Bild 2 erzeugt DCO1 eine Sägezahnschwingung von 100 Hz und synchronisiert DCO2, der ebenfalls auf Sägezahn, aber 350 Hz eingestellt ist. Nach jeweils dreieinhalb Perioden wird DCO 2 gezwungen, eine neue Periode anzufangen. DCO2 erzeugt so eine viel komplexere Kurvenform, als er es ohne Synchronisation tun würde. Variiert man nun noch die Frequenz eines der beiden DCOs, während man die des anderen konstant hält, so erzeugt DCO2 ständig andere Kurvenformen. Man erhält damit schwer zu beschreibende, aber meistens »elektronisch« (im Sinne von »unnatürlich«) klingende Muster.
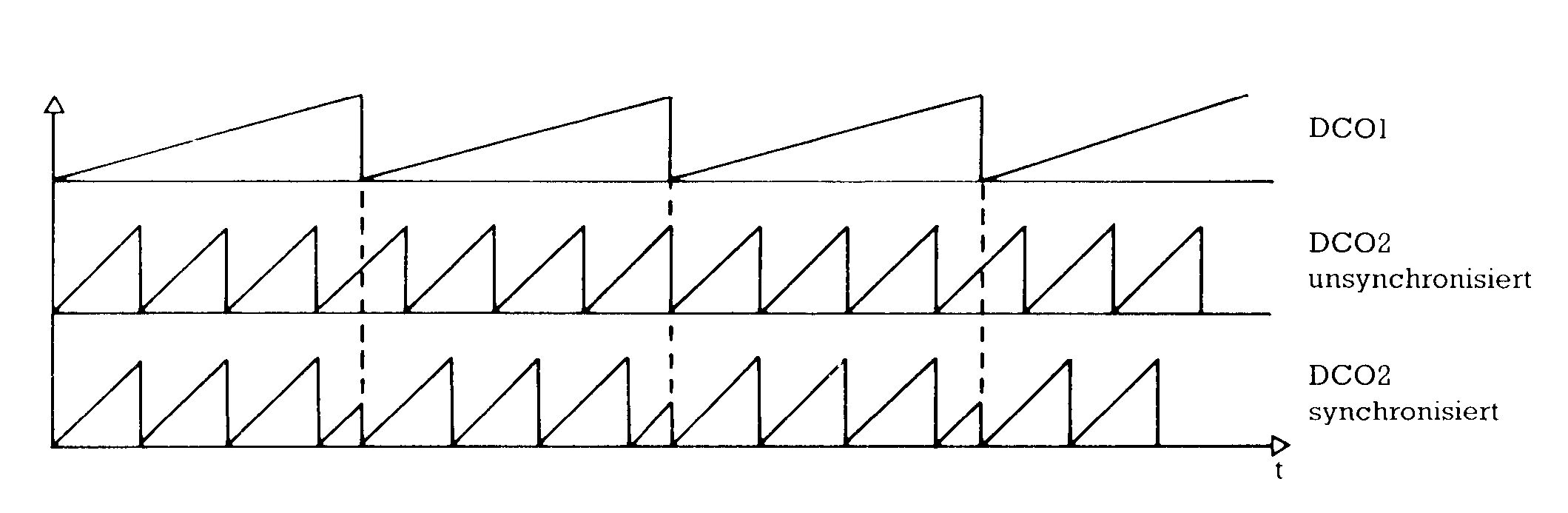
Wenn man zu jedem Zeitpunkt die Werte zweier Kurvenzüge miteinander multipliziert, so spricht man von Ringmodulation Dieser Vorgang hat eine Ähnlichkeit mit der Modulation einer Schwingung mit einer Hüllkurve, wie sie im SID auch vorkommt. Die Hüllkurve ist aber eine Funktion, die sich, verglichen mit dem Signal das sie moduliert, nur langsam verändert. Dadurch bleibt bei dieser Modulation der Klangcharakter des modulierten Signals erhalten, es ändert sich nur seine Lautstärke.
Bei der Ringmodulation dagegen ist das modulierende Signal von ähnlicher Beschaffenheit wie das modulierte Signal. Beide Signale dürfen ähnliche Frequenzen haben und als Kurvenzüge auch positive und negative Werte annehmen, wogegen eine Hüllkurve immer nur nichtnegative Werte hat. Bei der Ringmodulation geht im Allgemeinen der Klangcharakter beider beteiligten Kurven verloren; es entsteht ein ganz neuer Klang. Man macht sich das am besten anhand zweier Sinusschwingungen klar:
\[ \sin(\omega_1 t) \sin(\omega_2 t) = \frac{1}{2} \left( \cos((\omega_1 - \omega_2)t) - \cos((\omega_1 + \omega_2)t) \right) \]
Das bedeutet, daß man durch Multiplikation zweier Sinusschwingungen ein Signalgemisch erhält, das aus Schwingungen mit der Summe und der Differenz der ursprünglichen Frequenzen besteht. Die ursprünglichen Frequenzen verschwinden dabei vollkommen. Die Formel liefert auf der rechten Seite zwar Cosinus-Terme, für den Klang ist das allerdings unerheblich, da sich Sinus und Cosinus nur durch eine Phasenverschiebung unterscheiden. Unterzieht man nun andere Kurvenformen einer Ringmodulation, so muß man alle Obertöne der einen Kurve mit allen Obertönen der anderen Kurve gemäß der obigen Formel verrechnen. Dadurch entsteht ein sehr reichhaltiges neues Obertonspektrum. Die neuen Obertöne stehen dabei nicht mehr in harmonischen, das heißt ganzzahligen Verhältnissen zueinander. Aus diesem Grund eignen sich Ringmodulatorklänge auch kaum zur Wiedergabe von Melodien. Im natürlichen Umfeld findet man unharmonische Obertonverhältnisse zum Beispiel bei Glocken, Gongs und schwingenden Metallplatten. Zu deren Nachahmung eignen sich die Ringmodulatorklänge.
Beim SID steht zur Ringmodulation nur die Dreiecksschwingung zur Verfügung. Wenn DCO1 den DCO2 moduliert, ist das Ringmodulatorprodukt nur dann hörbar, wenn DCO2 auf Dreieckskurve eingestellt ist. Noch komplexere Klänge erhält man beim SID durch Einbeziehen aller drei DCOs in die Modulationskette, wobei man durch den Signalpfad DCO3 nach DCO1 den Kreis auch noch schließen kann. Die Ergebnisse werden dann allerdings schwer vorhersagbar, lassen also noch genug Räum für Experimente und Überraschungen.
Filterung
Leider hat der SID nur ein gemeinsames Filter für die drei DCO-EG-AM-Gruppen. Möchte man unterschiedliche Klangbilder zur gleichen Zeit erzeugen, so kann man nur durch die Wahl von Kurvenform und Hüllkurve differenzieren. Man hat aber immerhin die Wahl, ob man die DCO-EG-AM-Produkte überhaupt durch das Filter schickt oder am Filter vorbei direkt zum Ausgang. Diese Funktion erfüllen im Blockschema die Schalter »FILTER 1«, »FILTER 2« und »FILTER 3«. Das Filter kann als Hochpaß, als Bandpaß oder als Tiefpaß wirken, wobei die Funktionen auch parallel schaltbar sind. So erhält man zum Beispiel aus der Kombination Hochpaß und Tiefpaß eine sogenannte Bandsperre (oder »Notch-Filter«), die ein schmales Band aus dem Gesamtspektrum unterdrückt. Es sind die Parameter Eck- beziehungsweise Mittenfrequenz (für HP, BP und TP gemeinsam) sowie die Resonanz programmierbar. Ein weiteres Qualitätskriterium eines Filters ist seine Steilheit. Diese Größe beschreibt, wie schnell ein Filter in der Umgebung der Eck- beziehungsweise Mittenfrequenz vom durchlassenden in den sperrenden Zustand übergeht.
Als Faustregel gilt, daß ein Filter um so »besser« klingt, je steiler es ist. Beim Hoch- und Tiefpaß des SID beträgt die Steilheit 12 db/Oktave, beim Bandpaß 6 dB/Oktave. 12 dB/Oktave bedeuten, daß zum Beispiel im Übergangsbereich des Tiefpasses ein Signal um das Vierfache abgeschwächt wird, wenn seine Frequenz verdoppelt wird. 6 dB/Oktave bedeuten eine Abschwächung (oder Anhebung) um das Zweifache bei Frequenzverdopplung. Die Filtersteilheit ist im Allgemeinen und auch beim SID fest vorgegeben. Zur Orientierung sei noch erwähnt, daß die Filter im professionellen Synthesizer meistens eine Steilheit von 24 dB/Oktave haben.
Die gefilterten oder ungefilterten Signale im SID werden auf einen DCA geführt, wo man noch die Gesamtamplitude des Ausgangssignals programmieren kann. Über einen Analogeingang kann man auch noch ein externes Signal gefiltert oder ungefiltert zumischen. Dieses Signal könnte zum Beispiel von einem zweiten SID stammen.
Gegenüber dem im ersten Teil vorgestellten klassischen Synthesizerkonzept findet man im SID keinen LFO, mit dem man Frequenz, Amplitude oder einen Filterparameter modulieren könnte. Diese Funktion kann man aber rein softwaremäßig realisieren. Eine Hilfe dazu können DCO3 und EG3 sein. Man kann zu jedem Zeitpunkt den Amplitudenwert von DCO3 und von EG3 abfragen. Programmiert man DCO3 als LFO, das heißt auf eine sehr niedrige Frequenz, so kann man die Amplitudenwerte von DCO3 (mit geeigneter Skalierung) zur Frequenz von DCO1 oder DCO2 addieren. Tut man das in regelmäßigen Zeitabständen und mehrfach innerhalb einer Periodendauer von DCO3, so kann man damit ein Vibrato realisieren.
Auf gleiche Weise kann man auch die von EG3 gelieferte Hüllkurve zur Modulation beispielsweise des Filters heranziehen. Beide Möglichkeiten erfordern allerdings zusätzliche schnelle Programme, die sich nur in Maschinensprache realisieren lassen.
Wenn man DCO3 und/oder EG3 zu Modulationszwecken benützt, möchte man das von AM3 produzierte Signal unter Umständen nicht hören. Dazu kann man es mit dem zusätzlichen Schalter »AUS« unterdrücken.
Im letzten Teil wurde schon angesprochen, daß ein digitaler Synthesizer wie der SID nicht durch Potentiometer und durch Spannungen beeinflußt wird, sondern durch digitalisierte Parameter. Dazu besitzt der SID 29 Register mit einer Länge von 8 Bit. Davon können 25 nur beschrieben werden (ihre Inhalte steuern das Verhalten des SID) und 4 nur gelesen werden. Die 29 Register werden durch die Adreß-Decodierungs-Hardware auf dem CPU-Speicherbereich $D400 bis $D41C abgebildet (dezimal: 54272 bis 54300).
Die Steuerung des SID
Die SID-Register lassen sich so mit allen hauptspeicherbezogenen Maschinenbefehlen oder mit PEEK und POKE ansprechen. Da in einzelnen Registern oft mehrere Bits mit unterschiedlicher Bedeutung zusammengefaßt sind, erfordert ihre Programmierung ein hohes Maß an maschinennahem Denken, egal ob in Basic oder in Maschinensprache programmiert wird.
Die Tabelle 1 zeigt die Bedeutung der einzelnen Register im Detail. Der Registersatz gliedert sich in drei mal sieben Register zur Steuerung der drei DCO-EG-AM-Gruppen für die drei Stimmen, in vier Register zur Filtersteuerung und in vier Leseregister. Die sieben Register zur Steuerung einer DCO-EG-AM-Gruppe haben für alle drei Stimmen den gleichen Aufbau und die gleiche Bedeutung.
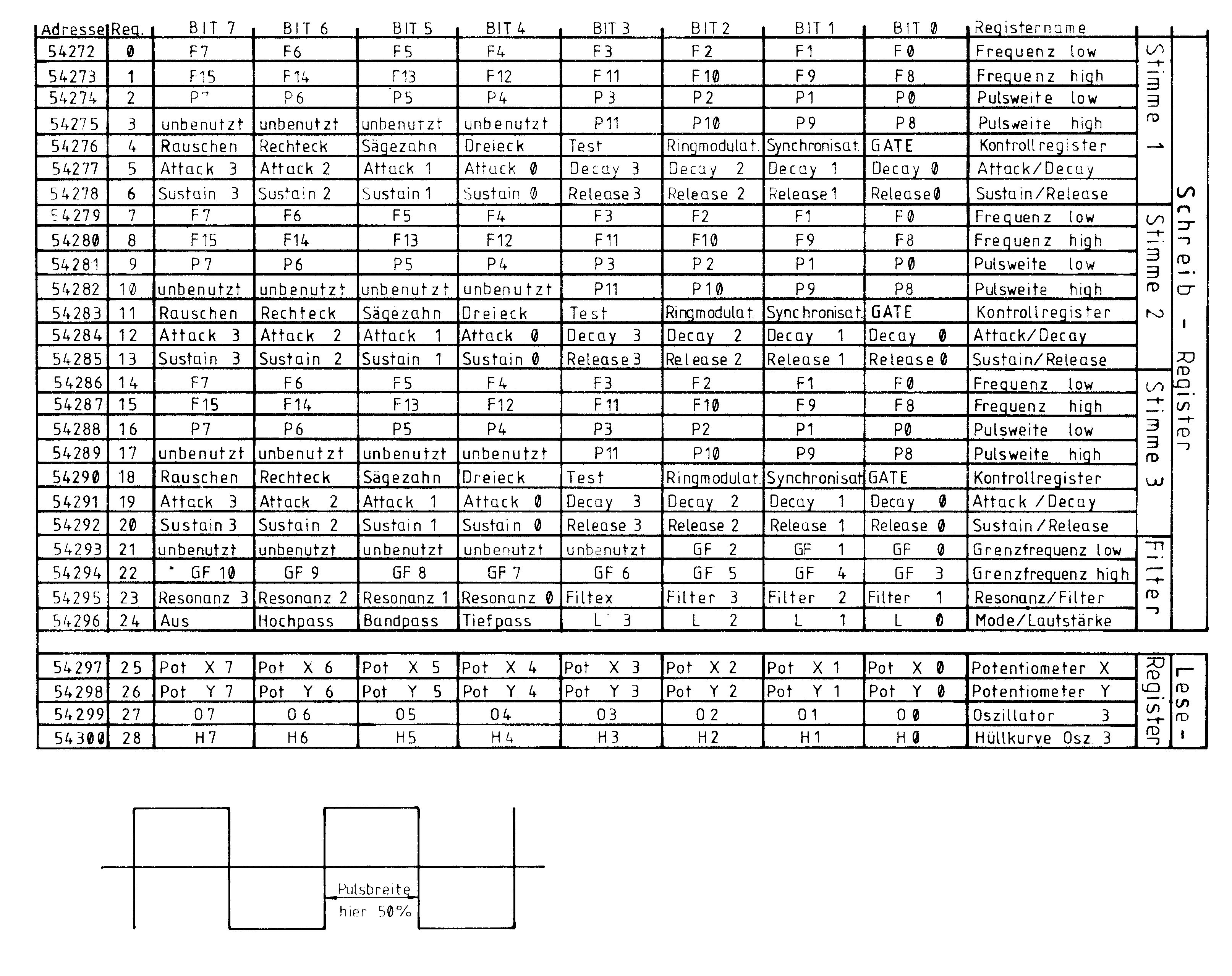
Frequenz low/high (Register 0 und 1)
Die beiden Register 0 und 1 steuern die Frequenz von DCO1 mit einer Genauigkeit von 16 Bit. Register 0 enthält das niederwertige, Register 1 das höherwertige Byte einer 16-Bit-Größe F. Zwischen der Ausgangsfrequenz f und der Zahl F besteht der Zusammenhang:
(1) f = F × T/2↑24(Hz)
Dabei ist T die Taktfrequenz der CPU, die auch am SID anliegt. Sie beträgt bei der deutschen Version des C 64 0,985248 MHz
Damit gilt:
(2) f = F × 0,0587254 (Hz) oder
(3) F = f × 17,0284
Die Gleichungen (2) und (3) zeigen, daß sich die Frequenzen der DCOs sehr fein, in Schritten zu zirka 1/17 Hz, programmieren lassen. Möchte man eine vorgegebene Frequenz f (im Beispiel FAUS) erzeugen, so errechnet man F nach (3),
10 FAUS = 440
20 F = FAUS * 17.0284
man zerlegt F in das Low- und das High-Byte,
30 F = INT(F + 0.5) :REM RUNDUNG
40 HI = INT(F/256)
50 LO = F - 256*HI
und besetzt Register 0 und 1 damit
60 SID = 54272 :REM BASISADRESSE
70 POKE SID,LO
80 POKE SID + 1,HI
Pulsweite low/high (Register 2 und 3)
Der Inhalt dieser Register steuert das Tastverhältnis der Rechteckkurve. Er ist nur dann bedeutend, wenn als Kurvenform das Rechteck gewählt wird. Die Pulsweite kann auf 12 Bit genau festgelegt werden. Register 2 enthält das Low-Byte, Register 3 das High-Byte, von dem nur die unteren 4 Bits (P8 bis P11) berücksichtigt werden. Zwischen der 12-Bit-Größe P und dem Tastverhältnis PAUS besteht der Zusammenhang:
(4) PAUS = P / 40.95 (%)
oder
(5) P = PAUS * 40.95
Die Programmierung gestaltet sich dann in der Praxis analog zu der der Frequenz:
90 PAUS = 50
100 P = PAUS * 40.95
110 P = INT(P + 0.5) :REM RUNDUNG
120 HI = INT (P/256)
130 LO = P - 256*HI
140 POKE SID + 2,LO
150 POKE SID + 3,HI
Kontrollregister (Register 4)
Jedes Bit dieses Registers hat eine eigene Bedeutung.
GATE (Bit 0)
Dieses Bit steuert den Hüllkurvengenerator EG 1. Wird es gesetzt, startet EG1 eine Ättack-Decay-Sequenz. Die Hüllkurve bleibt anschließend auf dem programmierten Sustain-Pegel, bis das GATE-Bit zurückgesetzt wird. Durch das Zurücksetzen geht die Hüllkurve in die Release-(Auskling-)Phase.
Synchronisation (Bit 1)
Wird es gesetzt, so wird DCO1 von DCO3, wie schon beschrieben, synchronisiert.
Ringmodulation (Bid 2)
Wird es gesetzt, so erzeugt DCO1 das Ringmodulatorprodukt der Dreieckskurven von DCO3 und DCO1. Diese wird allerdings nur dann hörbar, wenn als Kurvenform von DCO1 das Dreieck gewählt wird.
Test (Bit 3)
Bei gesetztem Test-Bit wird DCO1 auf Nullpegel gezwungen. Er erzeugt in diesem Zustand keine Schwingung. Man kann DCO1 damit softwaregesteuert synchronisieren, um, ähnlich wie durch die Synchronisation durch DCO3, komplexere Kurvenformen zu erhalten.
Kurvenform (Bit 4 bis 7)
Durch Setzen eines dieser 4 Bits wählt man eine der Kurvenformen Dreieck, Sägezahn, Rechteck oder Rauschen. Es muß mindestens eines dieser Bits gesetzt sein, damit überhaupt etwas hörbar wird. Eine Eigenart des SID ist es, daß sich die Kurvenformen nicht additiv verhalten. Werden mehrere der Bits 4 bis 7 zugleich gesetzt, so erzeugt der SID eine Kurvenform, deren Amplitudenwerte man durch logische AND-Verknüpfung der Amplitudenwerte der einzelnen Kurven erhält. Diese AND-Verknüpfung muß man sich bitweise auf die Amplitudenwerte darstellenden Bytes angewandt vorstellen.
Das Rauschen verdient noch eine besondere Betrachtung. Bei Rauschen kann man nicht von einer Frequenz im üblichen Sinne reden. Dennoch ist der Charakter des SID-Rauschens über die Größe F in Register 0 und 1 beeinflußbar. Rauschen wird im SID durch eine Quasi-Zufallsfolge von numerischen Werten realisiert. Die Rate, mit der der DCO diese Zufallszahlen erzeugt, ist genau die durch F programmierte Frequenz. Ein Rauschen mit »hoher Frequenz« klingt heller oder »weißer« als Rauschen mit niedriger Frequenz.
Bei der Programmierung des Kontrollregisters muß man sich vorher den Wert jedes einzelnen Bits zurechtlegen und in das Byte packen. Das Anstoßen eines Rechteckklanges beispielsweise wird durch Setzen von Bit 0 und Bit 6 erreicht. Der numerische Wert des Kontrollbytes ist dann: 2↑0 + 2↑6 = 65
also: 240 POKE SID+4,65
Ein hörbares Resultat wird aber auch erst dann erzielt, wenn vorher die Hüllkurvenparameter vernünftig gesetzt sind.
ADSR (Register 5 und 6)
Die Parameter A, D, S und R können in 16 Abstufungen entsprechend 4 Bit Auflösung programmiert werden. Die Stufung für den Sustain-Pegel ist linear. S = 0 entspricht dem Ruhepegel, S = 15 entspricht dem Maximalpegel nach Attack. Bei S = 15 besitzt die Hüllkurve keine Decay-Phase. Die Abstufungen für die Attack-, Decay- und Release-Zeiten sind vernünftigerweise nicht linear, um sehr kurze und sehr lange Zeiten gleichermaßen zu ermöglichen. Tabelle 2 enthält die realisierbaren Attack-, Decay- und Release-Zeiten.
| Wert Dez. | Hex | Attack | Decay/Release |
| 0 | 0 | 2 ms | 6 ms |
| 1 | 1 | 8 ms | 24 ms |
| 2 | 2 | 16 ms | 48 ms |
| 3 | 3 | 24 ms | 72 ms |
| 4 | 4 | 38 ms | 114 ms |
| 5 | 5 | 56 ms | 168 ms |
| 6 | 6 | 68 ms | 204 ms |
| 7 | 7 | 80 ms | 240 ms |
| 8 | 8 | 100 ms | 300 ms |
| 9 | 9 | 250 ms | 750 ms |
| 10 | A | 500 ms | 1,5s |
| 11 | B | 800 ms | 2,4 s |
| 12 | C | 1 s | 3s |
| 13 | D | 3s | 9s |
| 14 | E | 5s | 15 s |
| 15 | F | 8 s | 24 s |
Die Zeiten gelten bei einer System-Taktfrequenz von 1 MHz. Da diese Frequenz beim deutschen C 64 mit 0,985248 MHz nur gering davon abweicht, ist die Tabelle auch für diese Frequenz brauchbar.
Quelle: Commodore 64 Programmers Reference Guide
Decay und Release können direkt in die Register 5 und 6 geschrieben werden, während Attack und Sustain vorher mit 16 zu multiplizieren sind, was einer Linksverschiebung um vier binäre Stellen entspricht. Ein Beispiel:
160 A = 2 :REM 16 MS
170 D = 12 :REM 3 S
180 S = 1
190 R = 10 :REM 1.5 S
200 POKE SID + 5,A*16 + D
210 POKE SID + 6,S*16 + R
Nach vorläufigem Umgehen des Filters und Setzen der maximalen Lautstärke
220 POKE SID + 23,0 :REM FILTER AUS
230 POKE SID + 24,15 :REM LAUTSTÄRKE
führt das Setzen des GATE-Bits:
240 POKE SID + 4,65 :REM GATE AN
zu einem vernünftigen Resultat. Zum Abschalten des Klanges kann man einfach das Kontrollregister mit 0 besetzen,
270 POKE SID + 4,0
doch dann hat DCO1 keine Gelegenheit, der Release-Phase entsprechend auszuklingen, da auch das Kurvenform-Bit (Nr. 6) zurückgesetzt ist. Besser ist also, Bit 6 gesetzt zu lassen:250GETA$:IFA$ = “ " THEN 160
260 REM WARTE AUF EINE TASTE
270 POKE SID + 4,64 :REM GATE AUS
Die Basic-Zeilen zeigen natürlich keinen effizienten Programmierstil; sie sollen nur die Vorgehensweise darstellen.
Auf die Steuerung des Filters und auf die Anwendung der Leseregister wird im nächsten Teil noch ausführlich eingegangen werden. So ist die Abfrage eines analogen Gebers (zum Beispiel Paddle) erst durch den SID möglich. Die sechs kleinen Beispielprogramme demonstrieren einige Effekte, die man mit den bis hierher beschriebenen Registern realisieren kann.
(Thomas Krätzig/aa)100 si=54272 :rem basisadresse 110 : 120 rem frequenz 130 read faus :f=int(faus*17.0284+0.5) 140 hi=int(f/256) :lo=f-256*hi 150 poke si,lo :poke si+1,hi 160 : 170 rem pulsweite (tastverhaeltnis) 180 read paus :p=int(paus*40.95+0.5) 190 hi=int(p/256) :lo=p-256*hi 200 poke si+2,lo :poke si+3,hi 210 : 220 rem wellenform 230 read wf:wf=wf and 254 :rem gate aus 240 : 250 rem a d s r 260 read a:read d:poke si+5,16*a+d 270 read s:read r:poke si+6,16*s+r 280 : 290 rem filter aus, lautstaerke max 300 poke si+23,0:poke si+24,15 310 : 320 rem auf tastendruck warten 330 rem und adsr sequenz ausloesen 340 read t 350 get a$:if a$="" then 350 360 poke si+4,wf or 1 370 for i=1 to t:next 380 poke si+4,wf:goto 350 500 rem================================ 510 rem klangparameter 520 rem================================ 530 data 440 :rem frequenz (hz) 540 data 50 :rem tastverhaeltnis (%) 550 data 64 :rem kurvenform 560 data 2 :rem attack 570 data 8 :rem decay 580 data 0 :rem sustain 590 data 8 :rem release 600 data 150 :rem zeit zwischen 610 rem attack und release
10 rem================================= 20 rem programm 2 30 rem 40 rem einzeiler fuer signalton 50 rem================================= 60 s=54272:for i=0 to 6:read x:poke s+i,x:next:poke s+24,15:poke s+4,17:poke s+4,16:data 0,99,0,8,0,11,11
100 si=54272 :rem basisadresse 110 : 120 rem tastverhaeltnis = 50% 130 poke si+2,0 :poke si+3,8 140 : 150 rem adsr 160 a=0 :d=0 :poke si+5,16*a+d 170 s=15 :r=0 :poke si+6,16+s+r 180 : 190 rem filter aus und lautstaerke max. 200 poke si+23,0:poke si+24,15 210 : 220 rem flo=0, kurvenform 230 poke si,0 240 poke si+4,65 250 : 260 rem fhi auf- und abwaerts steuern 270 f0=50 :f1=100 280 for i=0.4 to 50 step .2 290 : for f=f0 to f1 step 1 300 : poke si+1,f 310 : next f 320 : for f=f1 to f0 step -1 330 : poke si+1,f 340 : next f 350 next i 360 poke si+4,64
134 rem das maschinenprogramm belegt 136 rem den bereich ($9000-$90ac) 140 rem 150 rem aufrufbedingungen 160 rem 170 rem sys par,s,pw,k,a,d,s,r 180 rem 190 rem belegt stimme s (1,2,3) mit 200 rem 210 rem pw (pulsweite 0...4095) 220 rem k (kurvenform,synchronisa- 230 rem tion,ringmodulation) 240 rem a,d,s,r (huellkurve 0..15) 250 rem 260 rem sys ein,s,f 270 rem 280 rem schaltet stimme s mit 290 rem frequenz f (0..65535) ein 300 rem 310 rem sys aus,s 320 rem 330 rem schaltet stimme s aus 340 rem================================ 360 : 370 a=36864:b=37036 380 for i=a to b 390 read x:poke i,x:s=s+x:next i 400 if s<>17579 then print"tippfehler" 410 : 420 par=a+66 :ein=a+122 :aus=a+161 430 : 440 rem datas fuer maschinenprogramm 450 : 460 data 000,000,000,000,000,032,253,174 470 data 032,158,183,224,004,048,003,076 480 data 072,178,224,000,240,249,202,188 490 data 027,144,096,000,007,014,152,072 500 data 032,253,174,032,158,183,224,016 510 data 048,003,076,072,178,104,168,138 520 data 096,032,030,144,010,010,010,010 530 data 141,000,144,032,030,144,013,000 540 data 144,096,032,005,144,138,072,152 550 data 072,032,253,174,032,235,183,142 560 data 000,144,104,168,104,170,173,000 570 data 144,157,002,144,165,021,201,022 580 data 048,003,076,072,178,153,003,212 590 data 165,020,153,002,212,032,049,144 600 data 153,005,212,032,049,144,153,006 610 data 212,096,032,005,144,138,072,152 620 data 072,032,253,174,032,138,173,032 630 data 247,183,104,168,165,020,153,000 640 data 212,165,021,153,001,212,104,170 650 data 189,002,144,009,001,153,004,212 660 data 096,032,005,144,189,002,144,041 670 data 254,153,004,212,096
100 si=54272 :rem basisadresse 110 par=36930:ein=36986:aus=37025 120 : 130 rem filter aus und lautstaerke max. 140 poke si+23,0:poke si+24,15 150 : 160 rem parametersaetze abarbeiten 170 read n 180 for i=1 to n 190 : read f,a,d,s,r,t1,t2 200 : sys par,1,0,128,a,d,s,r 210 : sys ein,1,f 220 : print"beispiel ";i;" gate an"; 230 : for j=1 to t1:next j 240 : sys aus,1 250 : print" gate aus" 260 : for j=1 to t2:next j 270 next i 500 data 6 :rem anzahl der p.saetze 510 rem================================ 520 rem parametersaetze 530 rem 540 rem f a d s r t1 t2 550 rem================================ 560 data 50000, 0, 0,15, 0, 1500, 200 570 data 25000, 0,12, 0,12, 500, 500 580 data 5000, 8, 5, 2, 5, 1500, 500 590 data 1000, 0,13, 0,12, 500,1500 600 data 750, 14, 0,15,13, 2000,2500 610 data 80, 8, 8, 8,10, 2500, 500
100 dim f(24) :rem array f. frequenzen 110 sid=54272 :rem basisadresse 120 par=36930:ein=36986:aus=37025 130 : 140 rem tonleiter-frequenzen berechnen 150 faus=110:h=2^(1/12) 160 for i=0 to 24 170 : f(i)=int(faus*17.0284+0.5) 180 : faus=faus*h 190 next i 200 : 210 rem parameter festlegen 220 pw=2048 :rem pulsweite 230 k =32 :rem kurvenform 240 a=0: d=9: s=0 :r=9 250 sys par,1,pw,k,a,d,s,r 260 sys par,2,pw,k,a,d,s,r 270 sys par,3,pw,k,a,d,s,r 280 : 290 rem filter aus und lautstaerke max. 300 poke si+23,0:poke si+24,15 310 : 320 rem zufallsmelodie 330 i=1 340 n=int(rnd(1)*25) 350 sys ein,i,f(n) 360 for j=0 to 20:next j 370 sys aus,i 380 for j=0 to 20:next j 390 i=i+1:if i=4 then i=1 400 goto 340
