Der gläserne VC 20 – Teil 5
In Folge 4 haben wir die Grundlagen für das Arbeiten mit selbstdefinierten Grafikzeichen besprochen. Diesmal werden wir sehen, welche Fähigkeiten der VIC in bezug auf Grafik sonst noch besitzt.
Beginnen wollen wir heute mit dem Bitmapping, also dem Arbeiten mit hochauflösender Grafik. Hochauflösend deshalb, weil die einzelnen Grafikpunkte sehr klein und das Gesamtbild dadurch sehr fein (eben hochauflösend) ist. Vorher aber noch eine Begriffserklärung: Bitmapping (engl. Map = Landkarte) bedeutet etwa soviel, wie den Bildschirm zu kartografieren, das heißt jede Bildschirmposition ist in hochauflösender Grafik über eine Koordinate erreichbar. Wer das Superexpander-Modul (VC 1211A) besitzt, der kann mittels einfacher Befehle wie PLOT, DRAW, CIRCLE etc. mit der Hires-(high resolution) Grafik arbeiten. Beim »nackten« VC 20 ist dies jedoch nicht so einfach möglich.
Das Bitmapping
Im Gegensatz zu anderen Computern unterstützt der VC 20 diese Art Grafik überhaupt nicht; man muß sich also eine Softwarelösung einfallen lassen.
Die einzige Möglichkeit, einzelne Grafikpunkte (auch Pixels genannt) — aus denen sich ja jedes Zeichen zusammensetzt — anzusprechen, haben wir in der letzten Folge kennengelernt. Ich spreche von der Möglichkeit, sich Zeichen selbst zu definieren.
Wollen wir also Bitmapping betreiben, so bleibt uns nichts anderes übrig, als den gesamten Bildschirm mit verschiedenen Sonderzeichen vollzuschreiben und diese dann umzudefinieren, so daß ein komplettes, neues Bild in Hires-Grafik entsteht.
Doch mit diesem Vorhaben stößt man bereits auf erste Schwierigkeiten, denn der VC 20 kann ja nur 256 verschiedene Zeichen auf einmal auf dem Bildschirm darstellen. Daher müßte man sich mit einer relativ kleinen Fläche für die hochauflösenden Pixels zufrieden geben.
Da die Anzahl der darstellbaren Zeichen (diese setzen sich — um dies noch einmal zu wiederholen — aus 8 x 8 Pixels zusammen) auf 256 beschränkt ist, muß man sich eine andere Lösung einfallen lassen. Diese ist aber — man wird es kaum glauben — bereits in den VIC eingebaut worden. Das sieht praktisch so aus: Man vergrößert die im Bildschirmspeicher abgelegten Zeichen von 8 x 8 auf 16 x 8 Pixels (bei gleicher Auflösung), wodurch sich gleichzeitig die zur Verfügung stehende Zeichenfläche erhöht. Diese Vergrößerung wird über ein bestimmtes Bit im VIC-Kontrollregister #3 eingestellt (vergleiche Folge 4, Tabelle 3). Ist Bit 0 dieser Speicherstelle auf 0, so bleibt alles wie es war, das heißt jedes Zeichen wird innerhalb einer 8 x 8-Matrix dargestellt.
Setzt man dieses Bit nun aber mit »POKE 36867, PEEK (36867) OR 1« auf 1, so sind alle Zeichen plötzlich doppelt so hoch. Ein Charakter wird nämlich innerhalb eines 16 x 8-Gitters abgebildet (Bild 1). Das ist nun alles schön und gut, einen Nachteil hat dieser Betriebszustand aber (wer es selbst ausprobiert hat wird es sicherlich schon bemerkt haben). Denn mit dem normalen Zeichensatz kommt auf dem Bildschirm keine vernünftige Zeichenfolge mehr zustande. So wird beispielsweise aus dem @ (Klammeraffe) das Zeichen
| @ |
| A |
aus dem A das Zeichen
| B |
| C |
und so fort. Drückt man nun eine Taste, so wird nicht der entsprechende Buchstabe abgebildet, sondern irgendwelche anderen Zeichen, die, wie eben beschrieben, übereinander gestapelt sind.
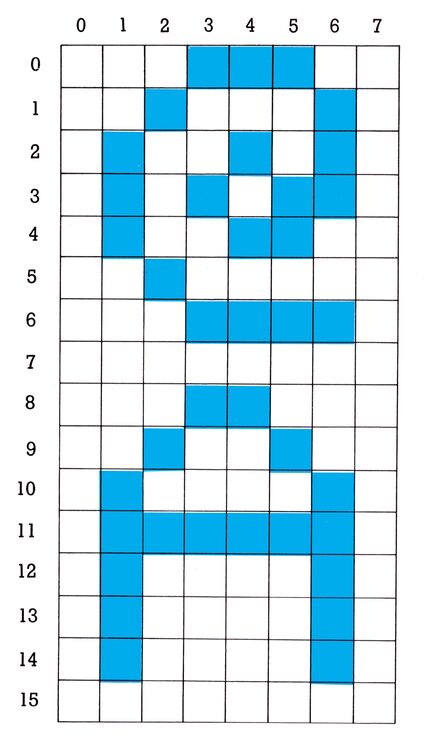
Doppelt hohe Zeichendarstellung
Die Erklärung dafür ist im Prinzip ganz einfach. Wie wir das letzte Mal gesehen haben, errechnet sich der VIC die relative Adresse eines Charakters im Zeichengenerator (relativ deshalb, weil die Adreßangaben auf eine Anfangsadresse bezogen sind), indem er den Bildschirmcode (auch hier erinnern wir uns daran, daß der Bildschirmcode die Reihenfolge der Zeichen im Charaktergenerator ist) jeweils mit 8 multipliziert.
Durch die Umschaltung auf 16-zeilige Zeichen liest der VIC für einen Charakter 16 Zeilen aus dem ROM. Daher werden — da das Zeichengenerator-ROM auf achtzeilige Zeichen ausgelegt ist — eben die Informationen von ursprünglich zwei Zeichen in einem dargestellt. Folglich multipliziert der VIC bei der Adreßermittlung den Bildschirmcode nicht mehr mit 8, sondern mit 16.
Auf diese Weise erklärt sich auch der Zahlensalat in diesem Betriebsmodus. Diese Darstellungsart hat jedoch den erheblichen Vorteil, daß jetzt mehr Zeichen als normalerweise abgebildet werden können. Es sind nämlich bereits in 128 Zeichen die Informationen von ursprünglich 256 Zeichen enthalten. Bei dem 129. Zeichen (RVS ON und @) beginnt daher schon der zweite Zeichensatz des VC. Somit lassen sich diese zwei erstmalig gemeinsam auf dem Bildschirm ausdrucken. Statt bisher 256 »normaler« Zeichen läßt sich nun die gleiche Menge in doppelter Höhe (das entspricht also 512 regulären Zeichen) abbilden. Damit sind wir jetzt in der Lage, den gesamten Bildschirm füllen zu können. Darauf gehen wir aber später noch ausführlicher ein.
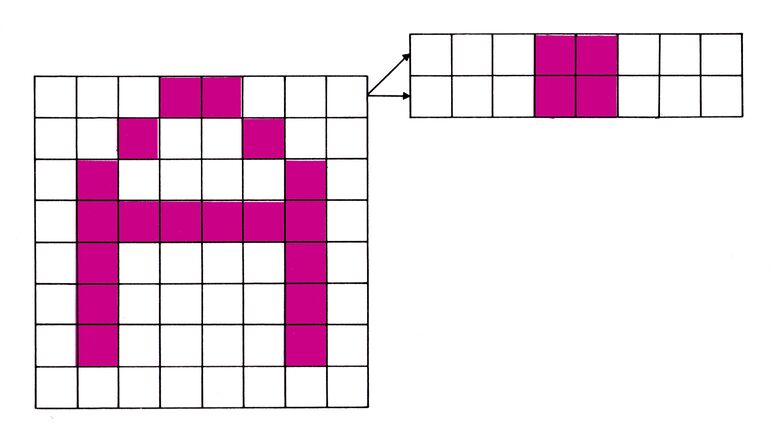
Das Naheliegendste wäre es ja nun, den Zeichengenerator ins RAM zu verlegen und dabei die Zeichen so umzubauen, daß man sie wieder richtig lesen kann. Dazu muß beim Kopieren jede Zeile verdoppelt werden; sonst bleibt ja alles beim Alten.
Das Programm in Listing 1 enthält zwei Zähler. Der eine zählt die ROM-, der andere die RAM-Speicherplätze, wobei letzterer genau doppelt so schnell läuft, denn eine ROM-Zeile soll ja zweimal hintereinander ins RAM geschrieben werden (dieses »Strecken« eines Zeichens ist in Bild 2 zu sehen). Da diese Schriftart natürlich besonders auffällig ist, eignet sie sich beispielsweise für Schaufensterwerbung oder ähnliches.
100 rem ******************************* 110 rem *** *** 120 rem *** doppelt hohe zeichen- *** 130 rem *** darstellung. *** 140 rem *** *** 150 rem *** a c h t u n g ! ! *** 160 rem *** bei 8 kbyte erweiter. *** 170 rem *** vor dem laden *** 180 rem *** >> poke 44,32 << *** 190 rem *** eingeben !!!! *** 200 rem ******************************* 210 poke55,0:poke56,24:clr 220 rem *** zeile 210 entfaellt bei 230 rem *** der 8 kbyte erweiterung. 240 aw=6144:ew=7147:g=14 250 rem *** bei 8 kbyte erweiterung 260 rem *** zeile 230 folgendermassen 270 rem *** aendern : 280 rem *** aw=5120:ew=8192:g=13 290 z1=32768 300 forz2=awtoewstep2 310 we=peek(z1) 320 pokez2,we:pokez2+1,we 330 z1=z1+1:next 340 poke36869,peek(36869)org 350 poke36865,21 360 poke36867,33
100 REM ******************************* 110 REM *** *** 120 REM *** DOPPELT HOHE ZEICHEN- *** 130 REM *** DARSTELLUNG. *** 140 REM *** *** 150 REM *** A C H T U N G ! ! *** 160 REM *** BEI 8 KBYTE ERWEITER. *** 170 REM *** VOR DEM LADEN *** 180 REM *** >> POKE 44,32 << *** 190 REM *** EINGEBEN !!!! *** 200 REM ******************************* 210 POKE 55,0:POKE 56,24:CLR 220 REM *** ZEILE 210 ENTFAELLT BEI 230 REM *** DER 8 KBYTE ERWEITERUNG. 240 AW=6144:EW=7147:G=14 250 REM *** BEI 8 KBYTE ERWEITERUNG 260 REM *** ZEILE 230 FOLGENDERMASSEN 270 REM *** AENDERN : 280 REM *** AW=5120:EW=8192:G=13 290 Z1=32768 300 FOR Z2=AW TOEWSTEP 2 310 WE=PEEK (Z1) 320 POKE Z2,WE:POKE Z2+1,WE 330 Z1=Z1+1:NEXT 340 POKE 36869,PEEK (36869)OR G 350 POKE 36865,21 360 POKE 36867,33
Wir wollen uns aber nun wieder unserem eigentlichen Thema — dem Bitmapping — zuwenden. Wie so oft stellt sich auch hier wieder die Frage nach dem Speicherplatz. Denn egal mit welcher Speicherausbauversion man gerade arbeitet, immer kommt es zu Kollisionen zwischen dem Zeichen- und dem Bildschirmspeicher. Daher müssen wir hier die Anzahl der verfügbaren Zeichen dementsprechend reduzieren. Wenn wir möglichst den ganzen Bildschirm füllen wollen, so muß es immer zu einem Kompromiß zwischen Bildschirmgröße und Speicherplatz kommen — logisch, denn je größer die verfügbare Hires-Fläche sein soll, um so mehr Speicherplatz benötigt man für die Sonderzeichen, über die das Bitmapping abgewickelt wird.
Ich glaube, mit 189 je 16 x 8 Bit-Zeichen einen solchen Kompromiß gefunden zu haben. Anhand von Listing 2, das in mehrere Teile gegliedert ist, möchte ich das Verfahren beim Bitmapping erklären. Programmteil 2 beschreibt den Bildschirm mit den veranschlagten 189 Zeichen. Vorher wird der Rahmen noch entsprechend der etwas »krummen« Zeichenzahl angepaßt. Denn da eben nicht der gesamte Bildschirm genutzt werden kann, wird der leere Rest einfach abgeschnitten, was durch Verkleinerung der Bildschirmfläche geschieht. Wenn man die Zeilen 240 — 260 aus dem Programm herausläßt, sieht man das ganz deutlich. In Teil 3 des Listings wird dann schließlich der gesamte Zeichengenerator von Adresse 5120 bis 8192 gelöscht, damit der Bildschirm auch wirklich restlos leer ist.
Damit sind alle Vorbereitungen getroffen, die wir vor dem eigentlichen Plotten durchführen müssen. Nun geht es darum, die eingegebenen Koordinaten aus den Variablen X und Y so umzuwandeln, daß die entsprechende Zeichenzeile im Charaktergenerator verändert werden kann. Als erstes verschaffen wir uns einen Überblick, wie die Zeichen auf dem Bildschirm angeordnet sind (Bild 3).
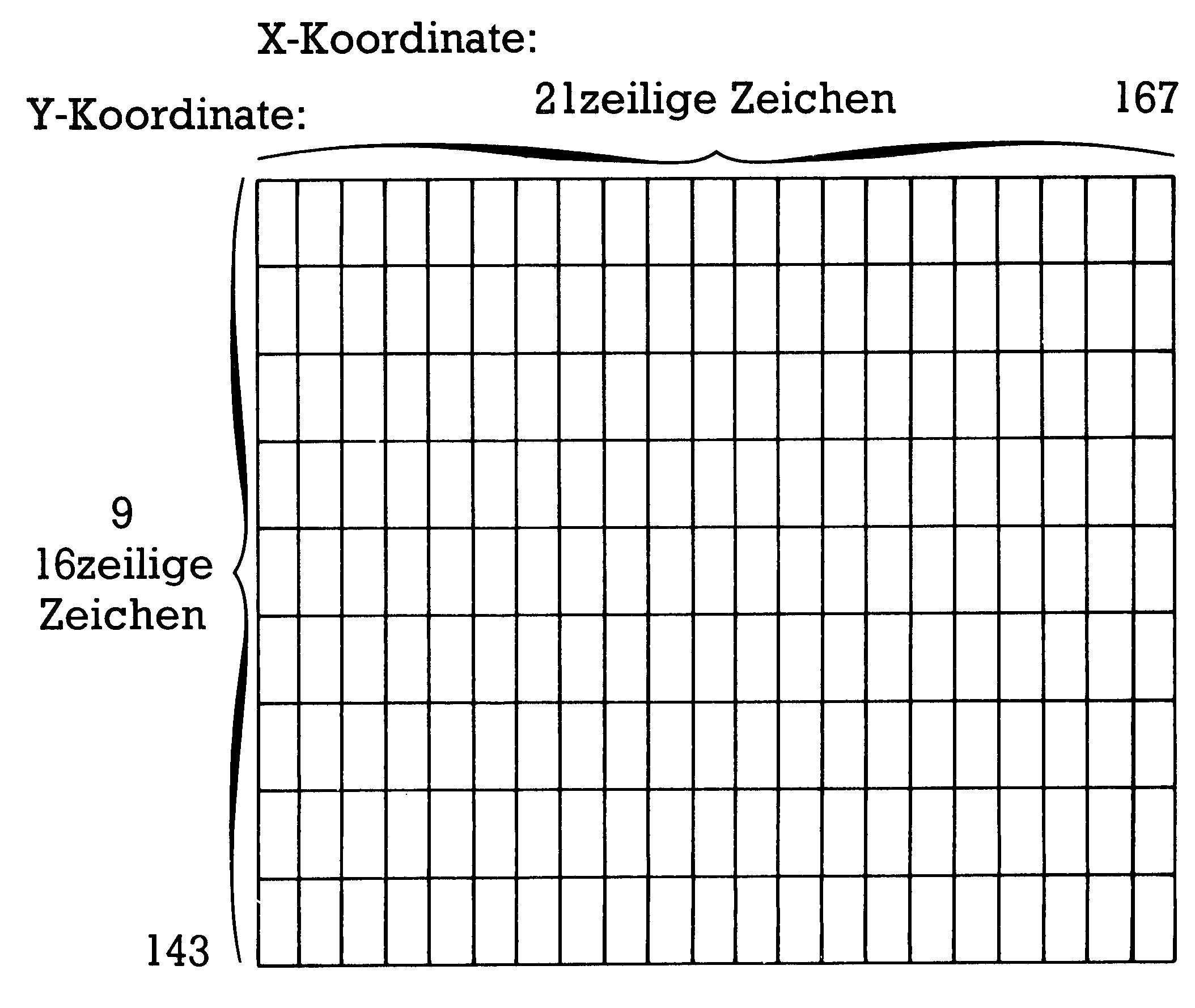
Durch die Verkleinerung der Fläche ergeben sich bei 189 verteilten Zeichen 21 Spalten und 9 Zeilen. Eine Spalte ist immer noch 8 Bit breit, denn sie rührt ja von der Zeichenbreite her. Daher ergibt sich durch Multiplikation eine Gesamtbreite von 168 Pixels. Analog verhält es sich mit der Zeilenzahl: 9 Zeilen à 16 Zeichenzeilen ergibt 144 als maximale Y-Koordinate. Übrigens hat das Koordinatensystem seinen Ursprung (X = 0/ Y=0) nicht — wie in der Mathematik — links unten, sondern links oben.
Die Koordinaten müssen aus programmtechnischen Gründen in zwei Teile aufgespalten werden; nämlich in den sogenannten Grob- (oder auch Zeichen-) anteil und in den Feinanteil (auch Pixelposition genannt).
Die Koordinatenumrechnung
Der Grobanteil ist nötig, damit zunächst einmal die Anfangsadresse eines Zeichens im Zeichengenerator festgestellt werden kann. Mit Hilfe des Feinanteils adressiert man dann die benötigte Zeichenzeile und in dieser dann die Pixelposition (aber dazu später mehr).
Anhand eines konkreten Beispiels wollen wir den zur Berechnung nötigen Algorithmus entwickeln: Der Punkt mit den Koordinaten X = 43 und Y= 106 soll auf dem Bildschirm gesetzt werden.
Nun wird als erstes festgestellt, in welchem Zeichen eine Änderung vorgenommen werden muß. Zu diesem Zweck wird die Koordinate in die besagten Grobanteile aufgespalten, was durch einfache Division geschieht. Die Spaltenkoordinate wird durch 8 (Zeichenbreite), der Zeilenanteil wird durch 16 (Zeilenhöhe) dividiert:
| X: | 43 | ÷ | 8 | = | 5 | Rest | 3 |
| Y: | 106 | ÷ | 16 | = | 6 | Rest | 10 |
Das Ergebnis ist jeweils der Grobanteil, der Rest ist dann automatisch die Pixelposition ( = Feinanteil). Der erste Teil dieser Rechnung wird in Listing 2 in den Zeilen 640 und 650 durchgeführt.
Danach wird die relative Position eines Zeichens im Charaktergenerator ermittelt. Die dafür nötigen »Formeln« haben wir ja bereits das letzte Mal besprochen:
Position = ZY x Zeichen pro Zeile + ZX
= 6 x 21 ÷ 5 = 131.
Das betreffende Zeichen hat also den Bildschirmcode 131. Da ein Charakter (nach der Umschaltung auf eine 16 x 8 Matrix) den Platzbedarf von 16 Byte hat, kann man auch ganz leicht die Anfangsadresse der ersten Zeichenzeile errechnen:
ADRESSE = Position x Platzbedarf + Basisadresse = 131 x 16 + 5120 = 7216
Dann ermitteln wir als nächstes über den Pixelanteil der Y-Koordinate die benötigte Zeichenzeile. In unserem Beispiel muß zur Zeichenadresse der Wert von PY — also 10 — dazuaddiert werden. Damit haben wir die endgültige Adresse der angewählten Zeichenzeile berechnet. Dies klingt alles viel komplizierter, als es in Wirklichkeit ist, denn alle drei Schritte können zu einem (Zeile 690) zusammengefaßt werden.
Damit sind wir schon fast am Ziel (das kann man hier sogar wörtlich nehmen) angelangt. Als letztes muß das durch die Pixel-X-Koordinate vorgegebene Bit in der Zeichenzeile gesetzt werden. Dies wird durch eine ODER-Verknüpfung des Wertes mit der Zeichenzeile erreicht.
Vorher ist aber noch eine letzte Hürde zu überwinden, die Koordinate ist nämlich nicht Byte-identisch. Was bedeutet das? Nun, unser Bildschirm entspricht beim Bitmapping ja auch einem Koordinatensystem. Denn über die horizontale (X-) und die vertikale (Y-) Koordinate läßt sich jeder beliebige Pixelpunkt durch ein Zahlenpaar (eben durch den X- und Y-Wert) eindeutig adressieren. Dabei hat der Punkt links oben die Koordinaten (0/0), der rechts unten die Koordinaten (167/143).
Für die X-Achse bedeutet dies, daß der Wert nach rechts ansteigt. Für die Fein-X-Koordinate gilt natürlich das Gleiche; sie kann von links nach rechts folgende Positionen annehmen: 0,1,2,3,4,5,6,7.
Hier liegt nun der springende Punkt. Position 0 entspricht nämlich Bit 7 in der Zeichenzeile, Position 1 Bit 6, die Position 2 Bit 5 und so fort. Diese Bits laufen also genau in entgegengesetzter Richtung. Folglich muß die Pixel-X-Koordinate dementsprechend »umgepolt« werden. Dies wird ganz einfach dadurch erreicht, indem man diesen Wert von der 7 subtrahiert:
Bitformat = 7 — (Pixel-X-Koordinate)
In unserem Beispiel ergibt sich: Bitposition= 7 — 3 = 4
Bit 4 soll nun in der Zeichenzeile gesetzt werden. Dies erreichen wir — wie bereits erwähnt — durch die ODER-Verknüpfung des Wertes mit dem Zeichenbyte. Wer den letzten Teil aufmerksam verfolgt hat, dem wird dies nicht schwerfallen. Da Bit 4 die Wertigkeit 16 (= 24) hat, wird die Zeichenzeile eben mit 16 ODER-verknüpft.
Wenn man alle drei Schritte zusammenfaßt, ergibt sich folgende Zeile:
POKE AD, PEEK (AD) OR 2 ↑ (7-PX).
Damit ist der entsprechende Pixelpunkt gesetzt. Mit diesem letzten Teilstück haben wir nun endlich den kompletten Routinenteil beieinander, um ihn als Unterprogramm in Teil 4 von Listing 2 zu verwenden. Natürlich können mit Hilfe dieser Methode auch Punkte gelöscht oder abgefragt werden. Das Löschen wird mit Hilfe der AND-Operation bewerkstelligt. Das zu löschende Bit muß im Operanden auf Null, alle anderen, die unberührt bleiben sollen, auf eins gesetzt werden. Folgende Zeile löscht den adressierten Pixelpunkt:
POKE AD, PEEK (AD) AND 255-2↑ (7-PX).
Die Abfrage von Punkten wird ebenfalls über die AND-Operation abgewickelt. Das gewünschte Bit wird im Operanden gesetzt und danach mit der Speicherstelle UND-verknüpft. Ist das adressierte Pixel gesetzt, so ist die IF-THEN-Bedingung erfüllt, ansonsten nicht:
IF 2↑ (7-PX) = (PEEK(AD) AND 2↑ (7-PX)) THEN…
Natürlich sollte man anstelle des Ausdrucks 2↑ (7-PX) eine Variable definieren, damit das Programm kürzer und schneller wird.
Zeichnen auf dem Bildschirm — der Joypainter
Soweit also die Erklärung des Bitmapping beim VC 20. Um einmal zu zeigen, was man mit diesen Erkenntnissen anfangen kann, habe ich ein Joypainter-Programm in Maschinensprache entwickelt. Der Basic-Lader (Listing 3 und 4) transferiert das Programm aus den DATA-Zeilen automatisch in die Speicherbereiche ab $2000 und nur dort ist es lauffähig (Der Speicher muß also um mindestens 8 KByte erweitert sein). Beide Listings müssen nacheinander geladen und gestartet werden. Zunächst zur Bedienung der Routine, die mit »SYS 9682« gestartet wird.
Der Joystickpainter arbeitet — wie der Name bereits sagt — mit dem Joystick. Der kleine »Zeichencursor« kann mit dem Steuerknüppel in alle vier Himmelsrichtungen und in alle Diagonalen bewegt werden.
Es ist aber auch möglich, den Cursor über die Tasten E, S, D und X zu bewegen (ganz nach Belieben). Auch die Cursortasten können für die Steuerung herangezogen werden, über die Tastatur hat man allerdings nur vier Bewegungsrichtungen für den Zeichencursor zur Verfügung. Die Tasten verwendet man sinnvollerweise dann, wenn es darum geht, besonders exakt zu zeichnen. Aus diesem Grund kann man auch die Bewegungsgeschwindigkeit über die Funktionstasten F5 und F7 auf schnell beziehungsweise langsam stellen.
Gezeichnet wird mit den Funktionstasten F1 und F3. Die obere setzt einen Punkt (und rückt den Cursor um eins nach rechts), die andere löscht einen Punkt (diese Tasten haben eine Wiederholungsfunktion). Auch der Feuerknopf kann zum Zeichnen verwendet werden. Ein kurzer Druck bewirkt das Setzen, ein langer das Löschen eines Pixels. Über die CTRL-Taste können darüber hinaus noch andere Funktionen wie Dauerzeichnen oder Dauerlöschen angewählt werden. Tabelle 1 zeigt den kompletten Befehlsvorrat.
| Taste | Funktion |
| F1 | Punkt setzen |
| F3 | Punkt löschen |
| F5 | Cursor auf schnelle Bewegung umschalten |
| F7 | Cursor auf langsame Bewegung umschalten |
| E | Steuertasten für den Zeichencursor |
| S | |
| D | |
| X | |
| CTRL C | Bildschirm löschen |
| CTRL F | Farbe des Bildschirmes mit den Tasten + und — ändern. Mit RETURN beendet man die Farbeinstellung |
| CTRL L | LOAD von Band oder Floppy |
| CTRL S | SAVE von Band oder Floppy |
| CTRL F1 | Zeichenmodus: Der Joystick (oder die Tasten) werden zu einem Zeichenstift, das heißt, bei jeder Bewegung wird ein Punkt gesetzt. |
| CTRL F3 | Radiermodus: Joypainter wird auf Dauerlöschen umgeschaltet. |
| SHIFT | »hebt« den Zeichenstift, beziehungsweise den Radiergummi. Solange man diese Taste drückt, kann man den Cursor bewegen, ohne daß das Bild verändert wird. |
| RUN/STOP | Hebt den Zeichen- beziehungsweise Radiermodus ganz auf |
Natürlich fehlen diesem Programm — da es nicht allzu lang ist — einige Funktionen, die es noch komfortabler machen würden, wie beispielsweise die Verschiebung eines Zeichenblocks auf dem Bildschirm. Solch ein Programm würde aber samt Erklärung den Rahmen dieses Kurses sprengen.
Diejenigen, die einige Routinen wie das Bitmapping-Unterprogramm oder ähnliches in ihren eigenen Programmen verwenden möchten, finden in Tabelle 2 eine Auflistung der wichtigsten Programmteile.
| Anfangsadresse | Funktion |
| $2000 | Cursortasten abfragen |
| $2047 | Joystickabfrage |
| $2084 | Startbild (64’er....) |
| $21B2 | Grafik (Bitmapping) einschalten |
| $21DC | Grafik löschen |
| $21F5 | Koordinaten-Umrechnung |
| $225F | Punkt setzen |
| $226B | Punkt löschen |
| $2279 | Punkt abfragen |
| $22D9 | Feuerknopf Verarbeitung (kurzer Druck, langer Druck) |
| $233D | Joypaintroutine |
| $2410 | Kontrolltastenabfrage und -verarbeitung |
| $25D2 | Startadresse |
Das Unterprogramm zur Joystickabfrage wird übrigens in der nächsten Folge ausführlicher besprochen. Einen bedeutenden Nachteil hat die Hires-Grafik aber, sie ist nämlich ziemlich farblos. Warum ist dies so?
Da sich diese Grafikart aus den 8 x 8- (oder 16 x 8-) Basiszeichen zusammensetzt, kann man — wie es auch bei »normalen« Buchstaben und Grafikzeichen üblich ist — jeder Videospeicherposition über das Farb-RAM jeweils nur eine Farbe (von 0 bis 7) zuweisen.
Die Darstellung von verschiedenen Farben innerhalb eines Zeichens ist also nicht möglich. Für manche Zwecke benötigt man aber nun gerade mehrere Farben innerhalb einer Zeichenmatrix. In diesem Fall wird dann ganz einfach auf den Multicolormodus — den wir im folgenden genauer besprechen werden — umgeschaltet.
Buntes Alleriei: Multicolor
Ist innerhalb eines 8 x 8 Zeichengitters irgendwo ein Bit mit dem Wert 1, so wird die entsprechende Bildschirmzelle mit dem Farbwert, der in der zugehörigen Farbspeicherstelle steht, ausgefüllt. Befindet sich in dieser Pixelzelle der Binärwert 0, so wird diese in der Hintergrundfarbe auf dem Bildschirm abgebildet (sie ist also nicht zu sehen).
In einem normalen hochauflösenden Zeichen können also zwei verschiedene Farben dargestellt werden:
- Bit auf 0: Pixeldarstellung in Hintergrundfarbe
- Bit auf 1: Pixeldarstellung in Vordergrundfarbe (Farb-RAM)
Wie Sie sehen, kann man die zwei Zustände auch als Farbcodes interpretieren. Ebenso verhält es sich im Multicolormodus: Hier werden nun zwei Bit in einer Zeichenzeile zusammengefaßt, die ebenfalls einen solchen Farbcode (allerdings für vier Farben) bilden. Ein Pixel ist in diesem Fall dann aber auch doppelt so breit wie normal, wodurch sich auch die Auflösung um die Hälfte reduziert. Bild 4 verdeutlicht den Unterschied zwischen diesen beiden Grafikarten. Diese vier möglichen Farbcodes sind auch hierbei wiederum nur die Zeiger auf Speicherstellen, in denen die eigentlichen Farbinformationen enthalten sind. Hier die möglichen Kombinationen:
| 00 | : Hintergrundfarbe |
| 01 | : Rahmenfarbe |
| 10 | : Zeichenfarbe |
| 11 | : Hilfsfarbe |
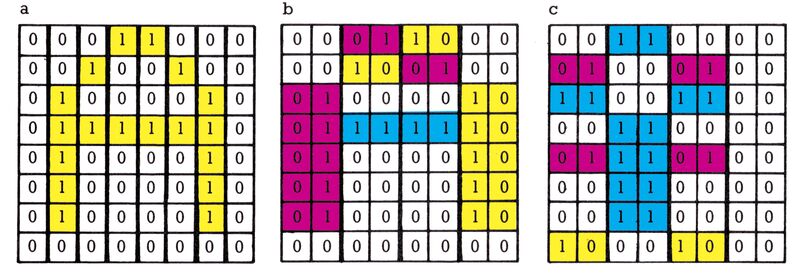
Die Werte 00 und 01, also Hintergrund- und Rahmenfarbe zeigen auf das VIC-Register # 15 (36879), in dem ja die Informationen über Rahmen- und Hintergrundfarbe abgelegt sind. Diese Farben sind also für alle Multicolorzeichen einheitlich vorgewählt. Auch der Code 11 — die Hilfsfarbe — wird einheitlich vorgewählt. Dieser Farbwert wird allerdings in einem Register gespeichert, das eigentlich mit Grafik überhaupt nichts zu tun hat, nämlich dem VIC-Register # 14 (36878), mit dem ja auch die Lautstärke festgelegt wird. Die Bits 0 bis 3 enthalten also den Lautstärkewert, die oberen vier Bit die Hilfsfarbe. Diese muß demnach speziell für Multicolor eingestellt werden, denn normalerweise ist diese Speicherstelle auf Null gesetzt (damit die Lautstärke ebenfalls null ist).
Schließlich ist noch Farbcode 10 zu erwähnen. Dieser wird für jedes Zeichen einzeln in der entsprechenden Farbspeicherstelle — wie wir es ja von den Hires-Zeichen her kennen — bestimmt. Die Bits 0 bis 2 speichern die gewünschte Farbe, Bit 3 hat eine besondere Funktion: Über dieses Bit wird — und das ist neu — der Grafikmodus ausgewählt. Ist es auf 0 (was ja der Normalfall ist), so stellt der Computer den in der dazugehörigen Videospeicherposition abgelegten Charakter im Zweifarbmodus (also in Hires-Grafik) dar. Setzt man das Bit 3 nun aber auf 1, so wird der Vierfarbmodus für dieses Zeichen eingeschaltet.
Folglich kann also die Darstellungsart für jedes Zeichen im Farb-RAM selektiert werden. Daher kann also sowohl der eine, als auch der andere Grafiktyp gleichzeitig auf dem Bildschirm abgebildet werden.
Probieren Sie es gleich einmal aus: die 1, also das Zeichen A, wird in die Bildschirmspeicherstelle 7680 (4096) gePOKEt. Danach ist in der entsprechenden Farbspeicherstelle der Colorwert mit POKE 38400,6 (beziehungsweise 37888,6) zu vermerken. In der linken oberen Ecke steht also nun ein blaues »A«. Als nächstes wird Bit 3 im Farb-RAM für diese Zeichen gesetzt:
POKE 38400, PEEK (38400) OR 8.
Nun verschwimmen die Konturen des Charakters und ein farbiges Gebilde erscheint, das nur noch entfernt an den Buchstaben A erinnert. Nun, wie Sie schon bei den doppelt hohen Zeichen gesehen haben, ist das Zeichengenerator-ROM für eine bestimmte Betriebsart konzipiert. Natürlich werden die Zeichen deshalb in hochauflösender Grafik dargestellt, damit sie besser unterscheidbar sind. Da der Zeichengenerator wiederum nur für Hires-Zeichen konzipiert wurde, kann man in Multicolor nicht viel mit ihnen anfangen.
Wegen ihrer geringen Auflösung eignet sich diese Betriebsart sowieso nur für Spielfiguren oder ähnliche Zeichen. Dazu muß der Zeichengenerator wieder ins RAM verlegt werden, was ja durch eine Änderung im Register #5 geschieht. Dann können die Zeichen wie in Bild 4 programmiert werden. In Listing 5 ist eine solche Routine zu finden. Sie erzeugt ein kleines Multicolor-Männchen (der Klammeraffe @ wird entsprechend umdefiniert).
Soweit unser etwas ausgedehnter Exkurs in die Welt der VC 20-Grafik, mit dem ich diese Folge beschließen möchte. In der nächsten Folge unseres Kurses möchte ich noch einmal auf das Betriebssystem und dessen Routinen eingehen, denn auch hier tut sich dem Programmierer ein weites Betätigungsfeld auf.
(Christoph Sauer/ev)100 rem ******************************* 110 rem *** vc 20 bitmappingroutine *** 120 rem *** fuer speicher >8 kbyte *** 130 rem *** *** 140 rem *** a c h t u n g ! *** 150 rem *** vor dem laden *** 160 rem *** >> poke 44,32 << *** 170 rem *** eingeben !!!! *** 180 rem ******************************* 190 rem 200 rem 210 rem ---------- teil 1 ------------- 220 rem 230 rem *** bildschirm einrichten 240 poke36864,13 : rem linker rand 250 poke36865,44 : rem oberer rand 260 poke36866,21 : rem 21 spalten 270 poke36867,19 : rem 18 zeilen (16*8) 280 poke36869,205 : rem zeichen ab 5120 290 rem 300 rem ---------- teil 2 ------------- 310 rem 320 rem *** 189 zeichen in den bild- 330 rem *** schirmspeicher poken. 340 fort=0to188:poke4096+t,t 350 poke37888+t,6:next 360 rem 370 rem ---------- teil 3 ------------- 380 rem 390 rem *** hiresscreen loeschen 400 fort=0to3024:poke5120+t,0:next 410 rem 420 rem ---------- teil 4 ------------- 430 rem 440 rem 450 rem *** hier wurde als demon- 460 rem *** strationsbeispiel eine 470 rem *** sin-funktion eingesetzt. 480 forx=0to167 490 y=(sin(x*2*~/167)+1)*71.7 500 gosub 640 510 next 520 goto520 530 rem 540 rem ---------- teil 5 ------------- 550 rem 560 rem *** bitmappingroutine 570 rem *** ================= 580 rem *** die hochaufloesenden pixels 590 rem *** koennen ueber koordinaten 600 rem *** angesprochen werden. 610 rem *** die x-koordinate muss <168, 620 rem *** y muss <144 sein. 630 rem 640 zx=int(x/8) : px=x-zx*8 650 zy=int(y/16): py=y-zy*16 660 rem *** die koordinaten werden in 670 rem *** einen zeichen- und einen 680 rem *** pixelanteil aufgespalten. 690 ad=5120 +zx*16 +zy*336 +py 700 rem *** ad ist die zeilenadresse 710 rem *** eines chatnrakters im zei- 720 rem *** chengeneraror ram. 730 poke ad,peek (ad) or (2^ (7-px)) 740 rem *** in dieser zeile wird das 750 rem *** gewuenschte pixel gesetzt. 760 return
100 REM ******************************* 110 REM *** VC 20 BITMAPPINGROUTINE *** 120 REM *** FUER SPEICHER >8 KBYTE *** 130 REM *** *** 140 REM *** A C H T U N G ! *** 150 REM *** VOR DEM LADEN *** 160 REM *** >> POKE 44,32 << *** 170 REM *** EINGEBEN !!!! *** 180 REM ******************************* 190 REM 200 REM 210 REM ---------- TEIL 1 ------------- 220 REM 230 REM *** BILDSCHIRM EINRICHTEN 240 POKE 36864,13 : REM LINKER RAND 250 POKE 36865,44 : REM OBERER RAND 260 POKE 36866,21 : REM 21 SPALTEN 270 POKE 36867,19 : REM 18 ZEILEN (16*8) 280 POKE 36869,205 : REM ZEICHEN AB 5120 290 REM 300 REM ---------- TEIL 2 ------------- 310 REM 320 REM *** 189 ZEICHEN IN DEN BILD- 330 REM *** SCHIRMSPEICHER POKEN. 340 FOR T=0 TO188:POKE 4096+T,T 350 POKE 37888+T,6:NEXT 360 REM 370 REM ---------- TEIL 3 ------------- 380 REM 390 REM *** HIRESSCREEN LOESCHEN 400 FOR T=0 TO3024:POKE 5120+T,0:NEXT 410 REM 420 REM ---------- TEIL 4 ------------- 430 REM 440 REM 450 REM *** HIER WURDE ALS DEMON- 460 REM *** STRATIONSBEISPIEL EINE 470 REM *** SIN-FUNKTION EINGESETZT. 480 FOR X=0 TO167 490 Y=(SIN (X*2*π/167)+1)*71.7 500 GOSUB 640 510 NEXT 520 GOTO 520 530 REM 540 REM ---------- TEIL 5 ------------- 550 REM 560 REM *** BITMAPPINGROUTINE 570 REM *** ================= 580 REM *** DIE HOCHAUFLOESENDEN PIXELS 590 REM *** KOENNEN UEBER KOORDINATEN 600 REM *** ANGESPROCHEN WERDEN. 610 REM *** DIE X-KOORDINATE MUSS <168, 620 REM *** Y MUSS <144 SEIN. 630 REM 640 ZX=INT (X/8) : PX=X-ZX*8 650 ZY=INT (Y/16): PY=Y-ZY*16 660 REM *** DIE KOORDINATEN WERDEN IN 670 REM *** EINEN ZEICHEN- UND EINEN 680 REM *** PIXELANTEIL AUFGESPALTEN. 690 AD=5120 +ZX*16 +ZY*336 +PY 700 REM *** AD IST DIE ZEILENADRESSE 710 REM *** EINES CHATNRAKTERS IM ZEI- 720 REM *** CHENGENERAROR RAM. 730 POKE AD,PEEK (AD) OR (2^ (7-PX)) 740 REM *** IN DIESER ZEILE WIRD DAS 750 REM *** GEWUENSCHTE PIXEL GESETZT. 760 RETURN
100 rem *** joypaint teil 1
110 rem >> vor dem laden <<
120 rem poke 44,39:poke9984,0
130 rem >> eingeben <<
140 fort=8192to9015:readd:s=s+d:poket,d:next
150 ifs<>92869thenprint"{clr}{down}{down}{down}fehler in datas !!":end
160 print"bitte teil 2 laden"
170 data 095,234,152,072,165,197,162,003
180 data 221,059,032,240,005,202,016,248
190 data 208,005,189,063,032,208,027,162
200 data 001,221,067,032,240,005,202,016
210 data 248,208,005,189,069,032,208,004
220 data 169,000,240,006,172,141,002,208
230 data 001,010,133,184,104,168,234,234
240 data 165,184,096,041,018,026,049,004
250 data 008,002,001,023,031,004,001,120
260 data 152,072,169,000,141,019,145,169
270 data 127,141,034,145,173,032,145,041
280 data 128,073,128,074,074,074,074,133
290 data 184,169,255,141,034,145,173,017
300 data 145,041,060,073,060,074,074,133
310 data 185,041,008,074,074,074,133,250
320 data 165,185,041,007,005,184,170,104
330 data 168,138,088,096,169,059,141,015
340 data 144,162,000,189,160,032,032,210
350 data 255,232,208,247,189,160,033,240
360 data 006,032,210,255,232,208,245,096
370 data 147,031,206,163,163,205,032,032
380 data 032,206,163,165,032,207,165,013
390 data 165,207,208,186,032,032,206,206
400 data 165,165,032,204,165,013,165,165
410 data 032,032,032,206,206,032,165,165
420 data 032,032,032,206,163,163,205,167
430 data 208,206,208,013,165,163,163,205
440 data 032,165,204,164,165,204,032,032
450 data 032,165,207,208,167,167,032,164
460 data 186,013,165,207,208,167,032,165
470 data 032,032,032,167,032,032,032,165
480 data 163,163,167,167,032,165,013,165
490 data 204,186,167,032,163,163,163,165
500 data 207,032,032,032,165,207,163,163
510 data 167,032,165,013,205,164,164,206
520 data 032,032,032,032,204,165,032,032
530 data 032,205,163,163,208,167,032,165
540 data 013,032,032,032,032,032,032,032
550 data 032,032,032,032,032,032,032,163
560 data 163,163,032,163,013,017,017,018
570 data 032,032,032,032,032,032,032,032
580 data 032,032,032,032,032,032,032,032
590 data 032,032,032,032,032,032,032,032
600 data 032,074,079,089,083,084,073,067
610 data 075,032,080,065,073,078,084,069
620 data 082,032,032,032,032,032,032,032
630 data 032,032,032,032,032,032,032,032
640 data 032,032,032,032,032,032,032,032
650 data 032,032,013,017,017,144,032,040
660 data 067,041,032,049,057,056,052,032
670 data 032,066,089,032,067,046,083,065
680 data 085,069,082,013,017,017,029,029
690 data 029,029,029,018,156,032,032,032
700 data 084,065,083,084,069,032,032,032
710 data 013,000,169,013,141,000,144,169
720 data 044,141,001,144,169,021,141,002
730 data 144,169,019,141,003,144,169,205
740 data 141,005,144,162,189,138,157,000
750 data 016,169,006,157,000,148,202,224
760 data 255,208,242,096,169,020,133,177
770 data 169,000,133,176,160,000,145,176
780 data 230,176,208,002,230,177,166,177
790 data 224,032,208,242,096,134,176,132
800 data 177,138,041,248,133,178,165,176
810 data 056,229,178,133,180,165,177,041
820 data 240,133,179,165,177,056,229,179
830 data 133,181,169,000,133,176,133,182
840 data 169,020,133,177,162,021,165,179
850 data 032,083,034,202,208,248,165,178
860 data 024,010,168,169,000,101,182,133
870 data 182,152,032,083,034,169,000,133
880 data 182,165,181,032,083,034,056,169
890 data 007,229,180,170,240,009,169,001
900 data 010,202,208,252,133,182,096,169
910 data 001,208,249,024,101,176,133,176
920 data 165,182,101,177,133,177,096,032
930 data 245,033,160,000,177,176,005,182
940 data 145,176,096,032,245,033,160,000
950 data 165,182,073,255,049,176,145,176
960 data 096,032,245,033,160,000,177,176
970 data 037,182,197,182,208,002,160,001
980 data 096,160,048,032,071,032,165,250
990 data 208,008,136,208,246,160,000,132
1000 data 069,096,169,240,141,012,144,160
1010 data 037,162,255,234,234,234,234,234
1020 data 202,208,248,136,208,243,160,255
1030 data 032,071,032,165,250,208,013,136
1040 data 208,246,160,001,132,069,169,000
1050 data 141,012,144,096,169,144,141,012
1060 data 144,160,032,162,255,234,234,202
1070 data 208,251,136,208,246,160,002,208
1080 data 227,169,015,141,014,144,032,137
1090 data 034,192,000,240,006,165,069,201
1100 data 002,240,001,096,169,000,141,014
1110 data 144,032,137,034,192,002,240,249
1120 data 160,002,132,069,208,237,165,197
1130 data 201,039,240,009,201,047,240,014
1140 data 160,000,132,069,096,169,240,032
1150 data 032,035,160,001,208,007,169,144
1160 data 032,032,035,160,002,132,069,096
1170 data 141,012,144,169,015,141,014,144
1180 data 160,037,162,255,234,234,202,208
1190 data 251,136,208,246,169,000,141,012
100 REM *** JOYPAINT TEIL 1 110 REM >> VOR DEM LADEN << 120 REM POKE 44,39:POKE9984,0 130 REM >> EINGEBEN << 140 FOR T=8192 TO9015:READ D:S=S+D:POKE T,D:NEXT 150 IF S<>92869 THENPRINT"{CLR,3DOWN}FEHLER IN DATAS !!":END 160 PRINT"BITTE TEIL 2 LADEN" 170 DATA 095,234,152,072,165,197,162,003 180 DATA 221,059,032,240,005,202,016,248 190 DATA 208,005,189,063,032,208,027,162 200 DATA 001,221,067,032,240,005,202,016 210 DATA 248,208,005,189,069,032,208,004 220 DATA 169,000,240,006,172,141,002,208 230 DATA 001,010,133,184,104,168,234,234 240 DATA 165,184,096,041,018,026,049,004 250 DATA 008,002,001,023,031,004,001,120 260 DATA 152,072,169,000,141,019,145,169 270 DATA 127,141,034,145,173,032,145,041 280 DATA 128,073,128,074,074,074,074,133 290 DATA 184,169,255,141,034,145,173,017 300 DATA 145,041,060,073,060,074,074,133 310 DATA 185,041,008,074,074,074,133,250 320 DATA 165,185,041,007,005,184,170,104 330 DATA 168,138,088,096,169,059,141,015 340 DATA 144,162,000,189,160,032,032,210 350 DATA 255,232,208,247,189,160,033,240 360 DATA 006,032,210,255,232,208,245,096 370 DATA 147,031,206,163,163,205,032,032 380 DATA 032,206,163,165,032,207,165,013 390 DATA 165,207,208,186,032,032,206,206 400 DATA 165,165,032,204,165,013,165,165 410 DATA 032,032,032,206,206,032,165,165 420 DATA 032,032,032,206,163,163,205,167 430 DATA 208,206,208,013,165,163,163,205 440 DATA 032,165,204,164,165,204,032,032 450 DATA 032,165,207,208,167,167,032,164 460 DATA 186,013,165,207,208,167,032,165 470 DATA 032,032,032,167,032,032,032,165 480 DATA 163,163,167,167,032,165,013,165 490 DATA 204,186,167,032,163,163,163,165 500 DATA 207,032,032,032,165,207,163,163 510 DATA 167,032,165,013,205,164,164,206 520 DATA 032,032,032,032,204,165,032,032 530 DATA 032,205,163,163,208,167,032,165 540 DATA 013,032,032,032,032,032,032,032 550 DATA 032,032,032,032,032,032,032,163 560 DATA 163,163,032,163,013,017,017,018 570 DATA 032,032,032,032,032,032,032,032 580 DATA 032,032,032,032,032,032,032,032 590 DATA 032,032,032,032,032,032,032,032 600 DATA 032,074,079,089,083,084,073,067 610 DATA 075,032,080,065,073,078,084,069 620 DATA 082,032,032,032,032,032,032,032 630 DATA 032,032,032,032,032,032,032,032 640 DATA 032,032,032,032,032,032,032,032 650 DATA 032,032,013,017,017,144,032,040 660 DATA 067,041,032,049,057,056,052,032 670 DATA 032,066,089,032,067,046,083,065 680 DATA 085,069,082,013,017,017,029,029 690 DATA 029,029,029,018,156,032,032,032 700 DATA 084,065,083,084,069,032,032,032 710 DATA 013,000,169,013,141,000,144,169 720 DATA 044,141,001,144,169,021,141,002 730 DATA 144,169,019,141,003,144,169,205 740 DATA 141,005,144,162,189,138,157,000 750 DATA 016,169,006,157,000,148,202,224 760 DATA 255,208,242,096,169,020,133,177 770 DATA 169,000,133,176,160,000,145,176 780 DATA 230,176,208,002,230,177,166,177 790 DATA 224,032,208,242,096,134,176,132 800 DATA 177,138,041,248,133,178,165,176 810 DATA 056,229,178,133,180,165,177,041 820 DATA 240,133,179,165,177,056,229,179 830 DATA 133,181,169,000,133,176,133,182 840 DATA 169,020,133,177,162,021,165,179 850 DATA 032,083,034,202,208,248,165,178 860 DATA 024,010,168,169,000,101,182,133 870 DATA 182,152,032,083,034,169,000,133 880 DATA 182,165,181,032,083,034,056,169 890 DATA 007,229,180,170,240,009,169,001 900 DATA 010,202,208,252,133,182,096,169 910 DATA 001,208,249,024,101,176,133,176 920 DATA 165,182,101,177,133,177,096,032 930 DATA 245,033,160,000,177,176,005,182 940 DATA 145,176,096,032,245,033,160,000 950 DATA 165,182,073,255,049,176,145,176 960 DATA 096,032,245,033,160,000,177,176 970 DATA 037,182,197,182,208,002,160,001 980 DATA 096,160,048,032,071,032,165,250 990 DATA 208,008,136,208,246,160,000,132 1000 DATA 069,096,169,240,141,012,144,160 1010 DATA 037,162,255,234,234,234,234,234 1020 DATA 202,208,248,136,208,243,160,255 1030 DATA 032,071,032,165,250,208,013,136 1040 DATA 208,246,160,001,132,069,169,000 1050 DATA 141,012,144,096,169,144,141,012 1060 DATA 144,160,032,162,255,234,234,202 1070 DATA 208,251,136,208,246,160,002,208 1080 DATA 227,169,015,141,014,144,032,137 1090 DATA 034,192,000,240,006,165,069,201 1100 DATA 002,240,001,096,169,000,141,014 1110 DATA 144,032,137,034,192,002,240,249 1120 DATA 160,002,132,069,208,237,165,197 1130 DATA 201,039,240,009,201,047,240,014 1140 DATA 160,000,132,069,096,169,240,032 1150 DATA 032,035,160,001,208,007,169,144 1160 DATA 032,032,035,160,002,132,069,096 1170 DATA 141,012,144,169,015,141,014,144 1180 DATA 160,037,162,255,234,234,202,208 1190 DATA 251,136,208,246,169,000,141,012
100 rem *** joypaint teil 2
110 rem >> vor dem laden <<
120 rem >> poke 44,39 eingeben <<
130 fort=9016to9825:readd:s=s+d:poket,d:next
140 ifs<>93663thenprint"{clr}{down}{down}{down}fehler in datas !!":end
150 sys9682
160 data 144,141,014,144,096,032,178,033
170 data 169,000,170,149,064,232,224,006
180 data 208,249,170,168,032,095,034,032
190 data 217,034,208,003,032,254,034,208
200 data 124,032,016,036,032,071,032,208
210 data 009,032,002,032,208,004,169,000
220 data 240,229,133,183,165,068,240,007
230 data 032,098,034,169,000,240,003,032
240 data 110,034,166,183,189,249,035,168
250 data 189,239,035,024,101,064,201,255
260 data 240,006,201,166,176,006,208,006
270 data 169,000,240,002,169,166,133,064
280 data 133,065,170,024,152,101,066,201
290 data 255,240,006,201,143,176,006,208
300 data 006,169,000,240,002,169,143,133
310 data 066,133,067,168,032,121,034,133
320 data 068,168,240,007,032,110,034,169
330 data 000,240,003,032,098,034,164,050
340 data 032,042,035,165,070,240,128,169
350 data 000,133,070,240,132,165,069,201
360 data 002,240,014,169,008,162,001,134
370 data 068,133,183,169,001,133,070,208
380 data 131,162,000,169,004,208,240,234
390 data 000,000,000,255,255,255,000,001
400 data 001,001,255,001,000,000,255,001
410 data 000,000,255,001,000,000,000,000
420 data 000,000,000,000,000,000,000,000
430 data 173,141,002,201,001,240,006,165
440 data 053,048,002,133,068,173,141,002
450 data 201,004,240,018,165,197,201,024
460 data 208,003,076,211,036,201,055,240
470 data 067,201,063,240,068,096,173,015
480 data 144,133,055,169,008,141,015,144
490 data 165,197,162,021,221,079,038,240
500 data 016,202,208,248,173,141,002,201
510 data 004,240,237,165,055,141,015,144
520 data 096,138,010,170,234,189,084,038
530 data 133,048,189,085,038,133,049,165
540 data 055,141,015,144,160,144,032,042
550 data 035,108,048,000,169,003,133,050
560 data 096,169,043,208,249,169,004,141
570 data 014,144,169,160,141,011,144,173
580 data 015,144,133,051,141,015,144,165
590 data 197,201,064,240,250,201,005,240
600 data 010,201,061,240,010,201,015,240
610 data 032,208,236,169,001,208,002,169
620 data 255,133,052,165,051,024,101,052
630 data 133,051,160,048,162,255,234,234
640 data 234,202,208,250,136,208,245,240
650 data 203,169,000,141,011,144,141,014
660 data 144,096,169,001,133,053,096,169
670 data 000,240,249,169,255,208,245,165
680 data 068,240,007,032,098,034,169,000
690 data 240,003,032,110,034,032,024,229
700 data 096,032,178,033,076,195,035,169
710 data 000,133,198,032,215,036,162,000
720 data 189,255,037,032,210,255,232,224
730 data 017,208,245,162,000,032,015,225
740 data 201,013,240,008,157,000,002,232
750 data 224,016,144,241,134,250,162,000
760 data 189,016,038,032,210,255,232,224
770 data 049,208,245,032,228,255,240,251
780 data 201,049,240,006,201,050,240,006
790 data 208,241,162,001,208,002,162,008
800 data 134,251,169,000,133,193,133,172
810 data 133,174,169,020,133,194,133,173
820 data 169,032,133,175,165,250,133,183
830 data 169,000,133,187,169,002,133,188
840 data 165,251,133,186,032,249,253,169
850 data 060,133,178,169,003,133,179,096
860 data 032,239,036,032,130,246,032,134
870 data 037,076,233,036,032,239,036,166
880 data 193,164,194,169,000,032,066,245
890 data 032,134,037,076,233,036,169,013
900 data 032,210,255,165,251,201,001,240
910 data 032,169,008,032,180,255,169,111
920 data 032,150,255,032,165,255,201,013
930 data 240,006,032,066,231,184,080,243
940 data 032,066,231,032,171,255,024,144
950 data 012,032,183,255,240,007,169,105
960 data 160,195,032,030,203,169,008,133
970 data 255,162,255,160,255,234,234,136
980 data 208,251,202,208,246,198,255,208
990 data 240,096,032,132,032,032,228,255
1000 data 201,000,240,249,169,027,141,015
1010 data 144,169,037,133,050,169,255,133
1020 data 053,165,254,201,210,240,003,032
1030 data 220,033,169,210,133,254,076,061
1040 data 035,234,234,234,234,234,234,234
1050 data 147,017,018,070,073,076,069,013
1060 data 018,078,065,077,069,058,146,032
1070 data 013,017,017,018,068,069,086,073
1080 data 067,069,058,146,032,049,046,032
1090 data 084,065,080,069,032,032,032,040
1100 data 049,041,013,032,032,032,032,032
1110 data 032,032,032,050,046,032,070,076
1120 data 079,080,080,089,032,040,056,041
1130 data 013,017,017,070,079,080,080,089
1140 data 032,069,082,082,079,082,058,032
1150 data 034,042,041,021,039,047,220,033
1160 data 125,036,104,037,116,037,202,036
1170 data 207,036
100 REM *** JOYPAINT TEIL 2 110 REM >> VOR DEM LADEN << 120 REM >> POKE 44,39 EINGEBEN << 130 FOR T=9016 TO9825:READ D:S=S+D:POKE T,D:NEXT 140 IF S<>93663 THENPRINT"{CLR,3DOWN}FEHLER IN DATAS !!":END 150 SYS 9682 160 DATA 144,141,014,144,096,032,178,033 170 DATA 169,000,170,149,064,232,224,006 180 DATA 208,249,170,168,032,095,034,032 190 DATA 217,034,208,003,032,254,034,208 200 DATA 124,032,016,036,032,071,032,208 210 DATA 009,032,002,032,208,004,169,000 220 DATA 240,229,133,183,165,068,240,007 230 DATA 032,098,034,169,000,240,003,032 240 DATA 110,034,166,183,189,249,035,168 250 DATA 189,239,035,024,101,064,201,255 260 DATA 240,006,201,166,176,006,208,006 270 DATA 169,000,240,002,169,166,133,064 280 DATA 133,065,170,024,152,101,066,201 290 DATA 255,240,006,201,143,176,006,208 300 DATA 006,169,000,240,002,169,143,133 310 DATA 066,133,067,168,032,121,034,133 320 DATA 068,168,240,007,032,110,034,169 330 DATA 000,240,003,032,098,034,164,050 340 DATA 032,042,035,165,070,240,128,169 350 DATA 000,133,070,240,132,165,069,201 360 DATA 002,240,014,169,008,162,001,134 370 DATA 068,133,183,169,001,133,070,208 380 DATA 131,162,000,169,004,208,240,234 390 DATA 000,000,000,255,255,255,000,001 400 DATA 001,001,255,001,000,000,255,001 410 DATA 000,000,255,001,000,000,000,000 420 DATA 000,000,000,000,000,000,000,000 430 DATA 173,141,002,201,001,240,006,165 440 DATA 053,048,002,133,068,173,141,002 450 DATA 201,004,240,018,165,197,201,024 460 DATA 208,003,076,211,036,201,055,240 470 DATA 067,201,063,240,068,096,173,015 480 DATA 144,133,055,169,008,141,015,144 490 DATA 165,197,162,021,221,079,038,240 500 DATA 016,202,208,248,173,141,002,201 510 DATA 004,240,237,165,055,141,015,144 520 DATA 096,138,010,170,234,189,084,038 530 DATA 133,048,189,085,038,133,049,165 540 DATA 055,141,015,144,160,144,032,042 550 DATA 035,108,048,000,169,003,133,050 560 DATA 096,169,043,208,249,169,004,141 570 DATA 014,144,169,160,141,011,144,173 580 DATA 015,144,133,051,141,015,144,165 590 DATA 197,201,064,240,250,201,005,240 600 DATA 010,201,061,240,010,201,015,240 610 DATA 032,208,236,169,001,208,002,169 620 DATA 255,133,052,165,051,024,101,052 630 DATA 133,051,160,048,162,255,234,234 640 DATA 234,202,208,250,136,208,245,240 650 DATA 203,169,000,141,011,144,141,014 660 DATA 144,096,169,001,133,053,096,169 670 DATA 000,240,249,169,255,208,245,165 680 DATA 068,240,007,032,098,034,169,000 690 DATA 240,003,032,110,034,032,024,229 700 DATA 096,032,178,033,076,195,035,169 710 DATA 000,133,198,032,215,036,162,000 720 DATA 189,255,037,032,210,255,232,224 730 DATA 017,208,245,162,000,032,015,225 740 DATA 201,013,240,008,157,000,002,232 750 DATA 224,016,144,241,134,250,162,000 760 DATA 189,016,038,032,210,255,232,224 770 DATA 049,208,245,032,228,255,240,251 780 DATA 201,049,240,006,201,050,240,006 790 DATA 208,241,162,001,208,002,162,008 800 DATA 134,251,169,000,133,193,133,172 810 DATA 133,174,169,020,133,194,133,173 820 DATA 169,032,133,175,165,250,133,183 830 DATA 169,000,133,187,169,002,133,188 840 DATA 165,251,133,186,032,249,253,169 850 DATA 060,133,178,169,003,133,179,096 860 DATA 032,239,036,032,130,246,032,134 870 DATA 037,076,233,036,032,239,036,166 880 DATA 193,164,194,169,000,032,066,245 890 DATA 032,134,037,076,233,036,169,013 900 DATA 032,210,255,165,251,201,001,240 910 DATA 032,169,008,032,180,255,169,111 920 DATA 032,150,255,032,165,255,201,013 930 DATA 240,006,032,066,231,184,080,243 940 DATA 032,066,231,032,171,255,024,144 950 DATA 012,032,183,255,240,007,169,105 960 DATA 160,195,032,030,203,169,008,133 970 DATA 255,162,255,160,255,234,234,136 980 DATA 208,251,202,208,246,198,255,208 990 DATA 240,096,032,132,032,032,228,255 1000 DATA 201,000,240,249,169,027,141,015 1010 DATA 144,169,037,133,050,169,255,133 1020 DATA 053,165,254,201,210,240,003,032 1030 DATA 220,033,169,210,133,254,076,061 1040 DATA 035,234,234,234,234,234,234,234 1050 DATA 147,017,018,070,073,076,069,013 1060 DATA 018,078,065,077,069,058,146,032 1070 DATA 013,017,017,018,068,069,086,073 1080 DATA 067,069,058,146,032,049,046,032 1090 DATA 084,065,080,069,032,032,032,040 1100 DATA 049,041,013,032,032,032,032,032 1110 DATA 032,032,032,050,046,032,070,076 1120 DATA 079,080,080,089,032,040,056,041 1130 DATA 013,017,017,070,079,080,080,089 1140 DATA 032,069,082,082,079,082,058,032 1150 DATA 034,042,041,021,039,047,220,033 1160 DATA 125,036,104,037,116,037,202,036 1170 DATA 207,036
100 rem ********************************
110 rem *** ***
120 rem *** multicolor-figur fuer ***
130 rem *** alle ausbauversionen ***
140 rem *** ***
150 rem ********************************
160 print"{clr}"
170 fort=0to7:readd:poke7168+t,d:next
180 pokepeek(648)*256+69,0
190 rem *** @ in bildschirmposition
200 poke 38469,10
210 rem *** bei 8 kbyte erweiterung
220 rem *** den poke durch 37957,10
230 poke36869,peek(36869)or15
240 rem *** zeichengenerator ins ram
250 goto250
260 data48,68,204,48,100,48,48,136
100 REM ******************************** 110 REM *** *** 120 REM *** MULTICOLOR-FIGUR FUER *** 130 REM *** ALLE AUSBAUVERSIONEN *** 140 REM *** *** 150 REM ******************************** 160 PRINT"{CLR}" 170 FOR T=0 TO7:READ D:POKE 7168+T,D:NEXT 180 POKE PEEK (648)*256+69,0 190 REM *** @ IN BILDSCHIRMPOSITION 200 POKE 38469,10 210 REM *** BEI 8 KBYTE ERWEITERUNG 220 REM *** DEN POKE DURCH 37957,10 230 POKE 36869,PEEK (36869)OR 15 240 REM *** ZEICHENGENERATOR INS RAM 250 GOTO 250 260 DATA 48,68,204,48,100,48,48,136
