Assembler ist keine Alchimie — Teil 9
Multiplizieren und Dividieren größerer Zahlen ist weder mit dem Taschenrechner noch in Basic ein Problem. Mit Assembler sieht die Sache anfangs schon nicht mehr so einfach aus. Doch auch diese Hürde wird genommen. Einige Betriebssystemroutinen des C 64 nehmen uns dabei erhebliche Arbeit ab, man muß sie nur kennen.
Einige Versprechen sollen diesmal eingelöst werden:
Die restlichen Bit-Verschiebe-Befehle werden Ihnen vorgestellt und auch gleich ein paar Anwendungen wie die 16-Bit-Multiplikation und auch die 16-Bit-Division. Außerdem soll endlich das Programmprojekt weitergeführt werden. Diesmal erzeugen wir einen Hilfsbildschirm und legen ihn abrufbereit unter den oberen ROM-Bereich. Bei der Gelegenheit lernen Sie auch gleich noch ein paar Interpreter-Routinen kennen.
Die restlichen Bit-Verschiebe-Operationen
Da wäre zunächst einmal das Gegenstück zu ASL. Den Befehl haben wir in der letzten Ausgabe kennengelernt. Dort ging es ja um das Nach-Links-Schieben. Jetzt schieben wir nach rechts. LSR heißt der dazu nötige Befehl. Das kommt von »logical shift right« und heißt zu deutsch »logisches Rechtsschieben«. Fragen Sie mich bitte nicht, weshalb »logisches«. Jedenfalls ist LSR ebenso für logische Bitprüfungen geeignet wie ASL.
Mittels LSR wird jedes Bit der adressierten Speicherstelle um einen Platz nach rechts geschoben. An die Stelle des Bit 7 tritt eine Null und Bit 0 wandert in das Carry-Bit (siehe Bild 1).

Erinnern Sie sich noch an das dezimale Linksschieben mit ASL aus der letzten Folge? Wir hatten festgestellt, daß jedes Linksschieben einer Dezimalzahl einer Multiplikation mit 10 entspricht. Hier im umgekehrten Fall, also beim Rechtsschieben, muß jedes LSR einer Division durch 10 entsprechen:
| 25000 | wird durch LSR zu | 2500 |
| 2500 | 250 | |
| 250 | 25 | |
| und so weiter | ||
Geht man von der Ausgangszahl (25000) aus, dann ergibt sich der erste rechts verschobene Wert durch Division mit
| 101=10 | |
| der 2. durch | 102=100 |
| der 3. durch | 103=1000 |
Es wird also durch Potenzen der Zahlenbasis 10 geteilt. Haben wir es — wie im Computer — mit Binärzahlen zu tun, deren Basis die 2 ist, dann teilen wir mit jedem LSR durch 2. Je nachdem, wie oft hintereinander das LSR auf eine Zahl ausgeübt wird, teilt man dann durch 21=2, 22=4, 23 = 8, etc. Das konnte man sich alles ja schon vorstellen, nachdem ASL zur Multiplikation verwendet wurde. Auch hier muß man immer das Carry-Bit abfragen, denn die Division kann ja unter Umständen nicht aufgehen, wie das folgende Beispiel der Division von 3 durch 2 zeigt:
(3) 0000 0011 ergibt durch LSR: 0000 0001 und 1 im Carry-Bit. Das Ergebnis ist schon richtig, nämlich 1. Im Carry steht der Rest dieser Division, die 1. Weil der Rest für manche Berechnungen von Bedeutung ist, muß das Carry-Bit irgendwie erfaßt werden. Wie man das erreicht, lernen wir später noch. Leider ist diese Art der Division mittels LSR nicht so einfach verwendbar wie die Multiplikation mittels ASL. Während man dort durch geschicktes Aufteilen des Faktors ASL auch bei anderen Multiplikatoren als reine Zweierpotenzen anwenden konnte, ist das hier nicht so ohne weiteres möglich. Bei Divisionen geht man deshalb lieber andere Wege. Die zeige ich Ihnen ebenfalls etwas später.
LSR kann auf die gleiche Weise adressiert werden wie ASL:
| LSR | auf den Akku bezogen |
| LSR 6000 | absolut |
| LSR FE | Zeropage-absolut |
| LSR 6000,X | absolut-X-indiziert |
| LSR FA,X | Zeropage-absolut-X-indiziert |
Im ersten Fall steht das Ergebnis im Akku, in den anderen Fällen in der jeweils adressierten Speicherstelle. Außer der N-Flagge, die in jedem Fall 0 wird, beeinflußt LSR auch die Carry-Flagge und unter Umständen die Z-Flagge. Je nach Adressierungsart liegt LSR als 1-Byte-, 2-Byte- oder 3-Byte-Befehl vor.
Sowohl bei ASL als auch bei LSR hatten wir festgestellt, daß man herausgeschobene Bits, falls sie noch von Bedeutung sind, irgendwie aus dem Carry-Bit (dort sind sie ja gelandet) an einen sinnvollen Ort schaffen muß. Das ist natürlich möglich über eine Befehlskette, in der zunächst das Carry-Bit abgefragt wird:
zum Beispiel:
| 6000 | BCC 6007 |
| 6002 | LDA #01 |
| 6004 | STA 8000 |
| 6007 | etc. |
Wenn das Carry-Bit frei ist, wird alles weitere übersprungen. Wenn da drin etwas aufgetaucht ist, lädt man eine 1 (die ist ja im Carry-Bit) an die benötigte Speicherstelle (hier zum Beispiel 8000). Das kostet aber einige Bytes Speicherplatz und einige Taktzeiten Rechendauer. Außerdem erschwert sich die Programmierung, wenn man eine Zahl öfter verschiebt und dann nach 8000 alle Carry-Inhalte packen will. So kompliziert brauchen wir auch gar nicht zu arbeiten, denn unsere CPU kennt zwei Befehle, die das Bit-Verschieben und das Carry-Verschieben für uns machen. Das sind:
| ROL rotate left | Linksrotieren |
| ROR rotate right | Rechtsrotieren |
Sehen wir uns zunächst mal ROL (Bild 2) an:
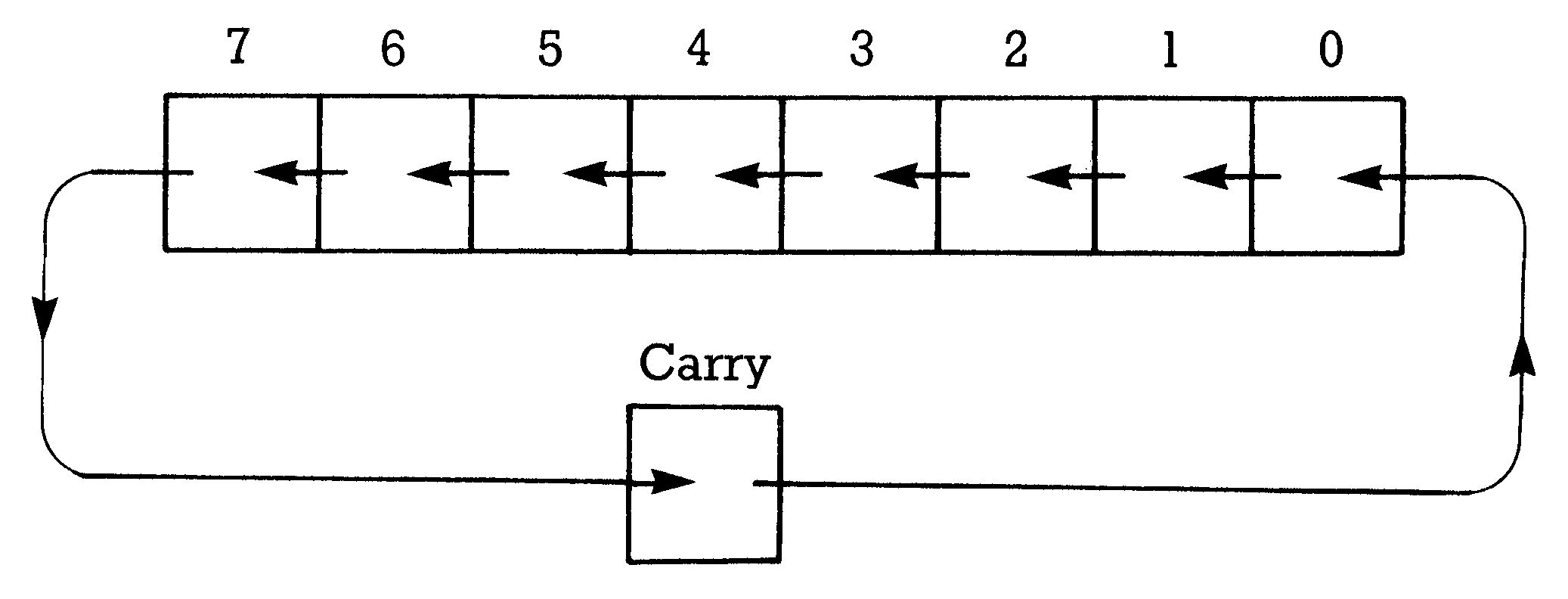
Wie bei ASL wandert jedes Bit um eine Position nach links. Das Bit 7 wird dabei in das Carry-Bit verschoben. In Bit 0 gelangt aber hier nicht eine 0 (wie bei ASL), sondern der Inhalt des Carry-Bit (wohlgemerkt der Inhalt, der dort war, bevor dort hinein Bit 7 geschoben wurde). Bevor wir auf den praktischen Nährwert dieses Befehls eingehen, sollen erstmal die Adressierungsmöglichkeiten aufgeführt werden:
| ROL | auf den Akku bezogen |
| ROL 6000 | absolut |
| ROL FE | Zeropage-absolut |
| ROL 6000,X | absolut-X-indiziert |
| ROL FE,X | Zeropage-absolut-X-indiziert |
Je nach Adressierung kann es sich dann wieder um einen 1-Byte- bis 3-Byte-Befehl handeln. Die N-, Z- und natürlich die Carry-Flagge sind beeinflußt und das Ergebnis des Befehls ist im Akku zu finden (erste Adressierungsart) oder in der angesprochenen Speicherstelle.
Wozu das Ganze? Abgesehen von der Möglichkeit, einzelne Bits auf diese Weise ohne Verlust aus einem Byte durch das Carry-Bit herausschieben zu können, um sie Prüfungen zu unterziehen, gibt es noch die Möglichkeit, einen Überlauf bei Rechenoperationen aufzufangen. Erinnern Sie sich an die letzte Folge, wo wir mittels ASL Multiplikationen durchgeführt hatten? Dort kann es unter gewissen Umständen ja leicht geschehen, daß ein Byte für das Ergebnis nicht mehr ausreicht. Wir haben in den Beispielen schon die Überlegung durchgeführt, daß man mittels BCC oder BCS prüfen sollte, ob man eine signifikante Stelle (also eine führende 1) aus dem Byte herausgeschoben hat. Ist das der Fall, dann gibt es zwei Wege:
- Man veranlaßt den Ausdruck eines OVERFLOW ERROR, wenn nur 1-Byte-Zahlen zulässig sind, oder
- man schaltet um auf 2-Byte-Zahlen.
Sehen wir uns das mal an dem Schritt 7 des Beispiels aus der letzten Folge an. Dort hatten wir die Zahl 192 (binär 1100 0000) vorliegen (zum Beispiel in Speicherstelle 7000). Im Computer werden 2-Byte-Integers in der Form LSB/MSB verarbeitet. Wir schaffen also die Speicherstelle für das MSB von 192 in 7001. Jetzt muß dort noch 0 drin stehen. Um bei nochmaliger Multiplikation mit 2 eine 16-Bit-Zahl als Ergebnis zu erhalten, verfährt man wie folgt:
| 6000 | ASL 7000 | Damit ist die führende 1 ins Carry-Bit gewandert |
| 6003 | BCC 6008 | Das setzt man natürlich nur dann ein, wenn man nicht genau weiß, welches Ergebnis zu erwarten ist. Wenn keine 1 ins Carry-Bit gelangte, kann man die nächste Zeile überspringen. |
| 6005 | ROL 7001 | Damit wurde der Inhalt des Carry-Bit als Bit 0 ins MSB unseres Ergebnisses geschoben. |
| 6008 | etc. |
Die Funktion dieser Befehlssequenz können Sie aus Bild 3 entnehmen.

Diesem Befehl werden wir später bei der 16-Bit-Multiplikation und Division noch häufig begegnen.
Sehen wir uns nun noch den letzten der Bit-Verschiebebefehle an: ROR. In Bild 4 ist schematisch gezeigt, wie rotiert wird.
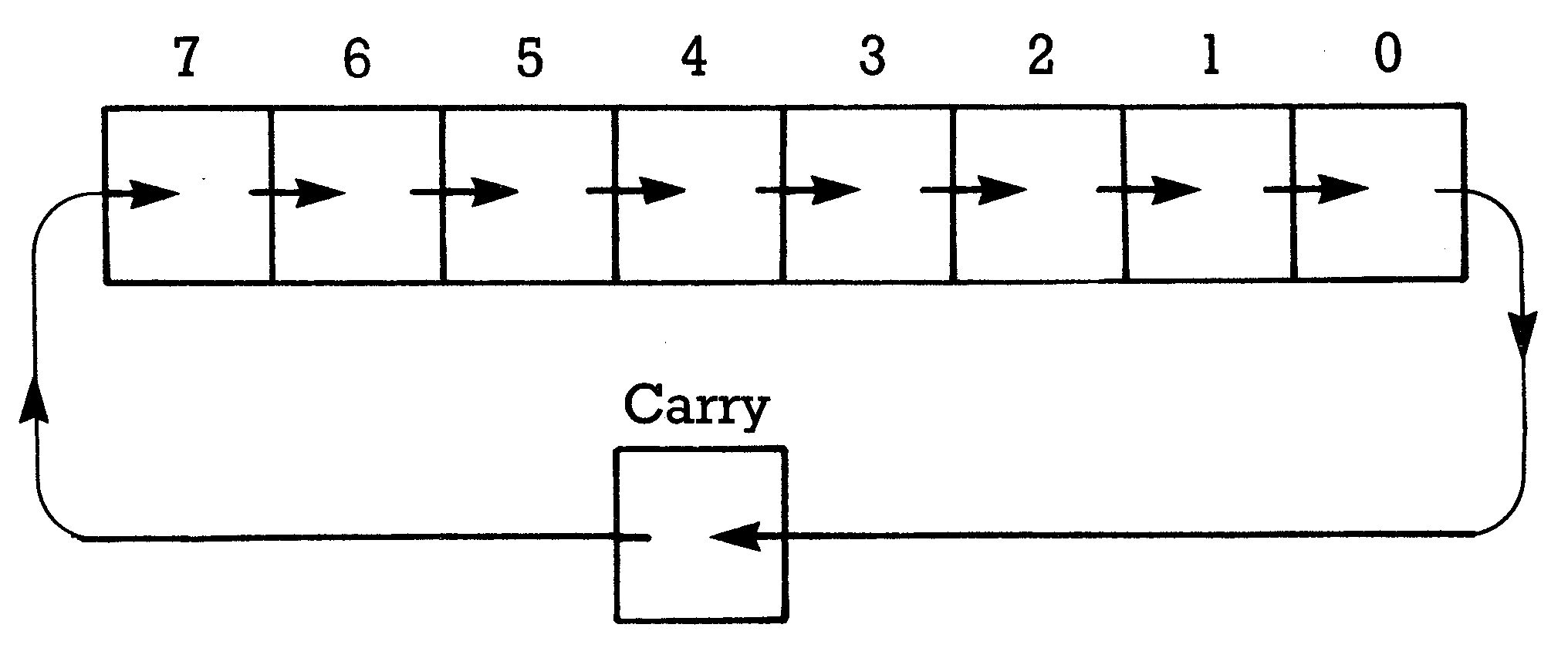
Jedes Bit wandert, wie bei LSR, um eine Stelle nach rechts. Als Bit 7 kommt (im Gegensatz zu LSR) der Inhalt des Carry-Bit herein. Bit 0 wird ins Carry-Bit geschoben. Adressiert werden kann ROR ebenso wie ROL:
| ROR | auf den Akku bezogen |
| ROR 6000 | absolut |
| ROR FE | Zeropage-absolut |
| ROR 6000,X | absolut-X-indiziert |
| ROR FE,X | Zeropage-absolut-X-indiziert |
Auch für die Byteanzahl, den Ort des Ergebnisses und die Flaggenbeanspruchung gilt dasselbe wie für ROL.
Die Einsatzmöglichkeiten für ROR sind allerings geringer. Bei 16-Bit-Divisionen kann man zwar ROR einsetzen, um einen Unterlauf des MSB ins LSB aufzufangen. Weil man aber meist ohnehin andere Divisionsverfahren verwendet als das oben gezeigte mit LSR, erübrigt sich diese Anwendung in den meisten Fällen. Gut kann man ROR zu Bitprüfungen einsetzen. Das soll im nächsten Abschnitt an einem kleinen Beispiel gezeigt werden.
Zuvor aber noch eine Bemerkung: Wir sind nun durch den Befehlssatz des 6502-Assemblers fast hindurchgedrungen. Es fehlen uns nur noch — wenn ich mich nicht versehen habe — vier Befehle. Die allerdings hängen eng mit dem sogenannten Interrupthandling zusammen, das uns wohl einige Zeit beschäftigen wird.
Schneller Joystick
Vor einiger Zeit (64’er, Ausgabe 2/85) veröffentlichte P. Siepen eine Routine zur Abfrage des Joystickports, die eine interessante Leserbrief-Reaktion hervorrief. M. Hartig sandte nämlich einen Verbesserungsvorschlag, in dem der uns interessierende Befehl ROR die Hauptrolle spielt. Bevor ich die allerdings vorstelle, muß erst noch geklärt werden, was und wie abgefragt wird.
Signale vom Joystick landen in den DATA-Ports A oder B des CIA 1. CIA heißt »Complex Interface Adapter« und ist die Institution unseres Computers, die den Verkehr mit der Außenwelt erlaubt. Wir haben zwei Stück davon (CIA 1 und CIA 2). Je nachdem, in welchen Port der Joystick gesteckt wurde, laufen die Signale in den Registern DC00 oder DC01 (dezimal 56320 oder 56321) ein. Wir nehmen im weiteren mal DC00 an. Die Bits 0 bis 4 beziehen sich auf den Joystick:
| Bit 0 | oben |
| Bit 1 | unten |
| Bit 2 | links |
| Bit 3 | rechts |
| Bit 4 | Feuerknopf |
Wenn keine dieser Möglichkeiten angesprochen ist, enthalten diese Bits den Wert 1. Drückt man beispielsweise den Feuerknopf, dann wechselt der Inhalt von Bit 4 zum Wert 0. Man muß also ständig diese Bits überprüfen und reagieren, sobald eines davon 0 wird. Die Lösung von P. Siepen, diese Abfrage in das Interruptprogramm einzubauen, ist sehr brauchbar. Dadurch hat der Computer die Möglichkeit, trotzdem an anderen Aufgaben weiterzuarbeiten. Wir werden in den nächsten Folgen auf diese Programmiertechnik eingehen. Die Verbesserung von M. Hartig besteht darin, daß er nicht durch CMP-Befehle den Inhalt von DC00 prüft (was Zeit und auch Speicherplatz kostet), sondern mittels ROR Bit für Bit nach rechts in das Carry-Bit schiebt und dieses dann mit BCC abfragt. Sobald die Carry-Flagge nämlich frei ist, ist die zu dem Bit gehörige Joystickfunktion gefragt.
Nun die Abfrageroutine:
| LDA DC00 | Inhalt des DATA-Port A in den Akku |
| ROR | Durch Rechtsrotieren wird Bit 0 in die Carry-Flagge geschoben. |
| BCC Oben | Wenn die Carry-Flagge nicht gesetzt ist, war Bit 0 eine Null, also die Joystickfunktion »Oben« gefordert, zu deren Bearbeitung hier verzweigt werden kann. |
| ROR | Das nächste Rechtsrotieren schiebt Bit 1 in die Carry-Flagge. |
| BCC Unten | Auch hier wieder Abzweigen zur Bearbeitung von »Unten«, wenn Bit 1 nicht gesetzt war. |
| ROR | Bit 2 ins Carry-Bit |
| BCC Links | und bearbeiten, wenn nicht gesetzt |
| ROR | Bit 3 in Carry-Flagge |
| BCC Rechts | und verzweigen wenn Bit 3 Null war |
| ROR | zu guter Letzt kommt noch Bit 4 ins Carry-Bit |
| BCC Fire | und kann bearbeitet werden, wenn es Null war. |
| .... weitere Bearbeitung, wenn keine Joystickfunktion | |
Der Vorteil dieser nur 18 Byte langen Unterroutine liegt in ihrer Schnelligkeit: Sie braucht nur 24 Taktzyklen, wenn nicht verzweigt wird, beziehungsweise 25, wenn verzweigt wird. Natürlich wäre anstelle von ROR auch die Verwendung von LSR möglich gewesen, denn die herausgeschobenen Bits werden nicht mehr benötigt. Im Falle, daß man nach einer solchen Abfrage wieder den Ausgangszustand des Akku oder der Speicherstelle herstellen will, muß man eine entsprechende Anzahl ROR-Anweisungen anschließen, bis Bit 0 wieder in seine Ausgangslage rotiert ist.
Die 16-Bit-Multiplikation
Wir haben in der letzten und in dieser Folge gelernt, wie man 8-Bit-Zahlen miteinander malnehmen kann um 8- oder 16-Bit-Zahlen zu erhalten. Dabei ist unbefriedigend, daß man sich über jede Zahl Gedanken machen muß, wie man sie am besten multipliziert. Was fehlt, ist ein allgemein gültiges Programm, das in der Lage ist, jede Zahlenkombination (solange es sich um 2-Byte-Integers handelt und das Ergebnis als 16-Bit-Zahl darstellbar ist) zu verarbeiten. Und da haben wir mal wieder Glück: Gut versteckt befindet sich so etwas bereits fertig in unserem Computer. Ab dez. 45900 ($B34C) liegt im Interpreter solch eine Routine und ihr Einsprungspunkt ist für uns bei dez. 45911 ($B357). Bevor wir aber detailliert darauf eingehen, soll noch das Prinzip erklärt werden, das dabei genutzt wird.
Jeden Tag rechnen Sie wahrscheinlich völlig automatisch Multiplikationsaufgaben, ohne noch Gedanken daran zu verschwenden, wieviel Schweiß das Erlernen dieser Technik früher mal gekostet hat. Könnten Sie heute noch jemandem genau erklären, warum man da was wie macht? Genau das müssen wir aber tun, damit der Binärautomat (unser C 64) multiplizieren lernt. Nehmen wir mal eine Multiplikation von 16x15:
| 16 x 15 |
| 16 |
| 80 |
| 240 |
Daß wir nicht so genau wissen, was wir da tun, liegt am ziemlich komplizierten Zehnersystem. Damit das alles einfacher und überschaubarer wird, wechseln wir mal ins Binärsystem: 16 = 10000, 15 = 1111. Die Aufgabe sieht dann so aus:
| 10000 * 1111 |
| 10000 |
| 10000 |
| 10000 |
| 10000 |
| 11110000 |
Jetzt wird schon deutlicher, was wir getan haben. Der Faktor auf der rechten Seite wurde vom MSB an Bit für Bit durchgesehen. Jedesmal, wenn wir auf eine 1 gestoßen sind (hier waren nur Einsen), haben wir den links stehenden Faktor notiert. Dabei sind wir von mal zu mal um eine Stelle nach rechts gerückt, was zu tun hat mit dem Stellenwert des im rechten Faktor gerade betrachteten Bits. Das geschah so lange, bis alle Bits des rechten Faktors durchgearbeitet waren. Die sich auf diese Weise ergebene Kolonne wird dann addiert und führt zum Ergebnis. Vergleichen Sie, 240 ist wirklich binär 1111 0000.
Genauso wie hier beschrieben, arbeitet das Multiplikationsprogramm. Ein Unterschied tritt auf, nämlich daß nicht bis zum Schluß mit der Addition gewartet, sondern jede neue Zwischenzahl sofort addiert wird. Bild 5a zeigt die Beschreibung der Interpreterroutine:
| Name | UMULT |
| Zweck | Multiplikation zweier 16-Bit-Zahlen |
| Adresse | $B357 dez. 45911 |
| Vorbereitungen | Faktor 1 in $28/29 Faktor 2 in $71/72 |
| Speicherstellen | $28/29,$71/72, $5D |
| Register | Akku, X- und Y-Register |
| Stapelbedarf | keiner |
Diese Routine hier abzudrucken, wäre reine Platzverschwendung. Schalten Sie einfach den SMON ein und verlangen Sie von ihm ein Disassemblerlisting ab B357. Dort haben Sie dann für die weitere Besprechung alles parat. In Bild 5 finden Sie noch ein Flußdiagramm der UMULT-Routine.
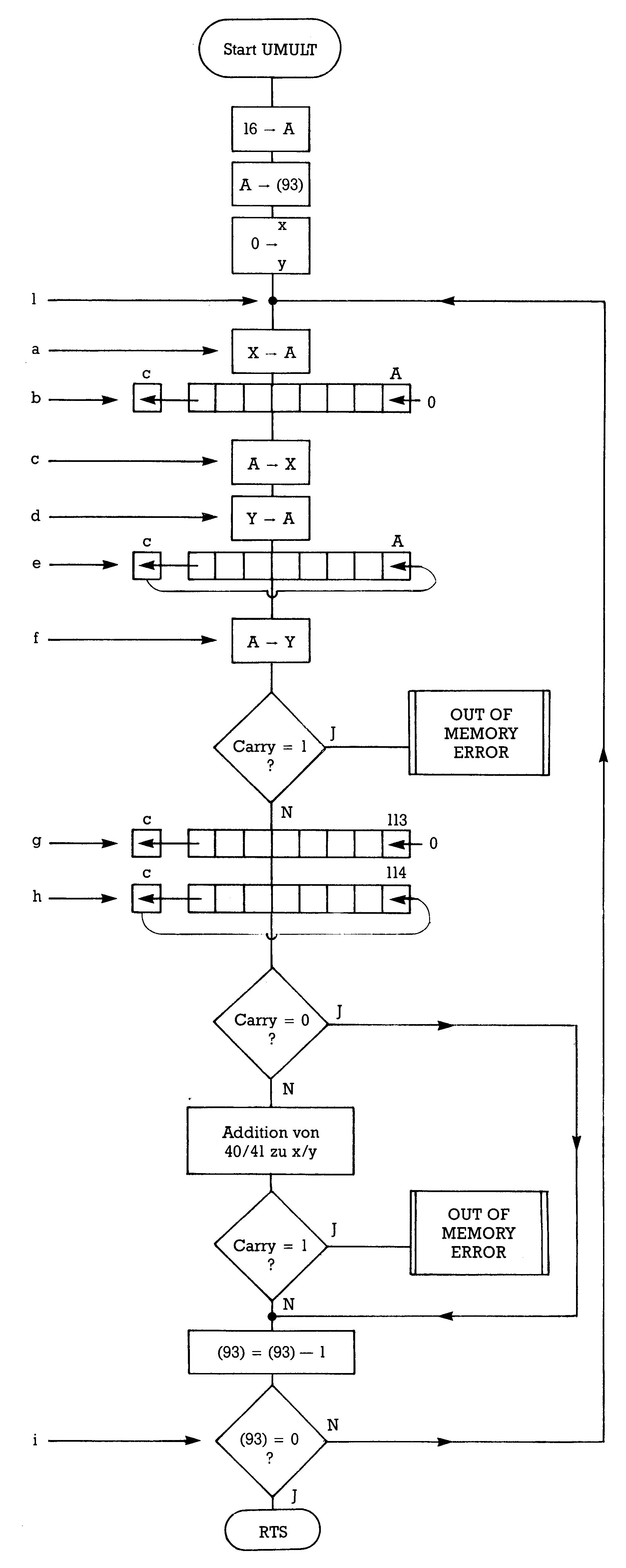
Faktor 1: 40/41
Faktor 2: 113/114
Ergebnis: X/Y
Das Ergebnis der Multiplikation befindet sich in LSB/MSB-Form in den X/Y-Registern. Programm und Flußdiagramm wollen wir an einem Beispiel nachspielen. Dazu sollen die beiden Zahlen 321 und 65 (binär 0000 0001 0100 0001 und 0100 0001) miteinander multipliziert werden, was bekanntlich 20865 (binär 0101 0001 1000 0001) ergibt. Was Ihnen im Bild 6 als undurchdringlicher Bit-Dschungel entgegenstrahlt, ist das schrittweise Verfolgen des Programms in Computerformat, also binär.
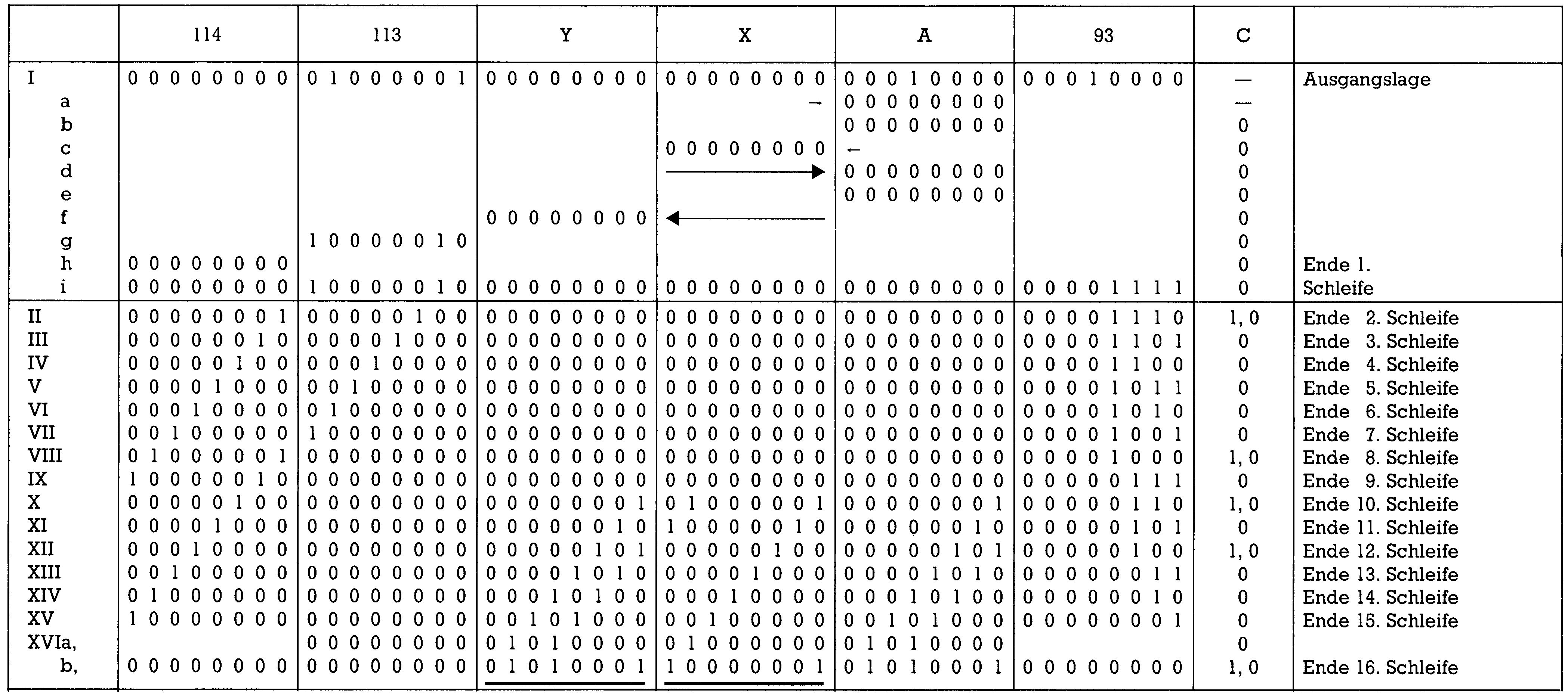
In Bild 6 sind die Speicheradressen alle dezimal angegeben. Dort finden Sie zunächst die Ausgangslage. In Speicherstelle 40/41 steht die ganze Operation über unverändert die Zahl 321. In 113/114 finden Sie (wegen des LSB/MSB-Formates umgedreht als 114/113) unseren Faktor 65. Akku und Speicherstelle 93 stehen auf 16, dem Bitzähler. In das X- und Y-Register wurde eine Null eingelesen. Im Flußdiagramm ist diese Situation mit einer 1 gekennzeichnet. Ganz unten im Diagramm sehen Sie, daß der Bitzähler 93 erniedrigt und danach geprüft wird, ob er schon gleich Null sei. Daraus folgt, daß die große Schleife 16mal durchlaufen wird. Den ersten Durchlauf (gekennzeichnet durch kleine Buchstaben) verfolgen wir im einzelnen.
- X-Register wird zur Bearbeitung in den Akku geschoben.
- Mittels ASL wird das Bit 7 in die Carry-Flagge geschoben, was einen Carry-Inhalt von 0 bewirkt.
- Der solchermaßen bearbeitete Akku-Inhalt (der sich hier nicht weiter verändert hat) geht wieder zurück ins X-Register.
- Nun ist das Y-Register zur Bearbeitung dran. Es gelangt in den Akku.
- Mittels ROL wandert nun das MSB des X-Registers aus dem Carry-Bit in die 0-Bit-Position des Akku
- und alles zusammen wieder ins Y-Register. Insgesamt wird dadurch die 16-Bit-Zahl im X/Y-Register um eine Stellenzahl erhöht, was der Vorbereitung zur Addition dient. (Erinnern Sie sich bitte: Die Kolonne der Einzelergebnisse wird ja addiert). Im Diagramm (ohne Buchstabenkennzeichnung) schließt sich hier noch eine Prüfung auf einen eventuellen Überlauf an, der dann mit einer Fehlermeldung beantwortet wird.
- Nun wird das MSB der Speicherstelle 113 nach links ins Carry geschoben. Das ist auch hier noch eine Null.
- Anschließend wandert dieser Carry-Inhalt als Bit 0 in Speicherstelle 114. Bit 7 von 114 landet dafür im Carry. Auch hier wird auf diese Weise die ganze 16-Bit-Zahl 113/114 um ein Bit nach links geschoben und im nächsten Schritt — im Flußdiagramm wieder ohne Buchstabe — geprüft, ob da eine 1 oder eine 0 ins Carry-Bit geshiftet wurde. Wenn lediglich eine Null auftrat — wie hier —, dann springt das Programm sofort zum Herabzählen des Bitzählers 93. Tritt aber eine 1 auf, dann addiert sich der Inhalt von 40/41 zu X/Y.
- Hier wird der Zustand der betroffenen Speicherstellen und Register nach dem ersten Schleifendurchlauf gezeigt.
Römisch II bis XVI zeigen nun jeweils den Zustand nach dem 2. bis 16. Durcharbeiten der großen Schleife. Wenn Sie verstehen möchten, was da passiert, sollten Sie versuchen, Bild 6 nur als Kontrolle zu verwenden und ansonsten mal selbst alle Schritte nachzuvollziehen.
16-Bit-Division
Beim umgekehrten Weg, nämlich der Teilung von zwei 16-Bit-Zahlen, haben wir nicht so viel Glück: Ich konnte keine derartige Routine im Interpreter entdecken. Nun gibt es aber fast in jedem Lehrbuch der Maschinensprache die Vorstellung eines solchen Programms, so daß man sich das schönste aussuchen kann. Das Prinzip ist auch da dasselbe, wie wir es von der normalen Division gewohnt sind: Der Divisor wird Schritt für Schritt vom Dividenden abgezogen. In der Literatur [1] fand ich eine sehr kurze Routine, die ich Ihnen leicht modifiziert als Programm 1 vorstellen will.
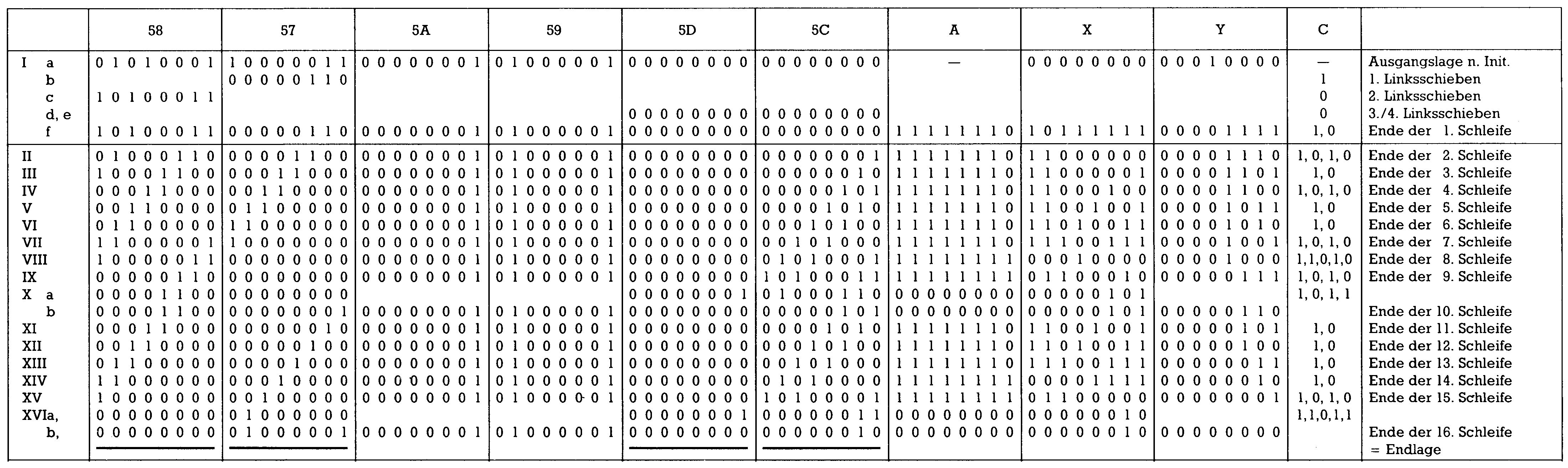
In Bild 7 ist ein Flußdiagramm dieser Routine gezeigt und in Bild 8 lacht Ihnen wieder das Bit-Gewirr entgegen, das Sie schon von der Multiplikation her kennen, hier aber für die Division.
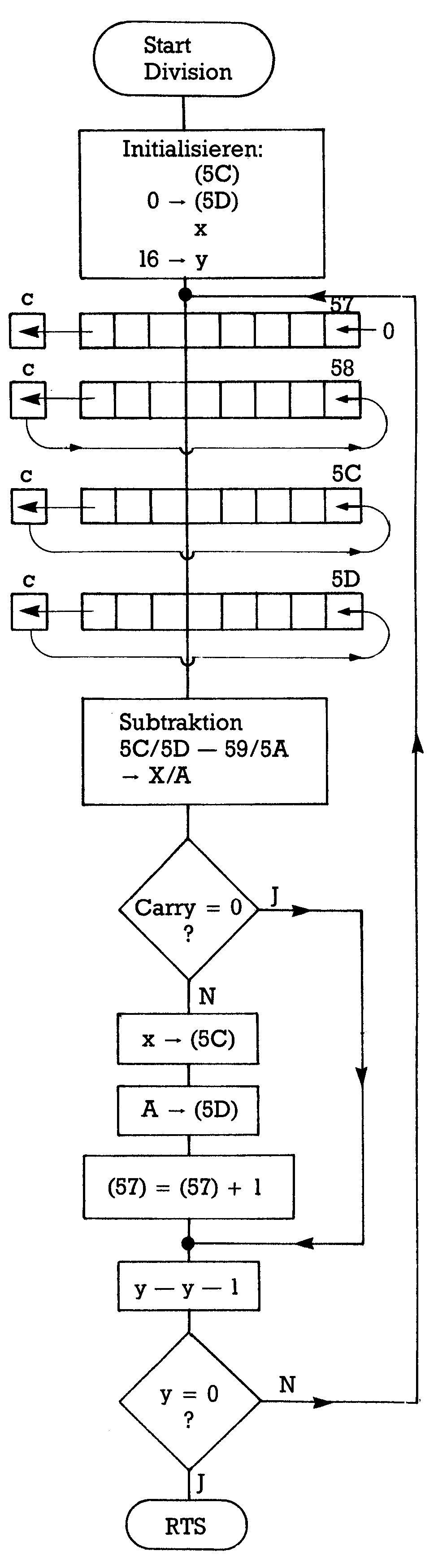
Damit Sie wissen, wo was hinein- oder herauskommt:
| A | : B | = C | + Rest |
| ↑ | ↑ | ↑ | ↑ |
| $57/$58 | $59/$5A | $57/58 | $5C/5D |
An dem folgenden Beispiel soll der Programmverlauf getestet werden: Wir teilen 20867 durch 321. Dabei kommt nach Adam Riese heraus: 65, Rest 2.
In folgender Weise wird in die Speicherzellen die Aufgabe eingespeist:
| 20867 | $57 | 1000 | 0011 | LSB |
| $58 | 0101 | 0001 | MSB | |
| 321 | $59 | 0100 | 0001 | LSB |
| $5A | 0000 | 0001 | MSB | |
| Als Ergebnis findet man dann: | ||||
| 65 | $57 | 0100 | 0001 | LSB |
| $58 | 0000 | 0000 | MSB | |
| Rest 2 | $5C | 0000 | 0010 | LSB |
| $5D | 0000 | 0000 | MSB | |
Als Bit-Zähler dient hier das Y-Register.
- b) Erstes Linksschieben des LSB mittels ASL. Dabei gelangt die 1 in das Carry-Bit.
- c) Hineinrotieren der 1 aus dem Carry in das MSB mittels ROL.
- d), e) Linksrotieren der 16-Bit-Zahl in $5C/5D, die jetzt noch 0 ist.
- f) Situation am Ende der ersten Schleife. Der Bitzähler ist um 1 reduziert.
Im folgenden wird dann jeweils die Situation am Ende der Schleife gezeigt. Beim Berechnen der Differenz muß jeweils darauf geachtet werden, daß die Subtraktion einer Zahl als Addition des Zweierkomplements ausgeführt wird. Das haben wir in den Folgen 3 und 4 der Serie kennengelernt. Allerdings muß an dieser Stelle nochmal gesagt werden, daß die 1, die zum Einerkomplement hinzuaddiert wird, um das Zweierkomplement zu erhalten, das gesetzte Carry-Bit ist. Nun dürfte es für Sie eigentlich keine Probleme mehr geben, was das Nachvollziehen der Divisionsroutine betrifft.
Damit dürfen wir getrost die 16-Bit-Arithmetik abschließen. Alle vier Grundrechnungsarten können Sie jetzt programmieren. Weitere Rechenarten, wie Potenzieren, das Ziehen von Wurzeln, Logarithmen etc. bedingen ohnehin, daß die Argumente oder Ergebnisse keine Integerzahlen sind. Hier werden wir dann mit Fließkommaarithmetik arbeiten und den dazu vorgesehenen Interpreterroutinen.
Das Programmprojekt wird fortgeführt
Im 6. Teil dieser Serie haben wir ein Projekt gestartet, das dort eine Kopfzeile rückholbar unter den oberen ROM-Bereich verschob. Unser Wissen ist seither gestiegen und damit auch unsere Ansprüche. Eine Kopfzeile reicht nicht mehr, jetzt soll es ein ganzer Hilfsbildschirm sein, den wir erst in aller Ruhe erstellen wollen, um ihn dann jederzeit abrufbar unter das Betriebssystem zu packen. Den Aufruf wollen wir wieder mit der USR-Funktion steuern. Diesmal soll aber so programmiert werden, daß der Hilfsbildschirm erhalten bleibt, man ihn also mehrfach einblenden kann. Über die Nützlichkeit einer solchen Routine braucht man sicherlich nicht viele Worte zu verlieren: Denken Sie da nur mal an Programme, die irgendwelche Tasten mit besonderen Funktionen belegen, für die Sie eine Gedächtnisstütze brauchen, oder …
Als Programm 2 ist ein kleines Demo-Programm abgedruckt, welches zuerst einen Bildschirm erstellt, dann die Routine »Verschieben« aufruft, den Bildschirm löscht und neu beschreibt und schließlich mit einem weiteren USR den alten Bildschirm einblendet (vorher Programm 3 und 4 laden).
Von nun an können Sie immer — auch im Direktmodus — durch ein USR-Kommando diesen Bildschirm abbilden. Zum Programm in der Folge 6 sind noch zwei Dinge zu bemerken, die hier geändert werden sollen. Erstens eine Frage: Ist Ihnen der Computer mal abgestürzt beim Aufruf des Programms? Die Wahrscheinlichkeit dafür ist ungefähr 1 : 60, wenn nämlich ein Interrupt stattfindet, während die Speicherstelle 1 geändert wird. Obwohl wir erst in den nächsten Folgen auf Interrupts eingehen werden, wollen wir die Wahrscheinlichkeit für so einen Absturz auf Null reduzieren. Eine andere Sache ist der Ort, an dem sich das Programm befand. Es hat sich nämlich herausgestellt, daß anscheinend die Nutzung dieses dort gewählten Speicherbereichs nicht ganz so problemlos ist. Bei einigen Anrufen wurde mir erzählt, daß zumindest der Anfang ab $02A7 bei bestimmten Konstellationen überschrieben wird. Deswegen packen wir unser Programm ganz unkonventionell nach $6000, von wo Sie es — das beherrschen Sie ja mit dem SMON inzwischen sicher — dorthin schieben können, wo es Ihnen gefällt. Allerdings müssen dann auch die USR-Adressen geändert werden. Aber auch das dürfte für Sie inzwischen kein Problem mehr sein.
Um diese immerhin schon 2000 Byte (1000 für den Bildschirm und nochmal 1000 für das Farb-RAM) zu verschieben, bedienen wir uns einer Interpreter-Routine, die seit Ausgabe 3/85 des 64’er auch beim Checksummer verwendet wird — der Blockverschiebe-Routine (Bild 9a).
| Name | BLTUC | ||||||
| Zweck | Verschieben von Speicherinhalten im Speicher | ||||||
| Adresse | $A3BF dez. 41919 | ||||||
| Vorbereitungen |
| ||||||
| Speicherstellen | $58-5B, $5F, $60, $22 | ||||||
| Register | Akku, X- und Y-Register | ||||||
| Stapelbedarf | keiner |
Wieder besteht unser Programm aus zwei Teilen. Im ersten wird der aktuelle Bildschirm nach oben geschoben. Dieser Teil speist lediglich zuerst die Adressen des Bildschirms und des Betriebssystem-ROM in die Abholspeicherstellen der danach aufgerufenen Routine BLTUC und wiederholt diesen Vorgang für die Bildschirmfarbspeicheradressen. Danach verstellen wir noch den USR-Vektor und kehren mit TRS ins Basic-Programm zurück (siehe Programm 3).
Komplexer ist der zweite Teil. Um nämlich die Informationen unter dem ROM lesen zu können, muß dieses ausgeschaltet werden. Leider läßt sich das Betriebssystem-ROM nur zusammen mit dem Basic-Interpreter ausschalten. $A3BF ist aber eine Interpreter-Routine! Da bleibt uns nichts anderes übrig, als diese Routine in unser Programm einzubauen, was uns die Gelegenheit gibt, sie uns mal etwas anzusehen. Als Bild 9 ist sie im Flußdiagramm abgebildet.
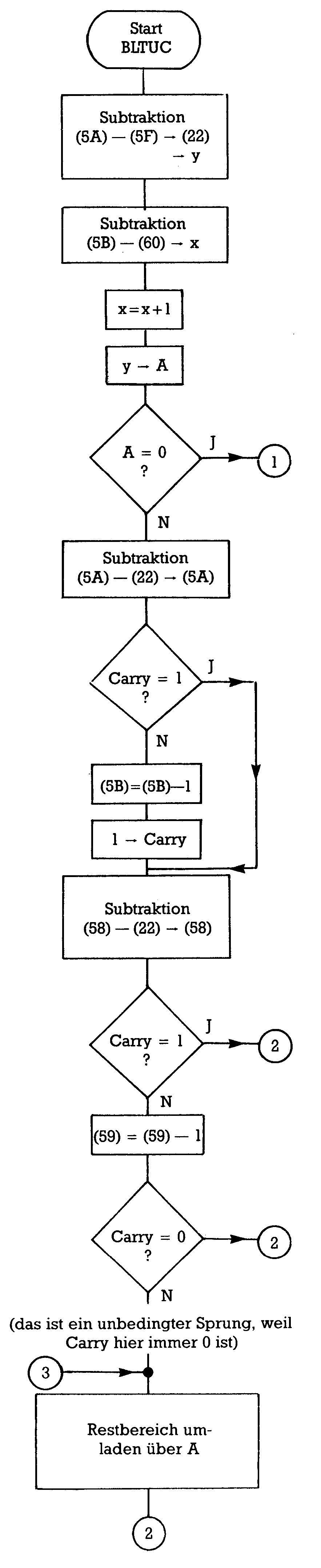
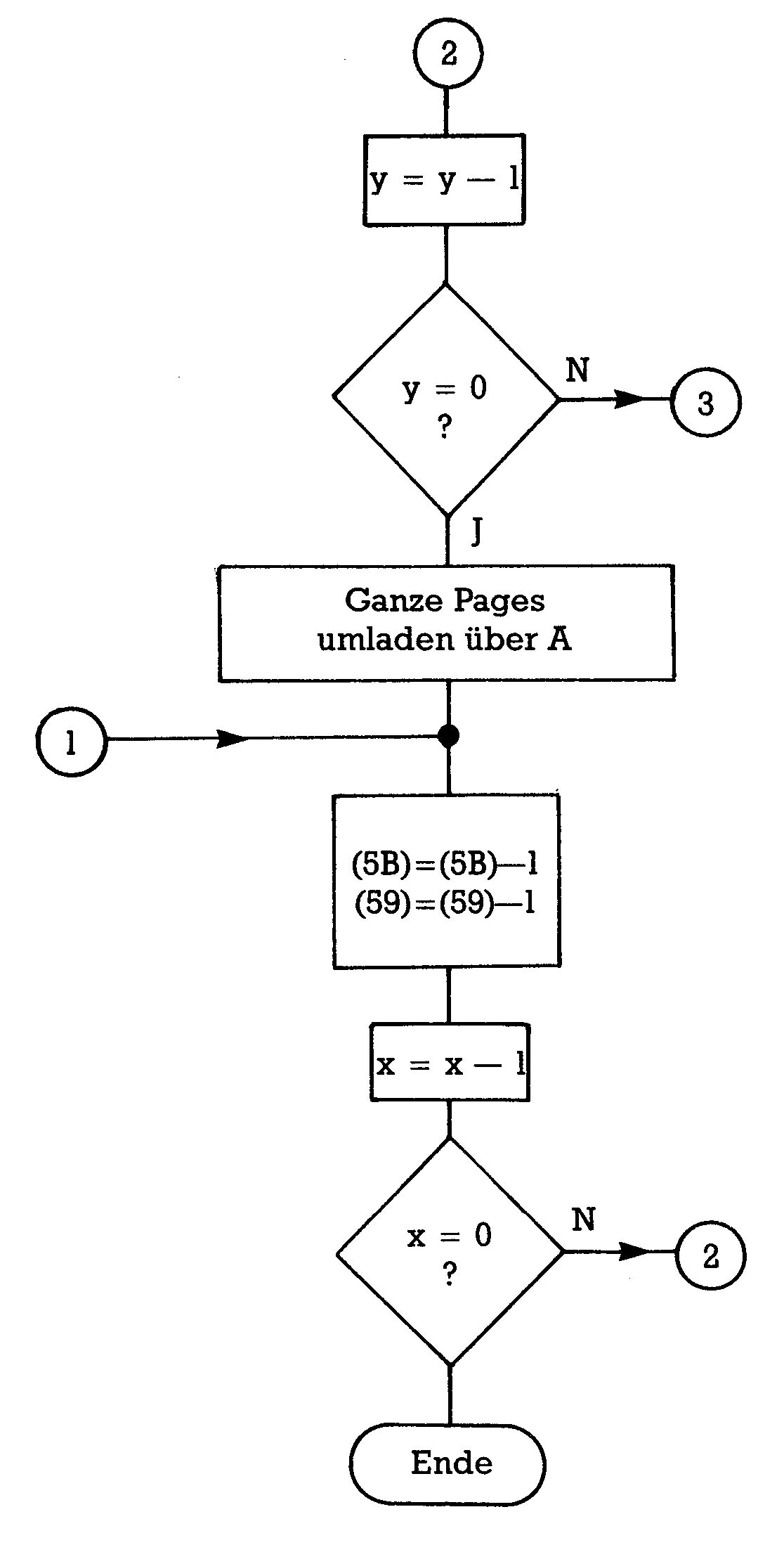
Programm 4 zeigt den zweiten Teil unseres Hilfsbildschirm-Programms.
Von $6040 an, wohin wir am Ende des ersten Teils den USR-Vektor gerichtet haben, wird zunächst wieder Quell- und Zielbereich in den Abholspeicherstellen spezifiziert und jeweils danach zuerst für den Bildschirm, dann für das Farb-RAM, das übernommene Unterprogramm angesprungen. Ab $6077 liegt dann das modifizierte Unterprogramm. Die Befehle SEI und CLI gehören zu den wenigen, die Sie erst noch kennenlernen. Sie sind es, die die Absturzwahrscheinlichkeit auf Null bringen. Jedenfalls wird zuerst das ROM aus und dafür RAM eingeschaltet. Ab $607F bis $60B9 befindet sich die Interpreter-Routine BLTUC. Darin wird zunächst die Länge des zu verschiebenden Bereichs berechnet, dann festgestellt, ob nur ganze Pages (Seiten) oder auch ein Restbereich verschoben werden soll. Falls ein solcher Restbereich vorhanden ist, wird auch seine Länge berechnet und zuerst dieser verschoben. Daran schließt sich das Verschieben der ganzen Pages an. Das X- und das Y-Register dienen dabei als Zähler.
Ab $60BB schließt sich wieder unsere eigene Routine an, in der wir die ROMs wieder einschalten. Auf diese Weise lassen sich noch mehrere Hilfsbildschirme unter ROM-Bereiche packen. Vielleicht überlegen Sie sich mal dazu einen Weg?
Die ROM-Bereiche als Datenquelle
Die ROM-Bereiche enthalten nicht nur ausgeklügelte Maschinenprogramme, sondern auch eine Menge Daten. Sollten Sie mal in die Verlegenheit kommen, beispielsweise die Zahl Pi im MFLPT-Format verwenden zu müssen, dann erfordert das einen ganz schönen Aufwand an Rechen- und Programmarbeit, oder Sie möchten bestimmte Texte wie beispielsweise eine Fehlermeldung verfügbar halten …. und so weiter. Viele von diesen Daten sind schon in der Firmware enthalten und wir werden im folgenden festhalten, wo sie sich befinden und welches Format man vorfindet. Sehen wir uns zunächst Zahlen an (Tabelle 1). Es existieren noch weitere Zahlentabellen in den ROM-Bereichen, die aber selten von Interesse sind. Ebenso wie Zahlen, findet man auch Texte im ROM als ASCII-Werte abgelegt (Tabelle 2):
| Startadresse | Format | Zahl |
| $AEA8 | MFLPT | Pi |
| $B1A5 | MFLPT | -32768 |
| $B9BC | MFLPT | 1 |
| $B9C1 | 1-Byte-Integer | 3 |
| $B9C2 | MFLPT | 0.434255942 |
| $B9C7 | MFLPT | 0.576584541 |
| $B9CC | MFLPT | 0.961800759 |
| $B9D1 | MFLPT | 2.88539007 |
| $B9D6 | MFLPT | 0.707106781 = SQR(1/2) |
| $B9DB | MFLPT | 1.41421356 = SQR(2) |
| $B9E0 | MFLPT | -0.5 |
| $B9E5 | MFLPT | 0.693147181 = ln2 |
| $BAF9 | MFLPT | 10 |
| $BDB3 | MFLPT | 99 999 999.9 |
| $BDB8 | MFLPT | 999 999 999 |
| $BDBD | MFLPT | 1 000 000 000 |
| $BF11 | MFLPT | 0.5 |
| $BF16 | 4-Byte-Integer | -100 000 000 |
| $BF1A | — " — | 10 000 000 |
| $BF1E | — " — | -1 000 000 |
| $BF22 | — " — | 100 000 |
| $BF26 | — " — | -10 000 |
| $BF2A | — " — | 1 000 |
| $BF2E | — " — | -100 |
| $BF32 | — " — | 10 |
| $BF36 | — " — | -1 |
| $BF3A | — " — | -2 160 000 |
| $BF3E | — " — | 216 000 |
| $BF42 | — " — | -36 000 |
| $BF46 | — " — | 3 600 |
| $BF4A | — " — | -600 |
| $BF4E | — " — | 60 |
| $BFBF | MFLPT | 1.44269504 = 1/ln2 |
| $BFC4 | 1-Byte-Integer | 7 |
| $BFC5 | MFLPT | 2.14987637E-05 |
| $BFCA | MFLPT | 1.43523140E-04 |
| $BFCF | MFLPT | 1.34226348E-03 |
| $BFD4 | MFLPT | 9.61401701E-03 |
| $BFD9 | MFLPT | 0.0555051269 |
| $BFDE | MFLPT | 0.240226385 |
| $BFE3 | MFLPT | 0.693147186 = ln2 |
| $BFE8 | MFLPT | 1 |
| $E08D | MFLPT | 11 879 546 |
| $E092 | MFLPT | 3.92767774E-08 |
| $E2E0 | MFLPT | 1.57079633 = Pi/2 |
| $E2E5 | MFLPT | 6.28318531 = 2*Pi |
| $E2EA | MFLPT | 0.25 |
| $E2EF | 1-Byte-Integer | 5 |
| $E2F0 | MFLPT | -14.3813907 |
| $E2F5 | MFLPT | 42.0077971 |
| $E2FA | MFLPT | -76.7041703 |
| $E2FF | MFLPT | 81.6052237 |
| $E304 | MFLPT | -41.3417021 |
| $E309 | MFLPT | 6.28318531 = 2*Pi |
| $E33E | 1-Byte-Integer | 11 |
| $E33F | MFLPT | -6.8473912E-04 |
| $E344 | MFLPT | 4.85094216E-03 |
| $E349 | MFLPT | -0.0161117018 |
| $E34E | MFLPT | 0.034209638 |
| $E353 | MFLPT | -0.0542791328 |
| $E358 | MFLPT | 0.0724571965 |
| $E35D | MFLPT | -0.0898023954 |
| $E362 | MFLPT | 0.110932413 |
| $E367 | MFLPT | -0.142839808 |
| $E36C | MFLPT | 0.19999912 |
| $E371 | MFLPT | -0.333333316 |
| $E376 | MFLPT | 1 |
| $E3BA | MFLPT | 0.811635157 |
| $E8DA - $E8E9 | 1-Byte-Integers | Tabelle der Farbcodes |
| $EB81 - $EBC1 | — " — | Tastaturdecodierung: Einzelne Tasten |
| $EBC2 - $EC02 | 1-Byte-Integers | Tasten mit Shift |
| $EC03 - $EC43 | 1-Byte-Integers | Tasten mit Commodore-Taste |
| $EC78 - $ECB8 | 1-Byte-Integers | Tasten mit Control-Taste |
| $ECB9 - $ECE5 | 1-Byte-Integers | VIC-II-Chip-Registerwerte |
| $ECF0 - $ED08 | 1-Byte-Integers | Tabelle der LSBs der Bildschirm-Anfangsadressen |
| $A004 | CBMBASIC |
| $A09E - $A19D | Texte der Basic-Befehlsworte (im letzten Byte ist jeweils Bit 7 gesetzt) |
| $A19E - $A327 | Texte der Basic-Fehler- und System-Meldungen. (Im letzten Byte ist jeweils Bit 7 gesetzt) |
| $A364 - $A38A | Weitere System-Meldungen: OK, ERROR, IN, READY, BREAK. (Das letzte Bvte ist jeweils 0) |
| $ACFC - $AD1D | Fehlermeldungstexte für INPUT: ?EXTRA IGNORED, ?REDO FROM START. (Das letzte Byte ist jeweils 0) |
| $E460 | BASIC BYTES FREE |
| $E473 | **** COMMODORE 64 BASIC V2 **** 64K-RAM-System |
| $ECE6 | LOAD (Return) RUN (Return) |
| $F0BD - $F12B | Texte für Ein- und Ausgabe-Onerationen |
| $FD10 | CBM80 |
Sollten Sie mal in die Verlegenheit kommen, solche Texte ausgeben zu wollen, dann legen Sie sie nicht nochmal in einer eigenen Texttabelle ab, sondern schöpfen Sie aus dem Fundus, den wir im ROM-Bereich fix und fertig haben.
Diese Folge soll nicht abgeschlossen werden, ohne eine Korrektur. Auf einen Fehler, dem ich aufgesessen bin (in der Literatur befinde ich mich aber in guter Gesellschaft, andere sind auch davon betroffen), haben mich zwei aufmerksame Leser hingewiesen. Es dreht sich um die Flaggensetzung bei Compare-Befehlen. Die N-Flagge ist nämlich nicht nur vom Ergebnis des Vergleichs, sondern auch noch von den aktuellen Akku- beziehungsweise Registerinhalten bestimmt.
Bild 1 in der 5. Folge muß deshalb korrigiert werden:
- (A,X,Y) größer als die Daten: N kann 0 oder 1 sein
- (A,X,Y) = Daten N = 0
- (A,X,Y) kleiner als die Daten: N kann 0 oder 1 sein.
Das stammt aus dem offziellen MOS-Technology-Handbuch und entspricht somit hoffentlich der Wahrheit [2]. Das bedeutet, daß man bei den Abfragen durch Branch-Befehle nach den Vergleichsbefehlen etwas vorsichtig sein sollte, was die N-Flagge angeht.
Zum Schluß noch, wie üblich, die Tabelle 3 mit den neuen Assembler-Befehlen.
(Heimo Ponnath/gk)- [1] »Computerspiele und Wissenswertes Commodore 64«, Haar bei München: Markt & Technik Verlag, 1984. Das ist die von P. Lücke besorgte Übersetzung des amerikanischen Buches »More on the sixtyfour« und ist jedem Assembler-Programmierer warm zu empfehlen.
- [2] »MOS Microcomputers Programmier-Handbuch«, Frankfurt: Commodore MOS Technology
| Befehlswort | Adressierung | Bytezahl | Code | Taktzyklen | Beinflussung von Flaggen | |
| Hex | Dez | |||||
| LSR | »Akkumulator« | 1 | 1A | 26 | 2 | N,Z,C |
| absolut | 3 | 4E | 78 | 6 | N,Z,C | |
| 0-page-absolut | 2 | 46 | 70 | 5 | N,Z,C | |
| absolut-X-indiz. | 3 | 5E | 94 | 7 | N,Z,C | |
| 0-page-X-indiz. | 2 | 56 | 86 | 6 | N,Z,C | |
| ROL | »Akkumulator« | 1 | 2A | 42 | 2 | N,Z,C |
| absolut | 3 | 2E | 46 | 6 | N,Z,C | |
| 0-page-absolut | 2 | 26 | 38 | 5 | N,Z,C | |
| absolut-X-indiz. | 3 | 3E | 62 | 7 | N,Z,C | |
| 0-page-X-indiz. | 2 | 36 | 54 | 6 | N,Z,C | |
| ROR | »Akkumulator« | 1 | 6A | 106 | 2 | N,Z,C |
| absolut | 3 | 6E | 110 | 6 | N,Z,C | |
| 0-page-absolut | 2 | 66 | 102 | 5 | N,Z,C | |
| absolut-X-indiz. | 3 | 7E | 126 | 7 | N,Z,C | |
| 0-page-X-indiz. | 2 | 76 | 118 | 6 | N,Z,C | |
. ,5000 a2 00 ldx #00 ,5002 86 5c stx 5c ,5004 86 5d stx 5d ,5006 a0 10 ldy #10 ,5008 06 57 asl 57 ,500a 26 58 rol 58 ,500c 26 5c rol 5c ,500e 26 5d rol 5d ,5010 38 sec ,5011 a5 5c lda 5c ,5013 e5 59 sbc 59 ,5015 aa tax ,5016 a5 5d lda 5d ,5018 e5 5a sbc 5a ,501a 90 06 bcc 5022 ,501c 86 5c stx 5c ,501e 85 5d sta 5d ,5020 e6 57 inc 57 ,5022 88 dey ,5023 d0 e3 bne 5008 ,5025 60 rts ----------------------- .?
1 rem ********************************* 2 rem * * 3 rem * programm 2 * 4 rem * * 5 rem * erstellen und aufruf eines * 6 rem * hilfsbildschirmes * 7 rem * * 8 rem * heimo ponnath hamburg 1985 * 9 rem ********************************* 10 printchr$(147):poke785,0:poke786,96:goto30 15 rem -------- up cursor setzen ------ 20 poke211,sp:poke214,z:sys58640:return 25 rem- erstellen des hilfsbildschirmes- 30 z=1:sp=1:gosub20:print"**************************************" 40 z=21:sp=1:gosub20:print"**************************************" 50 z=10:sp=7:gosub20:print"test fuer die verschiebung" 55 rem ---- aufruf zum verschieben ---- 60 a=usr(dummy) 65 rem ---bildschirm neu beschreiben--- 70 geta$:ifa$=""then70 80 printchr$(147):z=2:sp=2:gosub20:print"jetzt sollte der alte bildschirm" 90 z=4:sp=2:gosub20:print"unter das kernal-rom geschoben sein" 100 print:print:print" -- jeder usr-aufruf holt den --" 110 print" -- hilfsbildschirm wieder . --" 120 print" -- auch im direkt-modus --" 130 print:print:print" probieren sie mal: a=usr(1) [return]" 140 z=19:sp=0:gosub20:end
. ,6000 a9 00 lda #00 ,6002 85 5f sta 5f ,6004 a9 04 lda #04 ,6006 85 60 sta 60 ,6008 a9 e8 lda #e8 ,600a 85 5a sta 5a ,600c 85 58 sta 58 ,600e a9 07 lda #07 ,6010 85 5b sta 5b ,6012 a9 e3 lda #e3 ,6014 85 59 sta 59 ,6016 20 bf a3 jsr a3bf ,6019 a9 00 lda #00 ,601b 85 5f sta 5f ,601d a9 d8 lda #d8 ,601f 85 60 sta 60 ,6021 a9 e8 lda #e8 ,6023 85 5a sta 5a ,6025 a9 db lda #db ,6027 85 5b sta 5b ,6029 a9 d1 lda #d1 ,602b 85 58 sta 58 ,602d a9 e7 lda #e7 ,602f 85 59 sta 59 ,6031 20 bf a3 jsr a3bf ,6034 a9 40 lda #40 ,6036 8d 11 03 sta 0311 ,6039 a9 60 lda #60 ,603b 8d 12 03 sta 0312 ,603e 60 rts ---------------------- .?
. ,603f ea nop ,6040 a9 00 lda #00 ,6042 85 5f sta 5f ,6044 a9 e0 lda #e0 ,6046 85 60 sta 60 ,6048 a9 e8 lda #e8 ,604a 85 5a sta 5a ,604c 85 58 sta 58 ,604e a9 e3 lda #e3 ,6050 85 5b sta 5b ,6052 a9 07 lda #07 ,6054 85 59 sta 59 ,6056 20 77 60 jsr 6077 ,6059 a9 e9 lda #e9 ,605b 85 5f sta 5f ,605d a9 e3 lda #e3 ,605f 85 60 sta 60 ,6061 a9 d1 lda #d1 ,6063 85 5a sta 5a ,6065 a9 e7 lda #e7 ,6067 85 5b sta 5b ,6069 a9 e8 lda #e8 ,606b 85 58 sta 58 ,606d a9 db lda #db ,606f 85 59 sta 59 ,6071 20 77 60 jsr 6077 ,6074 60 rts ---------------------------- ,6075 ea nop ,6076 ea nop ,6077 78 sei ,6078 a5 01 lda 01 ,607a 48 pha ,607b a9 35 lda #35 ,607d 85 01 sta 01 ,607f 38 sec ,6080 a5 5a lda 5a ,6082 e5 5f sbc 5f ,6084 85 22 sta 22 ,6086 a8 tay ,6087 a5 5b lda 5b ,6089 e5 60 sbc 60 ,608b aa tax ,608c e8 inx ,608d 98 tya ,608e f0 23 beq 60b3 ,6090 a5 5a lda 5a ,6092 38 sec ,6093 e5 22 sbc 22 ,6095 85 5a sta 5a ,6097 b0 03 bcs 609c ,6099 c6 5b dec 5b ,609b 38 sec ,609c a5 58 lda 58 ,609e e5 22 sbc 22 ,60a0 85 58 sta 58 ,60a2 b0 08 bcs 60ac ,60a4 c6 59 dec 59 ,60a6 90 04 bcc 60ac ,60a8 b1 5a lda (5a),y ,60aa 91 58 sta (58),y ,60ac 88 dey ,60ad d0 f9 bne 60a8 ,60af b1 5a lda (5a),y ,60b1 91 58 sta (58),y ,60b3 c6 5b dec 5b ,60b5 c6 59 dec 59 ,60b7 ca dex ,60b8 d0 f2 bne 60ac ,60ba 68 pla ,60bb 85 01 sta 01 ,60bd 58 cli ,60be 60 rts ---------------------------- .?
