Reise durch die Wunderwelt der Grafik - Teil 7

In dieser letzten Folge des Grafikkursus wird auf das Hinterschneidungsproblem eingegangen. Außerdem wird eine Lösung für die gleichzeitige Darstellung von hochauflösender Grafik, Text und Mehrfarb-Bit-Map auf einem Bildschirm gezeigt.

Dies ist die letzte Folge unseres Grafikkurses. In der nächsten Ausgabe wird noch ein Maschinenprogramm gezeigt, das die Grafik unterstützt. Das Dornröschen (unsere hochauflösende Grafik) wird dann völlig erwachen und ihre Behäbigkeit wird sich verlieren.

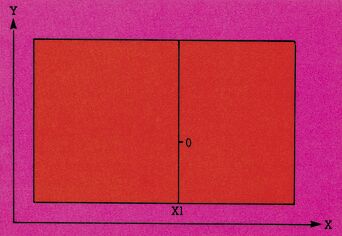
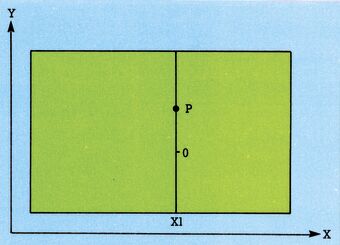
Es stellte sich die Frage, wie man es wohl erreichen könnte, daß nur sichtbare Teile einer Raumfläche gezeichnet werden. H.W. Franke hat in einem Artikel über Computergrafik geschrieben: »Bis heute kann man das Problem noch nicht als völlig abgeschlossen ansehen«. Damit meinte er das Hinterschneidungsproblem. Zumindest für unsere Aufgabenstellung und den C 64 kann man es lösen, wenn man folgendem Gedankengang verfolgt. Stellen Sie sich doch mal den Bildschirm des C 64 in 320 senkrechte Linien unterteilt vor, für jeden möglichen X-Wert also eine Senkrechte. Nun nehmen wir mal eine davon (bei X = X1) und ordnen ihr in unserem Koordinatensystem willkürlich einen Y-Wert 0 zu (Bild 1). In der Doppelschleife (siehe 3D-Programm in der letzten Folge) wird nun irgendwann X = XI sein und dann der dazugehörige Y-Wert berechnet. Dieser soll zum Beispiel gleich 1 sein. Der Punkt wird gesetzt, und die Schleife läuft weiter (Bild 2).

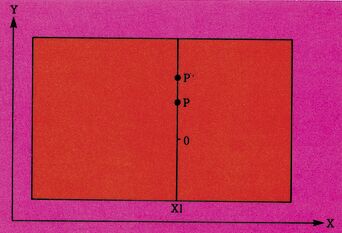
Wenn alle X-Werte durchlaufen wurden, erhöht sich der Z-Wert in der äußeren Schleife und von neuem wird für XI ein Y-Wert berechnet. Nehmen wir an, der läge bei 1,5. Auch dieser Punkt wird gesetzt und die Schleife geht weiter (Bild 3).

Wenn nun beim nächsten Schleifendurchlauf XI erreicht ist, wird es spannend. Es gibt nun drei Möglichkeiten (Bild 4).

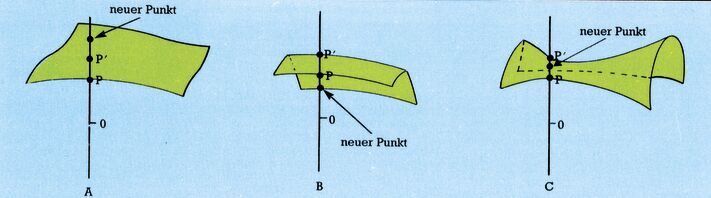
In Fall A liegt der neue Punkt oberhalb von P', ist sichtbar und wird gezeichnet. Im Fall B liegt er unterhalb von P, ist ebenfalls sichtbar und wird gezeichnet. Im Fall C aber liegt er zwischen P und P', er ist nicht sichtbar, weil er auf einem uns abgewandten Hang der Raumfläche liegt und wird daher nicht gezeichnet. Sie sehen also, daß wir uns lediglich immer auf jeder dieser Senkrechten den bisher größten und den bisher kleinsten Wert von Y merken müssen. Bei jedem neuen Y-Wert können wir feststellen, ob er innerhalb des damit aufgespannten Bereiches liegt (dann wird er nicht gezeichnet) oder außerhalb (dann wird er gezeichnet und dieser Wert als der größte oder kleinste bisherige gemerkt). Damit ist für uns das Problem gelöst! Wir richten ein zweidimensionales Feld ein: G (319, 2), wo für jede der 320 Senkrechten drei Werte gespeichert werden können:
G(X,0) als bisher höchster Y-Wert,
G(X,1) als bisher kleinster Y-Wert,
G(X,2) als Kennmarke, ob für diesen X-Wert schon ein Y-Wert aufgetaucht ist (in dem Fall ist G(X,2)>0) oder noch nicht (dann ist G(X,2) = 0). Durch das RUN-Kommando sind alle Variablen gleich 0, also auch G(X,2). Genau besehen benötigen wir diese Kennmarke, ob auf der Senkrechten durch X schon ein Punkt gesetzt wurde, nicht unbedingt in unserem Programm. Es ist so gestaltet, daß beim X-Durchlauf keine Lücken gelassen werden. Sinnvoll ist es trotzdem, sie einzurichten, denn durch die 45° -Verschiebung erhöht sich ja der maximale X-Wert ständig und außerdem könnte man sich ja mal überlegen, ob man den X-Durchlauf mit Lücken macht. In der letzten Folge hatten wir im Flußdiagramm unsere Doppelschleife entwickelt. Dabei war ein Teil »Zeichnen des Punktes X,Y«. Diesen Teil ersetzen wir durch den in Bild 5.

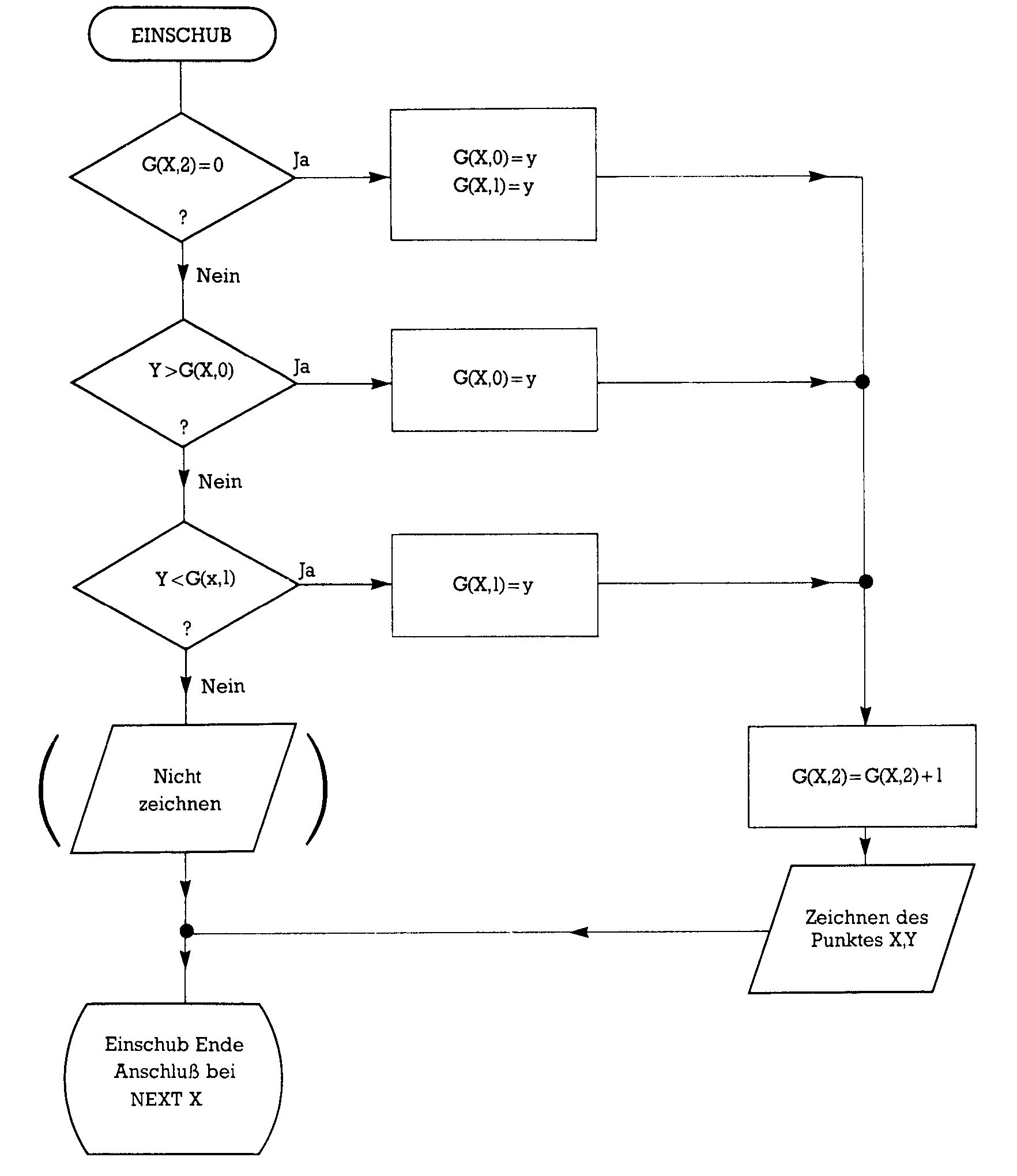
Jetzt sehen wir uns das als Programmteil an. Also Computer anschalten, Laden des 3D-Programmes aus der letzten Folge sowie der Grafik-Unterprogramme aus der vierten Folge (entweder — falls Sie das haben — durch MERGEn oder als kombiniertes Programm aus der Arbeit in der letzten Folge). Zeile 230 des 3D-Programmes enthält als letzten Befehl GOSUB 50040, den Aufruf zum »Punkt zeichnen«. Den löschen wir jetzt und fügen die folgenden Zeilen ein:
232 IF G(X,2) = 0THEN G(X,0) = Y:G(X,1)=Y:GOTO 238
234 IF Y>G(X,0) THEN G(X,0) = Y:GOTO 238
236 IF Y<G(X,1) THEN G(X,1) = Y:GOTO 238
237 GOTO 240
238 G(X,2) = G(X,2) + 1:GOSUB 50040
Außerdem muß natürlich zu Beginn dieses Feld noch dimensioniert werden: 147 DIM G (319,2)
Mit der Beispielfunktion Y=COS(Z) *SIN(X) und den Eingaben:XU = -1, XO = 10, YU=-2, YO = 5, ZU = -.1, ZO = 7, Schrittweite = 8,XA = 0,XE = 6, ZA = .1, ZE = 7 sieht man den Effekt jetzt ganz deutlich. Das einzige — außer der Geschwindigkeit (und naja - vielleicht noch ein paar Kleinigkeiten) — was unsere 3D-Grafik jetzt von professionellen Systemen unterscheidet, ist die Möglichkeit der Netzgrafik (Bild 6).

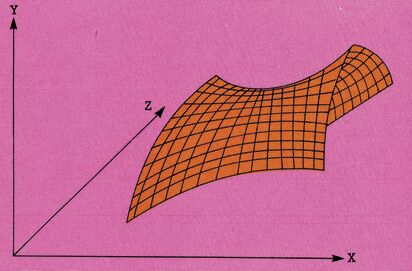
Dieses Thema soll nicht ausführlich behandelt werden, sondern wir werden nur zwei Wege zur Netzgrafik anschauen:

Weg 1:

Wir machen die Schrittweite in Z-Richtung sehr klein (so wie die in X-Richtung), setzen aber nicht jeden Punkt, sondern zum Beispiel in folgender Anordnung:

1. 1. Z-Wert: Jeder Punkt der X-Schleife wird gesetzt, dann
2. 2. bis 7. Z-Wert: Nur jeder 8.Punkt der X-Schleife wird gesetzt, dann
3. wieder weiter wie beim 1. Z-Wert und so weiter.

Stark vergrößert hätten wir dann etwa Verhältnisse wie in Bild 7.

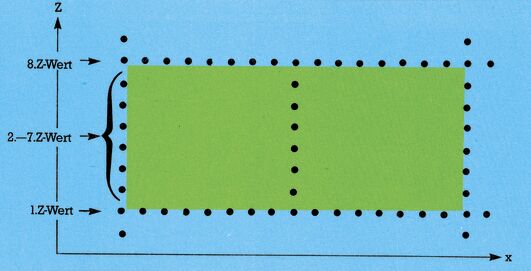
Diese Lösung ist programmtechnisch einfacher als Weg 2 und ganz gut an unser bisheriges 3D-Programm anzuhängen. Nun aber noch zu

Weg 2:

Man läßt außer der Z-X-Doppelschleife zur Berechnung von Y auch noch eine X-Z-Doppelschleife laufen. Wenn Sie das ausprobieren, gibt es allerdings wieder Schwierigkeiten mit den nicht sichtbaren Linien, denn unser Verfahren zur Lösung des Hinterschneidungsproblems läßt nichts mehr zeichnen, was innerhalb von G(X,0) bis G(X,1) liegt!

Anscheinend hat man bisher noch keine Möglichkeit Erklärungen auf das Grafikbild zu schreiben. Wenn wir im Hochauflösungsmodus zum Beispiel das Programm durch <RUN/STOP> anhalten, dann tauchen alle Meldungen als farbige Quadrate auf dem Bildschirm auf. Der Inhalt des Bildschirmspeichers dient ja jetzt als Farbinformation. Was der Computer mit dieser Farbkombination dann jeweils auf dem Bildschirm zeigen soll, holt er sich aus der Bit-Map. Man kann natürlich ohne weiteres die wichtigsten Zeichen aus Punkten, Linien und Ellipsenbögen zusammenbauen unter Verwendung unserer Grafik-Unterprogramme. Das wäre sozusagen der »harte« Weg. Aber wozu haben wir im Speicher schon die fertigen Zeichenmuster liegen! Wir müßten nur auf sinnvolle Weise an sie herankommen. Prinzipiell gibt es zwei »weiche« Wege:

a) Herbert Kunz hat den einen davon in der Zeitschrift Computer persönlich, Ausgabe 2 (1984), Seite 78 vorgestellt. Er kopiert zunächst den Zeichensatz in einen RAM-Bereich, schaltet dann — wie gewohnt — in den Hochauflösungsmodus (bei ihm liegt der Bildschirm bei 1024 und die Bit-Map richtet er bei 8192 ein) und druckt den Text auf den Bildschirm, wo dieser erst mal in farbigen Quadraten auftaucht. Nun sieht er mittels PEEK nach, welches Zeichen an der Bildschirmstelle steht (wo jetzt natürlich nur ein farbiges Quadrat zu sehen ist). Was Herbert Kunz dadurch erhält, ist die Kennzahl (der Bildschirmcode, zum Beispiel für ein A eine 1), die uns sagt, an welcher Stelle der Zeichentabelle das gefragte Zeichen steht. Dabei ist allerdings zu bedenken, daß es auch eine nullte Stelle gibt. Jedes Zeichen besteht aus 8 Bytes und deshalb multipliziert er die Kennzahl mit 8 und addiert sie zur Startadresse des RAM-Bereiches hinzu, in den er das Zeichen-ROM kopiert hat. Von da an überträgt er Byte für Byte das Zeichen in die entsprechende Stelle der Bit-Map (die er aus Zeilen und Spaltenangabe berechnet). So wird es dann sichtbar.

Das macht er Zeichen für Zeichen bis der gesamte — in einem String definierte — Text in der Bit-Map und damit für uns lesbar auf dem Bildschirm steht. Dieses Prinzip können wir in unsere Programme übernehmen. Dazu sind nur wenige Änderungen nötig. Zunächst schließen wir den neuen Zeichen-Speicher im RAM direkt an unsere Bit-Map an: ab 32768. Das Maschinenprogramm von Herbert Kunz verändern wir deshalb etwas und legen es nicht in den Kassettenpuffer, sondern von dez. 673 bis 715. Wie im Programm von Herbert Kunz brauchen wir dann nur noch die Angaben, in welcher Zeile und Spalte welcher Text geschrieben werden soll.

Zunächst einmal wird das Maschinenprogramm eingelesen und ausgeführt. In das 2D- und in das 3D-Programm fügen wir ein:
500 FOR I = 673 TO 715: READ A:POKE I, A:NEXTI:SYS 673: RETURN
510 DATA 120, 169, 49, 133, 1, 169, 0, 133, 98, 133,100, 169, 208, 133, 99, 169, 128, 133
520 DATA 101, 162, 16, 160, 0, 177, 98, 145, 100, 200, 208, 249, 230, 99, 230, 101, 202, 208
530 DATA 242, 169, 55, 133, 1, 88, 96

In Zeile 5 hängen wir an die beiden POKE-Kommandos noch an :GOSUB 500

In Zeile 120 definieren wir einen String, der einen senkrechten Tabulator ermöglicht:
120 CP$ = CHR$ (19):FOR I = 1 TO 24:CP$ = CP$ + CHR$ (17):NEXT I
Dann definieren wir den zu druckenden String und Zeile und Spalte des Druckortes:
122 TE$ = "Y” + F$:ZE = 0:SP = 0

Jetzt müssen wir nur noch dafür sorgen, daß nach dem Zeichnen der Kurve oder Raumfläche der Text gedruckt wird. Dazu gleichen wir zunächst mal das 2D- an das 3D-Programm an. In den Zeilen 200, 210, 220 des 2D-Programmes ändern wir die Zeilennummern zu 300, 310, 320 (dann muß natürlich in Zeile 300 die Anweisung THEN 200 zu THEN 300 umgeschrieben werden und die alten Zeilen 200 bis 220 gelöscht werden). Im 2D-Programm hört das Zeichnen in Zeile 195, im 3D-Programm in Zeile 250 auf. Deswegen legen wir den Druckvorgang ab Zeile 260:
260 PRINT LEFT$ (CP$,ZE+1)TAB (SP)TE$;
262 AN = 23552 + ZE * 40 + SP:GS = 24576 + ZE * 320 + SP * 8
264 FOR I = AN TO AN + LEN (TE$)-1
266 L = PEEK (I) :Z = 32768 + 8 * L:POKEI, 16*F1 + F2
268 FOR J = 0 TO 7:POKE GS+J, PEEK (Z+J):NEXTJ
270 GS = GS + 8:NEXTI

Wenn Sie das Programm (2D- oder 3D-Programm) jetzt starten, bekommen Sie als Kopf des Hochauflösungsbildschirmes noch die gezeichnete Funktion als Gleichung gedruckt. Sie können sich leicht aus diesen Angaben ein Programm schreiben, in dem die Zeilen 260 bis 270 ein Unterprogramm bilden, das jeweils mit neuem Text TE$, neuer Zeile ZE und Spalte SP aufgerufen werden kann. So können Sie beliebigen Text in das Hochauflösungsbild schreiben.

b) Nun zum zweiten »weichen« Weg. Weil sich dieser nahezu völlig in Maschinensprache abspielt, soll hier nur das Prinzip erklärt werden. In der Serie über Assembler-Programmierung wird dieses sogenannte Interrupt-Handling besprochen. Zunächst das Programm. Tippen Sie NEW ein und dann Listing 1.

Starten Sie mit RUN und Ihr Bildschirm ist in drei Zonen aufgeteilt. Ist das Programm beendet, drücken Sie eine Taste. Sie sind auch nach dem END noch in dieser Bildschirm-Aufteilung. Sie können das leicht feststellen, wenn Sie den Cursor nach oben bewegen und ein paar Schreibversuche machen. Oder versuchen Sie mal das LIST-Kommando! Wenn Sie davon genug haben, dann geben Sie (RUN/STOP) und (RESTORE) ein, und Sie sind wieder im Normalzustand des Bildschirmes. Wenn man diese Technik beherrscht, kann man mit dem Bildschirm praktisch alles machen, was man will! Wir bedienen uns eines sogenannten Rasterzeilen-Interrupts. Ich habe Ihnen in der letzten Folge erklärt, daß der bildaufbauende Elektronenstrahl über zirka 280 Rasterzeilen huscht und 20mal in der Sekunde ein komplettes neues Bild aufbaut. In der einschlägigen Literatur ist man sich übrigens uneins: Woanders wird erzählt, es handle sich um 264 Rasterzeilen und 60 mal in der Sekunde werde ein neues Bild aufgebaut. Wie dem auch sei: Richtig ist, daß es ein enorm schneller Geselle ist, der über den Bildschirm huscht, und daß die aktuelle Rasterzeile in den Registern 53266 (LSB) und 53265, Bit7 (msb) mitgezählt wird. Interrupts bringen den Computer dazu, neben seiner uns sichtbaren Arbeit (zum Beispiel Programmablauf) noch eine Anzahl anderer Dinge zu tun. Eines davon ist die ständige Wiederauffrischung des Fernsehbildes durch Informationen an den Rasterstrahl. Der C 64 löst solche Interrupts auch per Programm aus. Zu diesem Zweck dienen die Register 53273 und 53274. Bit 7 von 53273 sagt uns, daß ein Interrupt aufgetreten ist (Bit 7 ist dann 1), mit einer der Ursachen, die noch in den Bits 0 bis 3 einzeln angegeben werden:

Bit 0= 1 Rasterzeilen-Interrupt Bit 1 = 1 Sprite/Hintergrund-Kollision Bit 2 = 1 Sprite/Sprite-Kollision Bit 3= 1 Interrupt durch Lichtgriffel.

Register 53274 bietet uns die Möglichkeit einer sogenannten Interrupt-Maske. Bis auf Bit 7 ist es genauso aufgebaut wie 53273. Wenn wir hier zum Beispiel in Bit 0 eine Eins setzen, dann weiß der VIC-II-Chip, daß er einen sogenannten Rasterzeilen-Interrupt auslösen soll. Nur dies alleine würde kaum Wirkung haben, denn nun erfolgt beim Auslösen des Interrupts ein Sprung an die Adresse, die vom Interrupt-Vektor (Speicherstellen 788 (LSB) und 789 (MSB)) angezeigt wird. Das ist im Normalfall ein Maschinenprogramm im Betriebssystem (Start bei 59963). Weil dieser Zeiger im RAM liegt, kann er verändert werden, so daß er auf ein eigenes Maschinenprogramm weist, das nun die Interruptbehandlung nach unserem Gutdünken ausführt. Außerdem müssen wir noch angeben, in welcher Rasterzeile der Interrupt stattfinden soll. Dazu schreiben wir in das Rasterregister diese Zeilennummer ein. Das ist also das Prinzip, und weil diese ganze Angelegenheit sehr schnell erledigt sein muß, ist das nur in Maschinensprache möglich.

Grafik und Maschinensprache

Wer Grafik in Basic betreibt, braucht Sitzfleisch. Das haben Sie sicherlich am eigenen Leibe bemerkt. 20 Minuten für ein fertiges 3D-Bild, das ist schon ziemlich lange! Die meisten brauchbaren Grafik-Programme sind deshalb in Maschinensprache geschrieben. In der nächsten Ausgabe wird ein einfaches aber brauchbares Grafik-Unterprogramm-Paket in Maschinensprache vorgestellt, mit dem Sie den Zeitbedarf erheblich reduzieren können. Verantwortlich für diese lange Zeitdauer von Basic-Programmen ist der Basic-Interpreter, der jeden Befehl übersetzen muß und dann ein zum Befehl gehöriges, oft recht verwickeltes Maschinenprogramm ausführt, dann den nächsten Befehl übersetzt, und so weiter… Wenn das zum Beispiel in einer FOR….NEXT-Schleife mit 320 Durchläufen passiert, dann dauert das…! Je einfacher und auch allgemein verwendbarer ein Maschinenprogramm ist (jedenfalls für Grafik), desto umfangreicher muß das Basic-Aufrufprogramm sein. Oder: Je spezialisierter ein Maschinenprogramm ist, desto weniger Basic-Aufrufprogramm ist nötig. Ein Beispiel: Wenn das Maschinenprogramm lediglich die Routine zum Berechnen und Zeichnen eines Punktes enthält, dann muß vom Basic-Aufrufprogramm eine FOR..NEXT-Schleife 320 durchlaufen werden, in der jedesmal X variiert, Y aus der Funktionsgleichung berechnet wird, beide dann transformiert werden auf das Bildschirmsystem, die transformierten Werte an die Speicheradressen gePOKEt werden, von denen es die Maschinenroutine nach dem SYS-Aufruf abholt. Man hat im Aufrufprogramm allerlei Freiheiten: Man kann nach Belieben das Koordinatensystem ändern, die zu zeichnende Funktion, den Start- und den Endwert der FOR..NEXT-Schleife und das alles relativ einfach durch einige INPUT-Anweisungen oder notfalls Programmzeilenänderungen erreichen. Dafür muß man die lange Zeitdauer des Aufrufprogrammes hinnehmen. Ein Maschinenprogramm wäre zwar sehr schnell und erforderte von Basic aus unter Umständen nur einen SYS-Befehl. Aber es wäre mehr oder weniger festgelegt auf immer diese eine Aufgabe und damit recht unbeweglich und auch ziemlich lang. Maschinenprogramme andererseits, die dieselben Eingabe- und Variationsmöglichkeiten wie das vorhin erwähnte Basic-Aufrufprogramm bieten, sind schon etwas für Feinschmecker der Assemblerprogrammierung und äußert rar. Ein anderes Phänomen ist die Tatsache, daß man vor der Wahl steht: Geschwindigkeit oder Speicherplatz sparen. Man kann Grafik-Maschinenprogramme enorm beschleunigen durch spezielle Programm-Techniken. Sie werden dann aber häufig so lang, daß man sie kaum mehr als DATA-Zeilen-Listing abdrucken kann.

Bewegte Grafik

Wie man einen Trickfilm mit Hilfe von Sprites drehen kann, habe ich Ihnen in Folge 5 gezeigt. Welche Möglichkeiten gibt es ohne Sprites? Schneller Bildaufbau — kurze Verzögerung — Bild löschen — neues Bild aufbauen mit veränderter Ansicht — und so weiter… Wenn Sie das in Basic überlegen, können Sie das gleich wieder vergessen. Um den Eindruck von Bewegung zu vermitteln, muß alles viel schneller gehen. Aber auch ein Maschinenprogramm muß sehr sorgfältig entwickelt werden, um die nötige Geschwindigkeit des Bildaufbaues zu erhalten. Für einfache Darstellungen könnte dieses Konzept aber funktionieren. Denken Sie aber zum Beispiel mal an unsere 3D-Bilder! Mit dem C 64 — behaupte ich — geht’s so nicht. Stellen Sie sich vor, wir benützen mehrere Bit-Maps und Bildschirme und zeichnen in je eine Bit-Map einen Bewegungszustand unseres Bildes. Dann müssen wir nur noch in einer Aufrufschleife von Bit-Map zu Bit-Map umschalten. Das ist auch in Basic möglich. Wir hätten dann drei Bit-Maps zur Verfügung. Das ist zwar nicht viel, aber immerhin könnte man damit schon eine Raumfläche in zwei Richtungen kippen oder ähnliches. Wenn man in Maschinensprache programmiert, hat man sogar 5 Bit-Maps (mindestens) zur Verfügung und weil auch noch alles schneller geht, kann man mit einigem Geschick vielleicht sogar während man vier Bilder nacheinander zeigt, das fünfte Bild ungesehen aufbauen und auf diese Weise mehr als fünf Bewegungsstadien realisieren. Sie sehen aber schon: Das ist die hohe Schule der Programmierkunst und hier gibt es noch viel zu tun. Einen 3D-Trickfilm auf diese Weise zu erzeugen, ist heute auch auf großen Computern noch kaum möglich. Der Film TRON beispielsweise setzt sich aus lauter per Computer erzeugten Einzelbildern zusammen, die erst filmtechnisch zum Bewegungsablauf aneinandergehängt wurden. Dort wo Echtzeit-Darstellung notwendig ist, bei Simulationen beispielsweise in Flugtrainern, reduziert man die Darstellung auf das unbedingt notwendige und hat außerdem dazu Computer zur Verfügung, die uns C 64-Benutzern das Wasser im Mund zusammenlaufen lassen. Aber was solls. Die Kunst des Programmierens liegt ja vielleicht darin, daß man mit einem Minimum an Aufwand einen Maximaleffekt erzielt. Und wenn man sich dann mal ansieht, was wir aus unserem C 64 alles herausholen können, dann stehen wir eigentlich ganz gut da, meinen Sie das nicht auch?