Assembler ist keine Alchimie – Teil 3
In den ersten beiden Folgen unseres Assembler-Kurses mußten Sie noch mit Basic-Ladern arbeiten. Jetzt steht Ihnen ein leistungsfähiger Monitor zur Verfügung, der SMON. Somit können Sie alle Beispiele direkt eingeben und ausprobieren.
In der letzten Folge haben wir die ersten Assembler-Befehle kennengelernt und wissen, wie man sie benutzt und was sich im Computer dabei tut. Die Zahlen der Assembler-Alchimisten haben uns einige Geheimnisse enthüllt, obwohl sie für die Zweifingerlinge und die Sechzehnfingerlinge gedacht sind. Die Binärzahlen können wir schon zusammenzählen. Heute werden Sie eine Reihe weiterer Assembler-Befehle kennenlernen und noch ein weiteres Zahlensystem. Wir ergründen das Geheimnis der negativen Zahlen und machen uns die Funktion der Flaggen zunutze.
Wir haben nun auch einen sehr brauchbaren Assembler für den C 64: Den SMON, dessen 1. Teil in dieser Ausgabe abgedruckt ist. Künftig wird in dieser Serie die SMON-Syntax verwendet und kein Basic-Lader mehr angegeben. Außerdem hat in Ausgabe 9 die Serie »Der gläserne VC 20« begonnen, so daß sich der Schwerpunkt hier mehr auf den C 64 verlagert. Das sollte aber die VC 20-Fans nicht davon abhalten, diesen Kurs weiter zu verfolgen, denn bis auf gelegentliche Adreßänderungen ist fast alles für sie verwendbar.
Eine Zauberformel der Assembler-Alchimisten: INX, INY, INC, DEX, DEY, DEC?
Wir wissen ja schon, daß man diese »Zauberformeln« entzaubern kann. INX heißt einfach »increment X-Register«, also Inhalt des X-Registers um 1 erhöhen. Es wird Ihnen sicher einleuchten, daß INY dasselbe mit dem Y-Register tut. Etwas weniger deutlich ist das bei INC. Das bedeutet »increment memory«, also zähle zum Inhalt einer Speicherstelle eins dazu. INX und INY enthalten alles, was dem Computer zu sagen ist, sind also offensichtlich 1-Byte-Befehle mit der in der letzten Folge schon kennengelernten impliziten Adressierung. Bei INC muß dem Computer noch gesagt werden, welche Speicherstelle er um 1 erhöhen soll. Es gehört also noch eine Adresse dazu. Das läßt diesen Befehl im allgemeinen zu einem 3-Byte-Befehl werden.
Befehle zum Zählen
Das umgekehrte leisten die Befehle DEX, DEY und DEC. Sie bedeuten nämlich »decrement X-Register«, also »zähle das X-Register um eins herunter«, beziehungsweise das Y-Register oder — bei DEC — die angegebene Speicherstelle. Für die Adressierungsart und die Anzahl Bytes pro Befehl gilt hier das gleiche wie für die INX…-Befehle. Sehen wir uns das an einem kleinen Beispiel an: Bitte lesen Sie sich dazu die Bedienungshinweise zum SMON durch.
1500 LDA #00
1502 LDX #01
1504 STA D800
1507 STX 0400
150A INX
150B STA D801
150E STX 0401
1511 DEX
1512 STA D802
1515 STX 0402
1518 BRK
Wenn Sie das kleine Programm mit G 1500 starten, dann sollten Sie in der linken oberen Ecke des Bildschirms ABA in schwarzer Schrift stehen haben. Was ist geschehen? Wir haben den Inhalt des Akku (= 0, also Farbcode für schwarz) in das Bildschirm-Farbregister geschrieben (#D800), dann den Inhalt des X-Registers (1 = POKE-Code für den Buchstaben A) in die erste Bildschirm-Speicherzelle (#0400). Anschließend wurde das X-Register um 1 erhöht (2 = POKE-Code für den Buchstaben B) und dieser Inhalt in die zweite Bildschirmzelle geschrieben. Außerdem mußte natürlich auch dieser Bildschirm-Farbspeicherplatz mit dem Farbcode 0 belegt werden. Durch DEX wurde das X-Register wieder herunter gezählt, somit wieder ein A erzeugt und in die dritte Bildschirmstelle gedruckt.
Sie haben sicher schon bemerkt, daß man auf diese Weise Abläufe mitzählen kann. Soll zum Beispiel ein Vorgang 20 mal wiederholt werden, dann packt man ins X-Register (oder ins Y-Register oder in eine andere Speicherstelle) den Anfangswert 0, läßt den Computer eine Arbeit ausführen, erhöht das entsprechende Register oder die Speicherzelle um 1 mit INX, INY oder INC, prüft dann, ob dieser Inhalt schon 20 geworden ist und so weiter. Wie man diese Prüfung vornimmt, dazu kommen wir erst später bei den BRANCH-Befehlen. Das ist also ähnlich wie im Basic bei den FOR…NEXT-Schleifen: Dort wird eine Variable als Zähler verwendet, hier ein Register (oder eine Speicherstelle). Ebenso wie im Basic bei diesen Schleifen kann man auch hier rückwärts zählen mit DEX, DEY oder DEC. Das hat oft gewisse Vorzüge, was uns aber noch nicht kümmern soll.
Wenn wir diese Befehle als Zähler verwenden, sollten wir im Auge behalten, daß eine Speicherstelle (auch ein X- oder Y-Register) Zahlen nur von 0 bis 255 enthalten kann. Die höchste 8-Bit-Zahl ist ja:
| dez. 255 = | bin. 1111 1111 |
| +1 | 1 |
| –––––––––––––– + | |
| ergibt: | (1) 0000 0000 |
Wenn wir also über 255 hinauszählen, ergibt sich wieder 0 und so weiter, weil ein Überlauf stattgefunden hat. Das 9.Bit paßt nicht mehr in das Byte hinein. Um nochmal genau sehen zu können, was unser Computer da tut, probieren Sie einmal aus:
1500 LDA #01
1502 BRK
Das soll uns die Register zunächst mal im Ausganszustand zeigen. Nach G 1500 werden sie angezeigt:
| AC | XR | YR | N | V | - | B | D | I | Z | C |
| 01 | 00 | 00 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 0 |
Im Akku steht jetzt die dort eingeladene 1. Nun wollen wir das X-Register laden mit 255 (also $FF). Dazu ändern wir das Programm:
1502 LDX #FF
1504 BRK
Nach erneutem G 1500 zeigen die Register:
| AC | XR | YR | N | V | - | B | D | I | Z | C |
| 01 | FF | 00 | 1 | 0 | 1 | 1 | 0 | 0 | 0 | 0 |
Im X-Register steht nun die Zahl $FF. Bei den Flaggen hat sich die N-Flagge (die negative Zahlen anzeigen soll) auf 1 geschaltet!
Nun wollen wir das X-Register über 255 hinauszählen. Wir verändern das Programm nochmal:
1504 INX
1505 BRK
Der Start mit G 1500 liefert uns die folgende Registeranzeige:
| AC | XR | YR | N | V | - | B | D | I | Z | C |
| 01 | 00 | 00 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 0 |
Wie erwartet, ist der Überlauf des X-Registers eingetreten: Es ist jetzt Null. Die N-Flagge hat ihren gewohnten Wert 0 wieder angenommen und die Z-Flagge, die uns anzeigt, ob die letzte Operation eine Null erzeugt hat, ist jetzt gesetzt. Bei weiterem Hochzählen verschwindet die Z-Flagge wieder:
1505 INX
1506 BRK
G 1500 liefert den Registerinhalt:
| AC | XR | YR | N | V | - | B | D | I | Z | C |
| 01 | 01 | 00 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 0 |
Das gleiche passiert bei Verwendung des Y-Registers als Zähler, wie Sie leicht durch Austauschen aller auf X bezogenen Befehle feststellen können. Sehr nett ist es, diesen Befehlsablauf einmal für den INC-Befehl auf die Speicherstelle $0400 (Bildschirmspeicher links oben) bezogen ablaufen zu lassen. Wenn man darauf achtet, daß kein Hochscrollen des Bildschirms eintritt, kann man das Ergebnis außer in den Registern auch noch als Zeichen auf dem Bildschirm verfolgen. Der Beginn der Befehlsequenz ist dann sinnvollerweise:
1500 LDA #FF
1502 STA 0400
1505 BRK
Im folgenden setzt man dann anstelle von INX immer INC 0400 ein.
Was passiert beim Herunterzählen unter Null? Sie können das mit der gezeigten Befehlskette leicht verfolgen, indem Sie immer statt INX jetzt DEX setzen und die Register nicht mit $FF, sondern mit 01 laden. Es zeigt sich, daß beim Herabzählen nach der Null wieder 255 (= $FF) im Register zu finden ist. Die Reaktion der N- und der Z-Flagge auf den jeweiligen Registerinhalt ist die gleiche wie beim Hochzählen.
Es ist uns nun deutlich, daß diese sechs Befehle die N-Flagge und die Z-Flagge beeinflussen können. Diese Tatsache wird später noch eine große Rolle spielen, wenn es um die bereits erwähnte Schleifenkontrolle geht.
Noch ein alchimistischer Zahlentrick
Die Assembler-Alchimisten haben noch viel mehr Arten der Zahlen- und Zeichendarstellung auf Lager. Eine davon ist die Codierung als BCD-Zahlen. BCD kommt vom englischen »binary coded dezimal«, was bedeutet: Binär codierte Dezimalzahlen.
Zwischendurch möchte ich noch eine Bemerkung loswerden, die Sie als Trost auffassen sollen: Auch wenn wir später andere Zahlendarstellungen kennenlernen werden, es wird nicht so schwierig! Sogar so komplette Idioten wie Computer verstehen das, obwohl man ihnen alles haarklein vorkauen muß.
Wenden wir uns nun wieder den lächerlich einfachen BCD-Zahlen zu. Alle Zahlen von 0 bis 9 lassen sich binär mit nur 4 Bits ausdrücken:
| Binär | Dezimal |
| 0000 | 0 |
| 0001 | 1 |
| 0010 | 2 |
| 0011 | 3 |
| 0100 | 4 |
| 0101 | 5 |
| 0110 | 6 |
| 0111 | 7 |
| 1000 | 8 |
| 1001 | 9 |
Die weiteren Werte 1010 bis 1111 werden in der BCD-Codierung nicht benutzt. Liegt nun eine Dezimalzahl (zum Beispiel 12) vor, dann wird jede Stelle dieser Zahl (also die 1 und die 2) getrennt binär codiert. In unserem Beispiel mit der 12 wäre das dann 0001 für die 1 und 0010 für die 2. Somit ist die 12 im BCD-Code 0001 0010. Jede Ziffer erhält so ihr Nibble. Eine Zahl im BCD-Format hat deswegen keine feste Anzahl von Bytes, sondern die Byte-Zahl hängt von der Anzahl der Stellen ab. Die Zahl 1984 beispielsweise braucht 2 Bytes: 0001 1001 1000 0100.
Schwierig gestaltet sich das Rechnen mit diesen Zahlen wegen der sechs unbenutzten Codes. Aber auch da habe ich einen Trost für Sie: Wir werden damit nicht rechnen. Wozu das ganze dann, werden Sie sich fragen? Der Grund für das alles ist, daß BCD-Zahlen im Gegensatz zu den Zahlen mit festem Format (die sonst verwendet werden) so eingegeben und verarbeitet werden können, wie sie vorliegen. Das ist im kaufmännischen Bereich manchmal notwendig, wo eben 1000mal 0,1 Pfennige 1 Mark ergeben und Fehler unzulässig sind. Sollten Sie also vor dem Problem stehen, mit BCD-Zahlen rechnen zu müssen, grämen Sie sich nicht: Unser Prozessor kennt den Dezimalmodus. Er ist dann eingeschaltet, wenn die Dezimal-Flagge auf 1 gesetzt ist.
Damit sollen Sie dann auch noch gleich zwei neue Befehle kennenlernen: SED und CLD. Der erstere hat nichts mit Parteien zu tun, sondern ist die Abkürzung für »Set dezimal-flag«, also setze die Dezimalflagge. So schalten Sie den Dezimal-Modus ein. Wie Sie sicher schon messerscharf geschlossen haben, heißt CLD »Clear dezimal-flag«, also setze die Dezimalflagge auf Null, wodurch dieser Modus wieder auszuschalten ist.
Wichtig! Wenn Sie argwöhnen, daß in einem Programm irgendwann mal die Dezimal-Flagge gesetzt sein könnte, dann gehen Sie auf Nummer sicher und schieben vor eine Rechenoperation, die nicht im Dezimalmodus laufen soll, ein CLD.
Beide Befehle sind 1-Byte-Befehle mit implizierter Adressierung. Sie beeinflussen lediglich die Dezimalflagge.
Das Geheimnis der negativen Binärzahlen
Wie schon mal betont: Der Computer ist strohdumm. Er kann nicht einmal auf normale Weise voneinander abziehen! Deswegen geht er den komplizierten Weg: Er addiert eine negative Zahl. Nur: Wie sehen negative Binärzahlen aus? Wir werden diese Frage in drei Etappen beantworten.
- Man könnte eine Flagge setzen, die 1 ist bei negativen und 0 bei positiven Zahlen. Bei einigen Fließkommazahlen wird das auch so gemacht. Hier aber setzt man die Flagge direkt in die Zahl ein: Bit 7 jeder Zahl ist jetzt ein Vorzeichenmerkmal. Wenn dieses Bit 0 ist, handelt es sich um eine positive, wenn es 1 ist, um eine negative Zahl. Auf diese Weise ist also +1 wie bisher 0000 0001, wohingegen —1 jetzt 1000 0001 hieße. Damit wird allerdings der Zahlenbereich, der durch ein Byte auszudrücken ist, verschoben. 255 = binär 1111 1111 kann so nicht mehr verwendet werden. Die größte Zahl, die jetzt ausgedrückt werden kann, ist 0111 1111 = dezimal 127. Die kleinste Zahl ist dann 1111 1111 = —127. Probieren wir mal aus, wie sich damit rechnen läßt:
ergibt 1001 0000 = –16,+10 0000 1010 –6 1000 0110 ––––––––––– +
was offensichtlich falsch ist, denn nach Adam Riese sollte +4 herauskommen. So kann man also nicht rechnen!Man nennt diese Art der Zahlendarstellung, übrigens »signed binary«-Format, also in Deutsch: markierte Binärzahlen.
- Der nächste Schritt ist das sogenannte Einerkomplement. Dabei tritt für die positiven Zahlen keine Änderung ein. Die negativen entstehen aus den positiven durch
Komplementbildung, das heißt jedes Bit der positiven Zahl wird in sein Gegenteil verkehrt, wie es das folgende Beispiel zeigen soll:
0000 1100 ist +12,dann ist das Einerkomplement:
1111 0011 = –12.Komplement ist nicht kompliziert
Interessanterweise taucht hier auch wieder das Merkmal der »signed binary«-Zahlen auf: die 1 in Bit 7 bei negativen Zahlen. Beschränkt man sich auf den Zahlenbereich, der für die »signed binary«-Zahlen gültig war, dann hätten wir jetzt beide Darstellungsweisen miteinander vereint. Nun müssen wir natürlich noch feststellen, ob man so auch rechnen kann.
was 1 mit einem Übertrag ergäbe, jedenfalls nicht 2, wie's sich gehört. Also ist auch die Einerkomplementdarstellung noch nicht das Gelbe vom Ei.+8 0000 1000 –6 1111 1001 in Einerkomplementdarstellung –––––––––––––––––– + ergibt (1) 0000 0001 - Ich will Sie nicht länger auf die Folter spannen: Wenn man zum Einerkomplement einer Zahl noch 1 dazuzählt, erhält man das Zweierkomplement. Und genau so werden negative Zahlen in unserem Computer gehandhabt. Die positiven Zahlen bleiben unverändert. Von den negativen bildet man das Zweierkomplement wie zum Beispiel hier mit der Zahl –12:
12 0000 1100 normale Binärdarstellung (–12) 1111 0011 Einerkomplement +1 0000 0001 addieren ––––––––––––––– (–12) 1111 0100 Zweierkomplement Jetzt wollen wir auch diese Zahlenart ausgiebig testen:
Wir rechnen nochmal 8-6:
also 2 mit einem Übertrag, der ignoriert wird. Das Ergebnis ist richtig. Wenn bei einer solchen Rechnung eine negative Zahl herauskommt, ist sie nicht leicht zu erkennen. In solchen Fällen kehrt man das Vorzeichen um, indem man das Zweierkomplement berechnet. Das machen wir mal am Beispiel 5—6:+8 0000 1000 –6 1111 1010 das ist –6 in der Zweierkomplementdarstellung. ––––––––––––––––– + ergibt (1) 0000 0010
das ist —1 in der Zweierkomplementdarstellung. Zur Kontrolle nun die Vorzeichenumkehr durch Umrechnen ins Zweierkomplement:+5 0000 0101 –6 1111 1010 das ist wieder unser Zweierkomplement von 6, also —6 –––––––––––––– + ergibt 1111 1111
also wie erwartet +1.Einerkomplement davon 0000 0000 plus 1 0000 0001 ––––––– + ergibt 0000 0001
Auf diese Weise rechnet unser Computer mit negativen Zahlen. Negative ganze Zahlen speichert er im Zweierkomplement-Format. Auch wenn wir nun etwas vorgreifen müssen, wollen wir uns das ansehen. Dazu schalten Sie am besten erst einmal den Computer aus und laden dann den SMON beziehungsweise ihren Assembler. Dann bauen wir ein kleines Basic-Programm:
10 A% = -12
20 END
Wie Variable im Speicher stehen
Noch nicht RUN eingeben! Zuerst schalten Sie den Maschinensprachmonitor ein und wir sehen uns das Programm so an, wie es im Speicher steht. Der Basic-Speicher des C 64 beginnt im Normalfall bei $0800. Wir geben also den Monitorbefehl
M 0800
Uns genügen schon die Speicherplätze bis $081C. Nun sehen wir das nackte Basic-Programm im Speicher, so wie es uns C. Sauer in seinem Artikel »Der gläserne VC 20, Teil 1« im 64'er, Ausgabe 9/84 auf Seite 156 beschrieben hat.
In Bild 1 ist unser Speicherinhalt kommentiert zu sehen. Das Programm endet im Speicherplatz $0813. Das Kennzeichen für Programmende sind zwei aufeinanderfolgende Bytes mit dem Wert Null. Dahinter werden die Variablen abgelegt, sobald das Programm gestartet wird. Wir steigen aus dem Monitor durch X aus und starten das Programm mit RUN. Jetzt sehen wir nochmal in den Speicher. Bis $0813 hat sich nichts verändert. Danach aber ist jetzt in 7 Bytes die Variable A% abgelegt. Das zeigt Bild 2.
| 0800 | 00 | 0C | 08 | 0A | 00 | 41 | 25 | B2 |
| 080C Koppeladresse |
000A Zeilennr.10 |
A | % | = Token |
||||
| 0808 | AB | 31 | 32 | 00 | 12 | 08 | 14 | 00 |
| – Token |
1 | 2 | Zeilen- ende |
0812 Koppeladresse |
0014 Zeilennr.20 |
|||
| 0810 | 80 | 00 | 00 | 00 | FF | FF | FF | FF |
| END Token |
Zeilen- ende |
Programm- ende |
Leerer Speicher | |||||
| Speicherstelle | 0814 | 0815 | 0816 | 0817 | 0818 bis 081A |
| Byte | 1 | 2 | 3 | 4 | 5-7 |
| Inhalt | C1 | 80 | FF | F4 | 00 00 00 |
| 1100 0001 | 1000 0000 | 1111 1111 | 1111 0100 | unbenutzt bei Integerzahlen | |
| Kennbits 7 für Integer | MSB | LSB | |||
| 0100 0001 ≙ 65 Code für A |
0000 0000 | von -12 |
|||
| Variablenname und -typ Variablenwert |
|||||
Zunächst einmal die Bytes $0814 und $0815: Hier wird der Variablenname und der -typ angegeben. Der Typ ist aus den Bits 7 zu erkennen. Sind beide (wie hier) gleich 1, dann handelt es sich um eine Integervariable (also eine ganze Zahl). Läßt man die Kennbits außer acht, zeigt sich, daß in $0814 der Code für den Buchstaben A steht und $0815 nur den Wert 0 enthält. Nun zum Rest: Der C 64 legt Integers in nur 2 Bytes ab — die restlichen 3 Bytes $0818 bis $081A bleiben unbenutzt. Das ist auch dann der Fall, wenn danach noch weitere Variable kommen. Es bringt also keine Speicherersparnis (VC 20-Benutzer aufgepaßt!), wenn man mit Ganzzahlvariablen arbeitet!
In $0817 steht $F4, welches binär ausgedrückt 1111 0100 ist. Das kennen wir noch von weiter oben als die —12 im Zweierkomplement-Format. Woher kommt $FF in Speicherzelle $0816? Wie gesagt, die Integers werden in 2 Bytes gespeichert, und wenn wir —12 in 16 Bits ausdrücken, dann sieht das so aus:
| +12 | 0000 0000 | 0000 1100 | |
| Einerkomplement: | 1111 1111 | 1111 0011 | |
| +1 | 0000 0000 | 0000 0001 | |
| ––––––––––––––––––––––––––––––––––––– | |||
| ergibt –12 | 1111 1111 | 1111 0100 | als 16-Bit-Zweierkomplement. |
| MSB=$FF | LSB=$F4 | ||
Die größte positive ganze Zahl, die man in 2 Bytes ausdrücken kann, ist 32767, was binär
0111 1111 1111 1111
ergibt. Die kleinste ist
1000 0000 0000 0000
also —32768. Das ist der Grund dafür, daß der C 64 Integers größer als 32767 oder kleiner als —32767 dankend mit ILLEGAL QUANTITY ERROR ablehnt, wenn sie als Argument verwendet werden. (Die Zahl —32768 kann als Ergebnis von logischen Operationen durchaus auftauchen.)
Damit will ich Sie für diesmal von den Zahlenspielereien erlösen. In der nächsten Folge müssen wir darauf nochmal zurückkommen. Sie können die Art des Abziehens von Zahlen durch Addieren des Zweierkomplementes bis zum nächsten Mal an weiteren Beispielen üben. Wenn Sie das mit 16-Bit-Zahlen tun, werden Sie bald feststellen, daß noch nicht alles so funktioniert wie es sollte…
Wir können jetzt übrigens auch das Rätsel lösen, weshalb bei positiven Zahlen (zum Beispiel LDA #FF) die Negativ-Flagge auf 1 geht: Die Flagge wird immer dann gezückt, wenn eine Zahl auftritt, die in Bit 7 eine 1 aufweist. Ganz einfach, gell?
Ein wirkungsvolles Zweiglein: BNE
Vermutlich raucht Ihnen nach soviel Zahlensalat der Kopf. Deshalb sollen Sie zur Entspannung noch einen neuen Assembler-Befehl kennenlernen und auch gleich ein nützliches Programmbeispiel dazu.
BNE heißt »branch if not equal zero«, was man übersetzen kann mit »verzweige, wenn ungleich Null«. Genauer gesagt: Es wird dann verzweigt — also zu einer angegebenen Adresse gesprungen —, wenn die Z-Flagge (die haben wir bei den INX,DEX…-Befehlen genauer untersucht) nicht gesetzt ist, also 0 zeigt. Sehen wir uns das mal an der nachfolgenden Verzögerungsschleife an, deren Flußdiagramm Bild 3 zeigt.
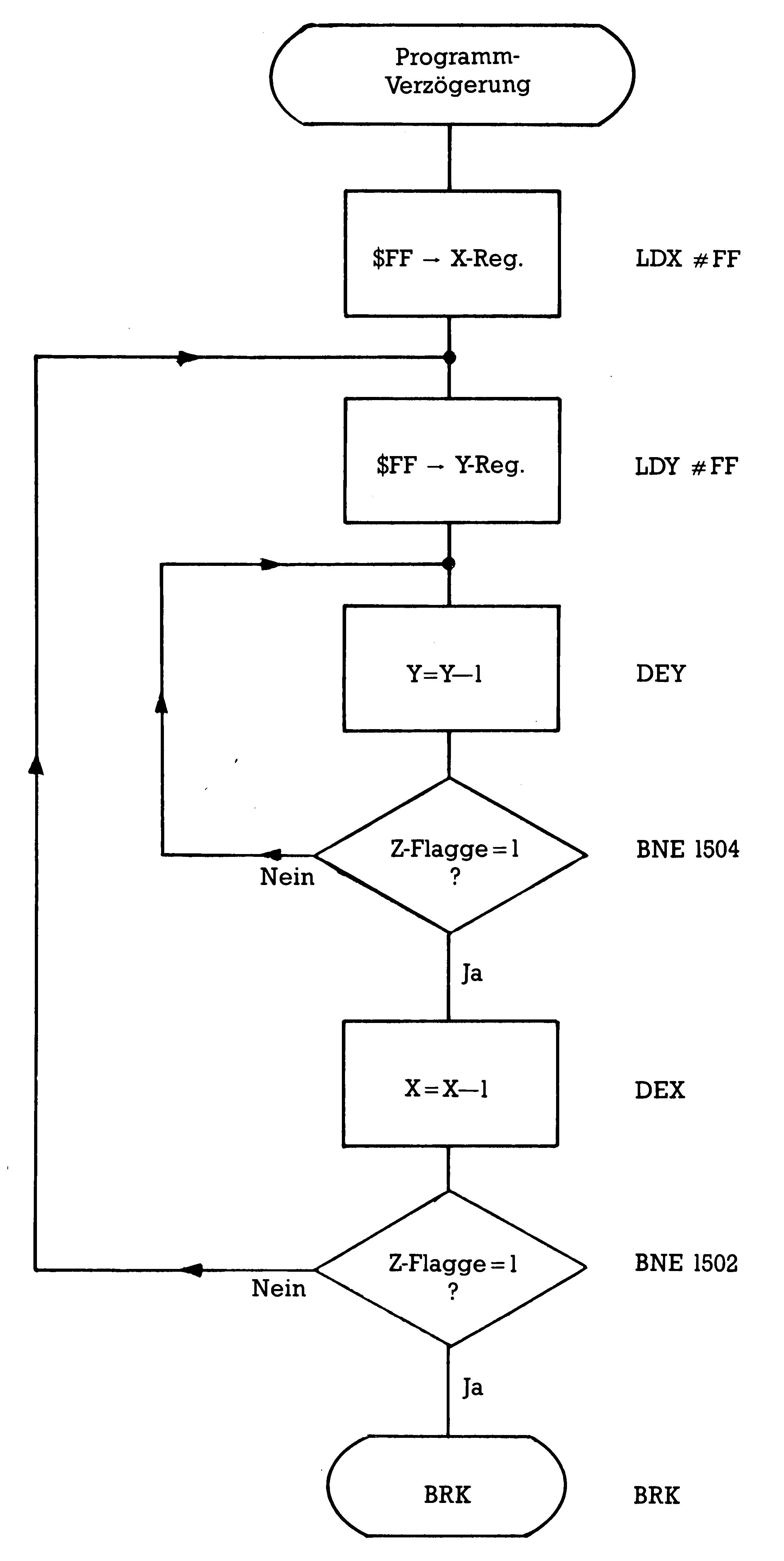
Das Progrämmchen dazu:
1500 LDX #FF
1502 LDY #FF
1504 DEY
1505 BNE 1504
1507 DEX
1508 BNE 1502
150A BRK
Zunächst einmal werden das X- und das Y-Register als Zähler initialisiert (also mit einem Ausgangswert geladen). Mit dem vorhin behandelten Befehl DEY wird dann das Y-Register um 1 heruntergezählt, was jetzt $FE ergibt. Für die Nullflagge (Z) bedeutet das den Inhalt 0, denn es liegt kein Grund vor, sie zu setzen (also eine 1 dort anzuzeigen), weil noch keine Null aufgetreten ist. Bei der nachfolgenden Prüfung durch BNE wird also eine Verzweigung nach 1504 das Ergebnis sein, worauf das Y-Register weiter verringert und dann die Z-Flagge erneut geprüft wird und so weiter. Das geht so lange, bis nun wirklich endlich die Null im Y-Register erreicht ist. In diesem Fall zählt DEX nun das X-Register herunter und der nächste BNE-Befehl führt zum Sprung nach 1502, wo das Y-Register wieder auf $FF gesetzt wird. Auf diese Weise wird die äußere Schleife 255mal und die innere 65025mal durchlaufen.
Kein Widerspruch: Assembler-Programme langsamer machen
Sie haben beim Eingeben des Programmes vermutlich etwas gestutzt, als der Assembler nach dem BNE 1504 als nächste Adresse statt dem erwarteten 1508 eine 1507 ausgegeben hat. Der Befehl sieht zwar wie ein 3-Byte-Befehl aus, ist aber nur ein 2-Byte-Befehl! Das liegt an der speziellen Art der Adressierung von solchen Branch-Anweisungen: Der sogenannten relativen Adressierung, die wir aber erst später mit den anderen Branch-Befehlen behandeln werden.
Wenn Sie das Programm mit G 1500 starten, werden Sie — obwohl alles in Maschinensprache schnell läuft — eine merkliche Verzögerung feststellen, bevor die Registeranzeige auftaucht. Noch längere Verzögerungen lassen sich ohne weiteres erreichen, indem man mehr Schleifen ineinanderschachtelt. Dabei verwendet man dann den DEC-Befehl.
In der Tabelle sind auch die Zyklen angegeben, die die heute neu gelernten Befehle zur Abarbeitung benötigen. Mit solchen Angaben lassen sich recht genau definierte Zeiten einstellen, in denen der Computer nichts anderes tut als durch das Programm zu flitzen. Wozu das dient, braucht wohl kaum noch gesagt werden: Wenn Sie zum Beispiel einen Text auf dem Bildschirm lesen wollen, bevor das Programm weiterläuft oder wenn Sie mit Peripherie arbeiten, die langsamer als das Programm ist oder… Allerdings muß noch gesagt werden, daß es noch elegantere Methoden zur Verzögerungs-Programmierung gibt als das Lahmlegen des Computers, aber dazu kommen wir erst in einer späteren Folge.
(Heimo Ponnath/gk)|
Befehlswort |
Adressierung |
Byteanzahl |
Code | Dauver in Taktzyklen |
Beeinflussung von Flaggen |
|
| Hex | Dez | |||||
| INX | implizcit | 1 | E8 | 232 | 2 | N,Z |
| INY | implizit | 1 | C8 | 200 | 2 | N,Z |
| INC | absolut | 3 | EE | 238 | 6 | N,Z |
| DEX | implizit | 1 | CA | 202 | 2 | N,Z |
| DEY | implizit | 1 | 88 | 136 | 2 | N,Z |
| DEC | absolut | 3 | CE | 206 | 6 | N,Z |
| SED | implizit | 1 | F8 | 248 | 2 | 1 → D |
| CLD | implizit | 1 | D8 | 216 | 2 | 0 → D |
| BNE | relativ | 2 | D0 | 208 | 2 +1 bei Verzweigung + 2 bei Überschreiten einer Seitengrenze |
– |
