Assembler ist keine Alchimie – Teil 4
In dieser Folge des Assembler-Kurses lernen Sie die wichtigen Arithmetik-Befehle des Prozessors kennen. Anhand von Beispielen und Übungen können Sie alle Schritte am Computer miterleben. Außerdem wird die Frage geklärt, wie Assembler-Programme in Basic eingebunden werden.
Neun neue Befehle haben wir in der letzten Folge kennengelernt und wir wissen nun, wie unser Computer ganze Zahlen (sogenannte Integers) abspeichert. Zur Erinnerung: Das geschieht im Zweierkomplement-Format. Das Bit 7 einer 8-Bit-Zahl dient dabei als Vorzeichen-Merkmal: Wenn es 0 ist, liegt eine positive Zahl vor, die genauso aussieht, wie wir bislang immer Binärzahlen kannten. Ist das Bit 7 aber eine 1, dann haben wir es mit einer negativen Zahl in der Zweierkomplement-Darstellung zu tun. Wenn wir — wie unser Computer — zur Verarbeitung ganzer Zahlen 16 Bits (also 2 Bytes) verwenden, dann isf eben Bit 15 anstelle von Bit 7 das Vorzeichenbit.
Wenn Sie nun am Ende der letzten Folge ein bißchen mit solchen Zahlen gerechnet haben, konnten Sie sicher feststellen, daß zwar oft das richtige Ergebnis herauskam — aber leider nicht immer. Warum das so ist und was man deswegen noch beim Arbeiten mit Zahlen per Computer beachten muß, soll in dieser Folge dran sein. Damit wir aber nicht nur im vergleichsweise trockenen Zahlendschungel herumirren, sollen Sie heute endlich auch die wichtigsten Befehle des 6502 (beziehungsweise 6510) zur Arithmetik kennenlernen. Außerdem gibt es dazu noch zwei Flaggen gratis und die Branch-Befehle (schon lange überfällig) sollen Ihnen nun vertraut werden. Zunächst aber noch etwas Zahlensalat:
Herr Carry und der V-Mann
Keine Angst, wir sind nicht ins Krimi- oder Agentenmilieu gewechselt! Wir haben es mit zwei Flaggen zu tun, der Carry- und der V-Flagge. »To carry« heißt auf deutsch etwa »tragen«. In der Registeranzeige ist diese Flagge immer mit C gekennzeichnet. Was wird denn hier getragen? Das ergründen wir am besten an einem Beispiel. Dazu rechnen wir mit normalen Binärzahlen (also ohne Rücksicht auf Vorzeichenbits). Wir zählen die Zahlen 128 und 130 zusammen:
| 128 | 1000 0000 | ||
| + | 130 | + | 1000 0010 |
| 258 | (1) 0000 0010 | ||
Das Ergebnis 258 ist richtig — auch in der Binärdarstellung — nur es paßt nicht mehr in 8 Bits. Ein Bit wurde überTRAGEN in ein extra dafür vorgesehenes Plätzchen: In das Carry-Bit. Jedesmal also, wenn so ein Übertrag in einer Rechenoperation des C 64 stattfindet, zeigt die Carry-Flagge eine 1 (Bild 1).
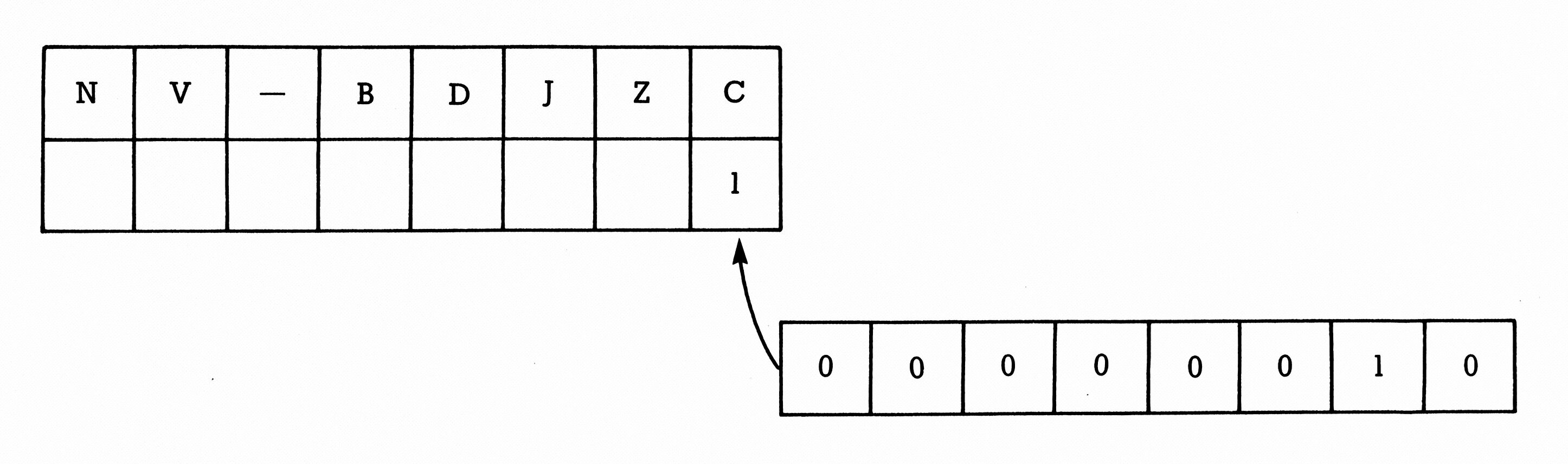
Je nach Art der von uns programmierten Aufgabe können wir nun dieses Carry-Bit weiterverarbeiten. Es gibt Situationen, in denen man es einfach ignorieren darf (dazu kommen wir gleich noch) oder aber solche, wo man es weiter in der Rechnung verwendet. Schließlich kann es auch noch einen Fehler anzeigen: Dann nämlich, wenn das größte zulässige Ergebnis 1111 1111 sein darf. Natürlich kann das Carry-Bit auch gesetzt werden, wenn man in der Zweierkomplementform rechnet. Die Verhältnisse sind dann aber für ein leicht überschaubares Beispiel des Übertrages zu verwickelt, wie Sie gleich sehen werden.
Wenn wir nämlich mit den Zweierkomplement-Zahlen rechnen, dann interessieren uns auch Fälle wie bei der Addition von 64 und 66:
| 64 | 0100 0000 | ||
| + | 66 | + | 0100 0010 |
| (—126) | 1000 0010 | ||
Das ist offensichtlich falsch. Bei der Addition ist durch das Zusammenzählen der Bits 6 plötzlich Bit 7 gesetzt worden. Da wir es aber mit einer Zweierkomplementzahl zu tun haben, bei der dieses Bit 7 eine negative Zahl anzeigt, folgt ein Fehler. Es ist also von Bedeutung, so einen Überlauf (englisch: ‘overflow’) erkennen zu können um eine entsprechende programmtechnische Reaktion zu starten. Es wird die Überlauf-Flagge V auf 1 gesetzt. Leider ist die Sache aber nicht so einfach, daß sie immer gesetzt würde, wenn von Bit 6 nach Bit 7 ein Übertrag stattfindet. Gesetzt wird diese V-Flagge nur in folgenden zwei Fällen:
- Es findet ein Übertrag von Bit 6 nach Bit 7 statt, aber kein äußerer Übertrag (wie beim Carry)
- Es findet kein interner Übertrag von Bit 6 nach Bit 7 statt, aber ein äußerer Übertrag passiert.
Merken kann man sich das am besten so: Immer dann, wenn gewissermaßen das Vorzeichenbit 7 »versehentlich« verändert wurde, wird die V-Flagge auf 1 gesetzt. Das ist ein harter Brocken! Wir sind es ja gewohnt, daß wir uns um diese Dinge beim Computer eigentlich gar nicht mehr kümmern müssen. Außerdem würde das ja erfordern, daß man sich bei allen Operationen vorher überlegen muß, welche Zahlen auftreten können und welche Fehler also durch »versehentliches« Vorzeichenändern passieren können! Genauso ist es — in der Programmierpraxis wird Ihnen aber das ganze Problem nicht mehr so groß vorkommen. Wir wollen uns dieses Zusammenspiel der Überträge von Bit 6 nach Bit 7 und von Bit 7 nach Bit 8 (also ins Carry-Bit) noch anhand einiger Beispiele klarer machen.
Im obigen Beispiel der Addition von 64 und 66 haben wir einen Fall schon behandelt: Es fand ein Übertrag von Bit 6 nach Bit 7 statt, aber kein äußerer Übertrag ins Carry-Bit. Deswegen wurde dann auch die V-Flagge gesetzt. Das Problem läßt sich hier ganz einfach lösen zum Beispiel durch Verwendung von 16-Bit-Zahlen:
| 64 | 0000 0000 0100 0000 | ||
| + | 66 | + | 0000 0000 0100 0010 |
| 130 | 0000 0000 1000 0010 | ||
Bei 16-Bit-Zahlen ist ja Bit 15 das Vorzeichenbit, welches hier keine Änderung erfährt.
Der andere Fall tritt auf bei der Addition von zwei negativen Zahlen wie —125 und —64:
| —125 | 1000 0011 | ||
| —64 | 1100 0000 | ||
| (+67) | (1) 0100 0011 | ||
Auch das ist offensichtlich falsch: Es hat wieder »versehentlich« ein Vorzeichenwechsel stattgefunden. Dies ist also der Fall, wo zwar ein Übertrag ins Carry-Bit stattfand aber kein Übertrag von Bit 6 nach Bit 7. Auch dieses Problem läßt sich durch Verwendung von 16-Bit-Zahlen lösen. Eine kleine Trainingsaufgabe für Sie!
Man kann also sagen: Immer dann, wenn bei 8-Bit-Rechnungen der mittels Zweierkomplementzahlen darstellbare Bereich (127 bis —128) über- oder unterschritten wird, fuhrwerkt man im Vorzeichen-Bit herum und verfälscht das Ergebnis. Dann leuchtet wie eine rote Ampel die Überlauf(V)-Flagge auf und sagt uns, daß wir besser in diesen Fällen mit 16-Bit-Zahlen arbeiten sollten.
Nun noch zum Ignorieren des Carry-Bits, das ich weiter oben erwähnt habe. Bei allen 8-Bit-Rechenoperationen mit Zweierkomplementzahlen kann das Carry-Bit vernachlässigt werden. Zwei Beispiele sollen das wieder illustrieren. Wir addieren +4 und —2:
| +4 | 0000 0100 | ||
| —2 | 1111 1110 | ||
| + | + | ||
| —6 | (1) 1111 1000 |
Das Carry-Bit wird außer acht gelassen. Anderes Beispiel: Wir addieren zwei negative Zahlen, —4 und —6:
| —4 | 1111 1010 | ||
| —2 | 1111 1110 | ||
| + | + | ||
| —6 | (1) 1111 1000 |
Auch hier kann man (sogar: muß man) das Carry-Bit vernachlässigen. Beide Ergebnisse sind richtig.
Nun wissen Sie alles über die Art, wie unser Rechner mit ganzen Zahlen arbeitet. Probieren Sie mal ein paar Aufgaben aus zur Übung.
Wir verlassen jetzt den Zahlendschungel und widmen uns der Praxis.
Der Computer rechnet: ADC, CLC
ADC ist der erste Arithmetik-Befehl des 6502 (und natürlich auch des 6510), den wir kennenlernen. Er bedeutet »add with carry«, also »addiere mit Carry-Bit«. An einem 8-Bit-Beispiel wollen wir uns das mal ansehen. ZAHL1 und ZAHL2 sollen addiert werden. Beide sollen positive 8-Bit-Zahlen sein, die so klein sind, daß kein Überlauf zu erwarten ist. Die ZAHL1 wird in den Akku gegeben:
LDA #ZAHL1
Wenn wir nun den Befehl
ADC #ZAHL2
folgen lassen, sorgt die ALU (arithmetisch-logische Einheit, siehe Folge 1) dafür, daß beide Zahlen addiert werden und das Ergebnis im Akku erscheint. ZAHL1 ist dann vom Ergebnis überschrieben worden. An sich ist damit alles erledigt. Weil wir aber häufig wissen wollen, was denn nun bei der Addition herausgekommen ist, speichern wir den Akku-Inhalt noch irgendwo ab mittels »STA Speicherstelle«. Außerdem war da ja noch die Sache mit dem Carry-Bit. Wir haben oben festgestellt, daß bei einer 8-Bit-Addition kein Carry-Bit berücksichtigt werden soll. Nun gibt es aber eine ganze Menge von Vorgängen in einem Assembler-Programm, die das Carry-Bit beeinflussen. Man kann eigentlich vor einer Addition nie ganz sicher sein, ob es denn nun 1 oder 0 ist. Weil jedoch ADC auch das Carry-Bit mitaddiert, sollte man dafür sorgen, daß es vor dem Zusammenzählen wirklich gelöscht ist. Dazu gibt es den Befehl CLC was die Abkürzung für »clear carry«, also »lösche Carry-Bit« ist. Sei ZAHL1 = 12 und ZAHL2 = 7, dann würde unser vollständiges 8-Bit-Additions-Progrämmchen also lauten
| 1200 | CLC | |
| 1201 | LDA | #$0C |
| 1203 | ADC | #$07 |
| 1205 | STA | 1500 |
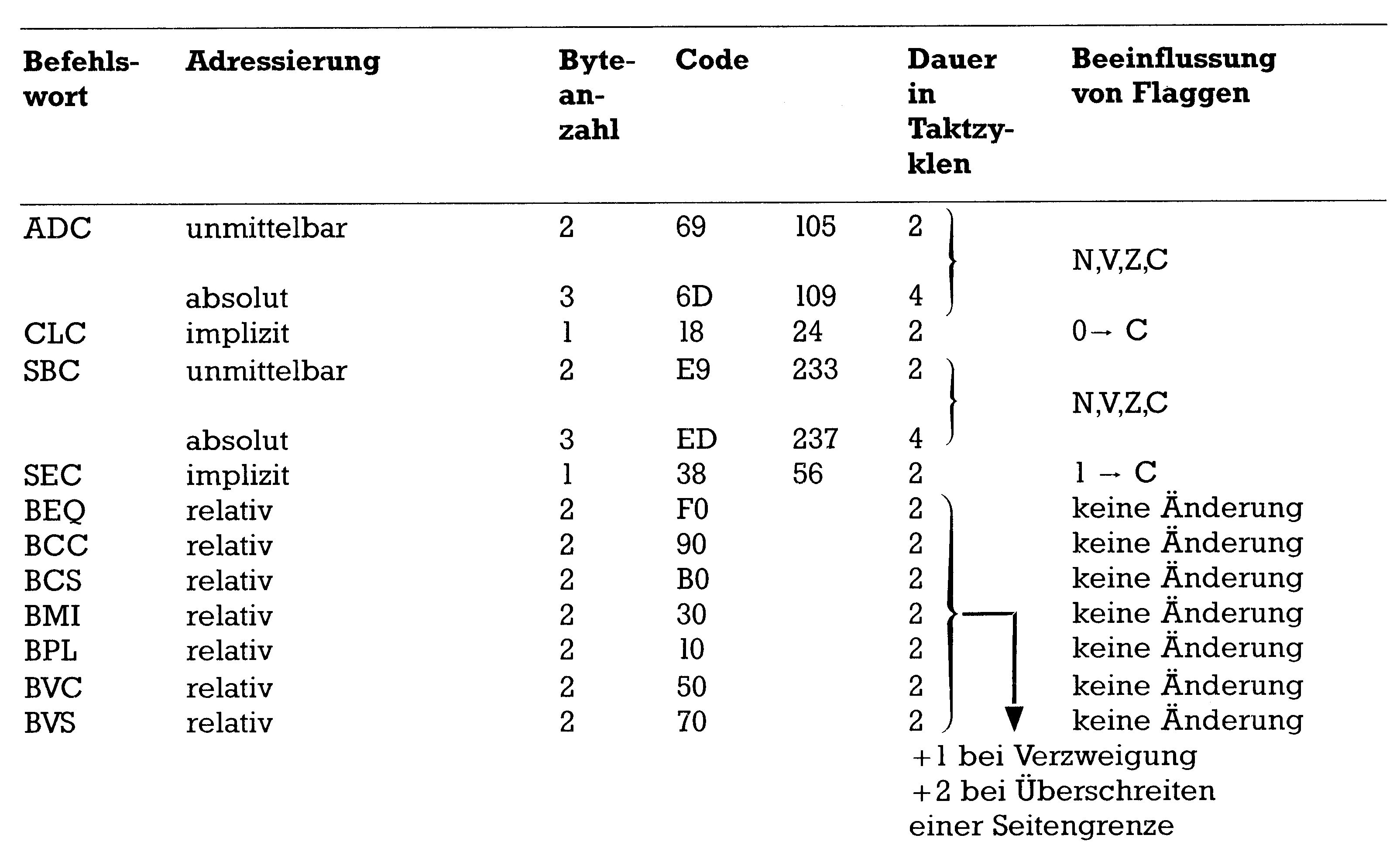
Sehen wir mal davon ab, daß dieses Programm natürlich unsinnig ist (das kann man ja im Kopf schneller rechnen!), dann erkennen wir: CLC ist ein 1-Byte-Befehl mit impliziter Adressierung, welcher sich nur auf die C-Flagge (also das Carry-Bit) auswirkt. ADC ist in der hier verwendeten Form ein 2-Byte-Befehl und liegt in der »unmittelbar« genannten Adressierung vor. Wie wir oben gesehen haben, kann ADC — je nach Art der Rechnung — auf einige Flaggen wirken: Da wären zunächst natürlich die V-Flagge und die C-Flagge. Dann aber kann beim Auftreten eines gesetzten Bit 7 auch die N-Flagge und beim Überschreiten von $FF eventuell auch die Z-Flagge verändert werden.
Viel interessanter wird unser Mini-Programm schon, wenn man anstelle von
| 1201 | LDA | #$0C |
| 1201 | LDA | 1400 |
Weil das ein 3-Byte-Befehl ist, verschiebt sich natürlich der Rest des Programmes um 1 Byte. So kann man immerhin schon zu unterschiedlichen Inhalten von 1400 den gleichen Betrag addieren.
Am interessantesten allerdings ist die Tatsache, daß auch ADC absolut adressierbar ist. Wir können so zum Beispiel den Inhalt der Speicherzelle 1300 zum Inhalt der Zeile 1400 hinzuzählen und dann das Ergebnis in 1500 ablegen:
| 1200 | CLC | |
| 1201 | LDA | 1400 |
| 1204 | ADC | 1300 |
| 1207 | STA | 1500 |
Hier ist der ADC-Befehl dann 3 Bytes lang geworden.
Vergessen Sie bitte nicht — das gilt vor allem für die nachfolgenden Rechenoperationen — dann, wenn die Wahrscheinlichkeit besteht, daß der Dezimal-Modus eingeschaltet ist (also die D-Flagge auf 1 gesetzt ist), noch den Befehl CLD vor solche Programme zu stellen.
Solche 8-Bit-Rechnungen kommen recht häufig vor: Wenn man in Schleifen nicht mit mehrfach wiederholten INX (beziehungsweise INY oder INC, DEX, DEY oder DEC) arbeiten will, addiert man eben immer die Sprungweite mittels ADC hinzu. Der Akku kann nicht als Zähler dienen, denn es gibt für ihn keinen Befehl, der dem INX und so weiter vergleichbar wäre, weswegen man ihn — sollte es nötig sein — mittels ADC hochzählt.
Häufiger und in der Praxis bedeutender sind 16-Bit-Rechnungen. Wie Sie sicher noch aus den vorangegangenen Folgen wissen, teilt man so eine 16-Bit-Zahl auf in zwei Bytes (das LSB und das MSB). Nehmem wir für unser nachfolgendes Beispiel wieder an, daß die Zahlen so gebaut sind, daß kein Überlauf zu befürchten ist. ZAHL1 hätten wir vorher in die Speicherstellen 1300 (LSB) und 1301 (MSB) gepackt, ZAHL2 liegt in den Zellen 1400 (LSB) und 1401 (MSB). Zunächst wieder die Vorbereitungsmaßnahmen:
| 1200 | CLD |
| 1201 | CLC |
Dabei ist CLD nicht immer nötig, wie schon gesagt. Nun addieren wir zuerst die LSBs:
| 1202 | LDA | 1300 |
| 1205 | ADC | 1400 |
| 1208 | STA | 1500 |
Ein Überlauf kann hier nicht stattgefunden haben, denn das Vorzeichenbit ist ja im MSB als Bit 15 enthalten, wohl aber kann ein Übertrag stattgefunden haben: Das Ergebnis könnte größer als 255 ($FF) gewesen sein. War das der Fall, dann ist jetzt eine 1 im Carry-Bit. Wir addieren nun die MSBs:
| 120B | LDA | 1301 |
| 120E | ADC | 1401 |
| 1211 | STA | 1501 |
Egal, was im Carry-Bit stand: Es wurde jetzt hinzuaddiert. Das Ergebnis unserer Rechnung steht nun in 1500 (LSB) und 1501 (MSB). Sehen wir uns das ganze nochmal am Zahlenbeispiel an. Wir addieren die Zahlen 2176 (binär: 0000 1000 1000 0000) und 1009 (binär: 0000 0011 1111 0001). Die Speicherinhalte sind dann:
| 1300 | 1000 0000 | LSB Zahl1 |
| 1301 | 0000 1000 | MSB |
| 1400 | 1111 0001 | LSB Zahl2 |
| 1401 | 0000 0011 | MSB |
Jetzt addieren wir die LSBs:
| 1300 | 1000 0000 |
| 1400 | 1111 0001 |
| Carry | 0 |
| 1500 | 0111 0001 |
| Carry: | 1 |
Nun folgt der zweite Teil der Addition mit den MSBs:
| 1301 | 0000 1000 |
| 1401 | 0000 0011 |
| Carry | 1 |
| 1501 | 0000 1100 |
Damit steht nun das Ergebnis 3185 (binär 0000 1100 0111 0001) säuberlich aufgeteilt in LSB (Speicher 1500) und MSB (Speicher 1501) fest. Das Carry-Bit steht auch nach vollendeter Rechnung noch auf 1, so daß es vor erneuter Addition wieder mit CLC zu löschen ist.
Damit wäre alles über die Addition berichtet. Wie immer in Programmiererkreisen die Empfehlung: Üben, üben,….
Wir wenden uns jetzt der gegenläufigen Operation zu: Der Subtraktion.
Noch mehr Rechnen: SBC, SEC
Daß das Abziehen von Zahlen im Computer durch das Hinzuzählen des Zweierkomplementes geschieht, haben wir mit viel Gehirnschmalzverbrauch schon in vorangegangenen Abschnitten erfahren. Nun sollen Sie die dazu nötigen Befehlsworte des Assemblers kennenlernen. Zunächst einmal ist da SBC. Das heißt »subtract with carry« oder auf deutsch etwa »ziehe unter Berücksichtigung des Carry-Bits ab«. Ebenso wie bei der Addition mit ADC, wirkt das Argument des SBC-Befehls auf den Akku-Inhalt ein — wobei das Ergebnis im Akku landet, diesen also überschreibt. Komplizierter ist hier die Verwendung des Carry-Bits, worauf wir aber nicht detailliert eingehen wollen. (Wen es interessiert: Nachlesen in L.A. Leventhal, »6502 Programmieren in Assembler«, 3. Auflage, München 1983, Seite 3-100). Für uns soll einfach die nicht ganz korrekte Analogie zum »Borgen« bei der Subtraktion ausreichen. Für den Fall, daß ein solches Borgen eintreten muß, sollte auch das dazu nötige Carry-Bit vorhanden sein (also auf 1 gesetzt sein). Wie Sie sicherlich schon erraten haben, heißt SEC »set carry«, also »setze das Carry-Bit« (auf 1).
Merke: Vor einer Addition immer Löschen des Carry-Bits mit CLC, vor einer Subtraktion immer Setzen des Carry-Bits mit SEC!
Zwei Beispiele für die Subtraktion sollen das bisher gesagte erläutern: Zunächst eine 8-Bit-Subtraktion von ZAHL1 (in Speicherzellle 1300) minus ZAHL2 (in Zelle 1400). Ds Ergebnis wird nach 1500 geschrieben:
| 1200 | CLD | |
| 1201 | SEC | |
| 1202 | LDA | 1300 |
| 1205 | SBC | 1400 |
| 1208 | STA | 1500 |
SBC kann — wie hier — absolut adressiert werden, aber auch unmittelbar (also zum Beispiel SBC $40). Der Befehl ist dann im ersten Fall ein 3-, im anderen Fall ein 2-Byte-Befehl. SEC ist ebenso wie vorher schon CLC ein implizit adressierbarer 1-Byte-Befehl.
Das zweite Beispiel ist eine 16-Bit Subtraktion. In den Speichern steht vor dem Aufruf dieser kleinen Routine:
| 1300 | ZAHL1 | LSB |
| 1301 | ZAHL1 | MSB |
| 1400 | ZAHL2 | LSB |
| 1401 | ZAHL2 | MSB |
Das Ergebnis soll nach 1500 (LSB) und 1501 (MSB) gebracht werden:
| 1200 | CLD | |
| 1201 | SEC | |
| 1202 | LDA | 1300 |
| 1205 | SBC | 1400 |
| 1208 | STA | 1500 |
Jetzt sind die beiden LSBs voneinander abgezogen und die Differenz abgespeichert als LSB des Erebnisses.
| 120B | LDA | 1301 |
| 120E | SBC | 1401 |
| 1211 | STA | 1501 |
Damit ist die Aufgabe beendet. Auch die MSBs sind subtrahiert und das MSB des Ergebnisses steht in 1501.
SBC beeinflußt die gleichen Flaggen wie der Befehl ADC.
Ein Programmprojekt
Damit die so kennengelernten Arithmetik-Befehle nicht so trocken auf weiter Flur stehen, wollen wir nun ein Programm entwickeln, aus dem zweierlei zu lernen ist:
- Die Anwendung bisher gelernter Befehle und
- ein häufig angewendetes Verfahren, Assemblerprogramme in Basic-Programme einzubinden.
Besonders dieser 2. Aspekt scheint noch vielen Lesern unklar zu sein (das zeigen mir Zuschriften). Es gibt eine ganze Reihe von Möglichkeiten, zum Einbau von Assembler-Routinen in Basic-Programme; die werden wir alle nach und nach kennenlernen. Von Ihnen sicherlich schon häufig angewendet wurde der SYS-Befehl (zum Beispiel für SYS 58640 und vorherigem POKE214,Zeile und POKE211,Spalte zum Setzen des Cursors an die Stelle Zeile, Spalte). Damit haben Sie ein Maschinenprogramm aufgerufen, das im System unseres Computers schon enthalten ist. 58640 ist die Startadresse des Programmes und man kann diesen SYS-Befehl eigentlich wie eine Art »GOTO Maschinenprogramm-Startadresse« ansehen. Nichts hindert uns also, auf diese Weise eigene Assembler-Programme anzuspringen! Das Problem liegt nun nur noch darin, wie man Parameter, die unsere Maschinenroutine benötigt, übergeben kann. Eine offensichtliche — aber leider auch relativ langsame — Methode ist das POKEn der Werte im LSB/MSB-Format in die Speicherzellen, aus denen sie sich unser ML-Programm dann abholt. Wir wollen dieses Verfahren nun an einem Programmbeispiel verwenden.
Eine arithmetische Reihe werden viele von Ihnen schon kennen. Wenn man A als erstes Glied, D als Differenz und N als die Anzahl der Glieder bezeichnet, dann ist die Summe einer solchen Reihe: S=A+(A+D)+(A+2*D)+…usw….+(A+(N-1)*D)
Ein Beispiel ist die Summe der ersten zehn ganzen Zahlen: S=1+2+3+4+5+6+7+8+9+10
Hier ist A=1, D=1 und N=10. Daß die Summe S im Beispiel 55 ist, kann man schnell berechnen, was aber, wenn wir wesentlich mehr als nur zehn Glieder haben? Es gibt natürlich auch Formeln zur Berechnung von S. Aber eigentlich ist es ganz reizvoll, ohne solche Formeln den Computer die Summe bilden zu lassen. Wir bauen also ein Programm zur Berechnung der Summe der ersten N ganze Zahlen, wobei N frei gewählt werden kann. Das Ergebnis soll eine 16-Bit-Zahl sein, also nicht größer als 32767. Das beschränkt uns bei N auf Werte von 1 bis 255 (Warum, können Sie ja mal mit dem fertigen Programm ausprobieren). N benötigt also nur 1 Byte Speicherplatz und soll in $1300 abrufbar sein. A soll 1 sein ebenso wie D. Für eventuelle Programmänderungen ist es aber sinnvoll, A und D als 16-Bit-Zahlen aufzubewahren und zwar in $1310/1311 (A in LSB/MSB-Format) und in $1320/1321 (D im gleichen Format). Das Ergebnis soll in $1400/1401 zu finden sein. Das Maschinenprogramm legen wir nach $1200.
Zuerst kümmern wir uns um das Basic-Aufrufprogramm:
10 REM **AUFRUF SUMME ARITHMETISCHE REIHE**
20 POKE5120,0:POKE5121,0:REM ERGEBNISSPEICHER AUF NULL
30 PRINTCHR$(147)CHR$(17)CHR$(17)
40 INPUT"ANZAHL DER GLIEDER N=";N
50 IFN<1 OR N>255 THEN PRINT CHR$(17)"1<=N<=255":GOTO40
60 POKE4864,N:REM EINSPEICHERN VON N
70 POKE4880,1:POKE4881,0:POKE4896,1:POKE4897,0:REM EINSPEICHERN VON A UND D
80 SYS4608:REM AUFRUF UNSERES MASCHINENPROGRAMMES
90 M=PEEK(5121):L=PEEK(5120):REM AUSLESEN DES ERGEBNISSES
100 E=256*M+L:PRINTCHR$(17)CHR$(17)
110 PRINT"DIE SUMME DER ERSTEN "N" GANZEN ZAHLEN IST:":PRINTE
120 END
Zu diesem Programm gibt es nur noch zu bemerken, daß die Zahlen bei POKE, PEEK oder SYS die Dezimalwerte unserer oben gewählten Adressen sind.
Nun endlich zum Assemblerprogramm. Sehen Sie sich dazu bitte das Flußdiagramm im Bild 2 an.
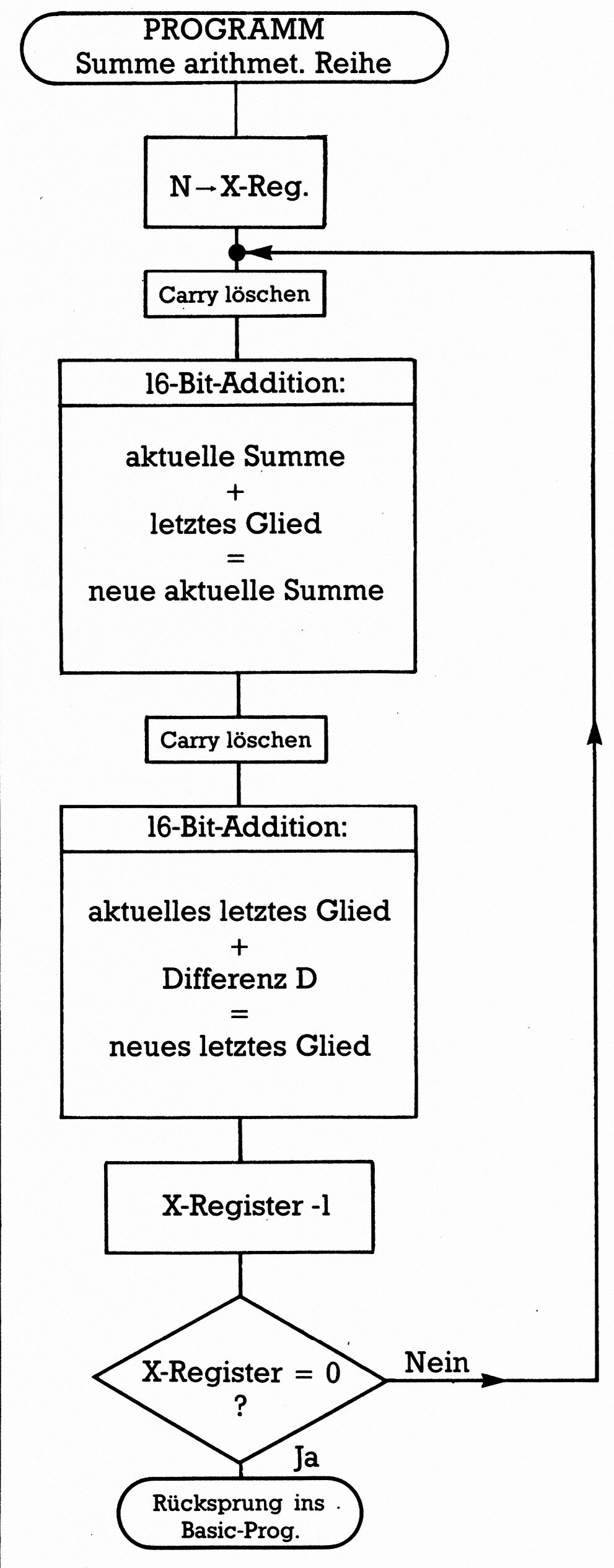
Wir bereiten den Ablauf vor, indem wir aus $1300 die Anzahl der Glieder ins X-Register laden und zur Vorbereitung der Addition das Carry-Bit löschen. Schalten Sie also bitte den SMON ein und tippen Sie A1200 <RETURN>. Es erscheint die Startadresse 1200. Jetzt können Sie Zeile für Zeile das Assembler-Programm eingeben (nach jeder Zeile ein RETURN, das die nächste Zeilennummer erzeugt):
| 1200 | LDX | 1300 |
| 1203 | CLC |
Die nächsten sechs Zeilen summieren jeweils das neueste Glied zur bis dahin erzeugten Summe. Jetzt zu Beginn ist $1400/1401 noch leer und in $1310/1311 steht noch das Anfangsglied A = 1. Später mit Durchlaufen der Schleife, steht in $1400/1401 immer die bis dahin gebildete Summe und in $1310/1311 das letzte Glied der Reihe. Es handelt sich um die oben kennengelernte 16-Bit-Addition:
| 1204 | LDA | 1400 |
| 1207 | ADC | 1310 |
| 120A | STA | 1400 |
Das neue LSB ist berechnet und in $1400 geschrieben.
| 1200 | LDA | 1401 |
| 1210 | ADC | 1311 |
| 1213 | STA | 1401 |
Das war nun noch das neue MSB. Als nächstes berechnen wir das momentan letzte Glied der Reihe durch Addieren von D zum alten letzten Glied. Das entspricht dem Basic-Befehl A=A+D in einer Schleife. Dies ist eine neue 16-Bit-Addition, weshalb wir wieder CLC vorgeben müssen:
| 1216 | CLC | |
| 1217 | LDA | 1310 |
| 121A | ADC | 1320 |
| 121D | STA | 1310 |
Das war wieder das LSB. Nun zum MSB:
| 1220 | LDA | 1311 |
| 1223 | ADC | 1321 |
| 1226 | STA | 1311 |
Wir zählen nun das X-Register um 1 herunter und prüfen, ob es schon Null geworden ist, ob also schon alle N-Glieder summiert worden sind:
| 1229 | DEX | |
| 122A | BNE | 1203 |
Wenn noch nicht alle Glieder berechnet und summiert sind, kehren wir an den Schleifenanfang zurück. Ansonsten springen wir zurück ins Basic-Aufrufprogramm:
| 122C | RTS |
Wenn Sie beide Programme eingetippt haben, dann speichern Sie sie vorsichtshalber ab (das Assemblerprogramm mit dem S-Befehl des SMON). Beim neuen Einladen brauchen Sie den SMON nicht mehr. Nach dem Laden unseres Maschinenprogrammes (mit ,8,1 bei Diskette oder ,1,1 bei Kassette) geben Sie NEW <RETURN> ein, damit die Zeiger vor dem Einladen des Basic-Programmes wieder auf Normalwerte gesetzt werden. Zwischen dem dann eingeladenen Basic-Programm und unserer Assembler-Routine ist genug Platz. Sollten Sie aber irgendwann mal das Basic-Programm vergrößern, schützen Sie bitte unseren Bereich ab $1200.
Unser Assembler-Beispiel ist so aufgebaut, daß auch A und D variabel gehalten sind. Sie müßten dann nur noch Eingabemöglichkeiten im Basic-Programm schaffen und anstelle der Werte 1 oder 0 in Zeile 70 die LSBs und MSBs der von Ihnen eingegebenen Größen A und D einPOKEn. Auf diese Weise sind dann beliebige ganzzahlige, arithmetische Reihen berechenbar, wie zum Beispiel S = 7+10+13+16+… und so weiter. Das überlasse ich Ihrer Basic-Programmierfertigkeit. Nur eines noch: Sie müssen darauf achten, daß die Summe S nicht größer als 32767 wird. Ihrer Phantasie sind — wie immer in diesem Metier — keine Grenzen gesetzt. Sie könnten sich ja mal überlegen, wie man größere Summen zulassen kann (wer sagt denn, daß wir Zahlen immer nur in 2 Bytes darstellen dürfen?). Oder Sie könnten sich überlegen, welches eindeutige Merkmal auftritt, sobald der Maximalwert überschritten wird (ein Tip: Lesen Sie doch mal den Abschnitt über die V-Flagge nach).
Die Branch-Befehle
Der 6502 (und auch der damit identische 6510) kennt acht bedingte Verzweigungen, von denen wir bisher BNE schon verwendet haben. Alle diese Branch-Befehle (von branch = verzweigen) prüfen Flaggen des Statusregisters.
BNE und BEQ beziehen sich auf die Z-Flagge, die anzeigt,ob im Verlauf der letzten Operation eine Null aufgetreten ist. Ist das der Fall, steht in der Z-Flagge eine 1. BNE verzweigt zur angegebenen Adresse, wenn in der Z-Flagge eine 0 enthalten ist. BEQ (branch if equal zero = verzweige, wenn gleich Null) tut das dann, wenn die Z-Flagge auf 1 gesetzt ist. Da muß man etwas aufpassen, daß man sich nicht vertut!
BCC und BCS haben ihre Aufmerksamkeit auf die C-Flagge, also das Carry-Bit gerichtet. BCC kommt vom englischen »branch if carry clear«, was heißt: »verzweige, wenn das Carry-Bit gelöscht ist«. Ein gesetztes Carry-Bit (also Inhalt = 1) veranlaßt BCS (»branch if carry set« = verzweige, wenn das Carry-Bit gesetzt ist) zum Sprung an die angegebene Adresse.
Diese vier bedingten Verzweigungen sind an sich die bedeutsamsten und am häufigsten verwendeten Branch-Befehle. Man kann wohl getrost sagen, daß über 90% der von Programmierern verwendeten bedingten Sprünge, damit absolviert werden. R. Mansfield warnt sogar ausdrücklich in seinem Buch »Machine language for beginners«, einem in den USA sehr verbreitetem Werk, vor der Verwendung der Befehle BPL und BMI!
Dafür liegt absolut kein einsehbarer Grund vor. Viele programmtechnischen Aufgabenstellungen lassen sich elegant und leicht mit BPL, BMI, BVS und BVC lösen. Man muß nur wissen, wie sie funktionieren und — da liegt vermutlich der Hund begraben — man muß auch die Art kennen, wie Zahlen vom Computer behandelt werden. Genau das aber wissen wir und deswegen sollten wir diese Kenntnis für uns auch nutzen. Also ohne Scheu heran an die verfehmten Befehle!
BMI und BPL (branch on minus = verzweige, wenn negativ und branch on plus = verzweige, wenn positiv) hängen mit der Negativ-Flagge N zusammen. Das Rätsel dieser Flagge konnte in den vorangegangenen Folgen gelöst werden: Immer dann, wenn bei einer Operation eine Zahl auftrat, deren Bit 7 eine 1 war, wurde die N-Flagge auf 1 gesetzt. Wir wissen jetzt, daß dieses Bit bei 8-Bit-Zahlen das Vorzeichenbit ist. Bit 7 sagte uns bei einer 1, daß eine negative Zahl im Zweierkomplement-Format vorliegt oder aber überhaupt ein Speicherzelleninhalt vorhanden ist, der größer als 0111 1111 = 127 ist. BMI führt zum Sprung in diesem Fall, weil die N-Flagge auf 1 steht. Andernfalls führt BPL zur Verzweigung.
Ebenso einfach sind BVS und BVC zu erklären: Sie beziehen sich auf die V-Flagge, unsere rote Ampel, die Überlauf bei Rechenoperationen anzeigt. Kann es was bequemeres geben zur Behandlung solcher Fehlrechnungen als ein »branch on overflow set« = »verzweige, falls die Überlauf-Flagge gesetzt (= 1) ist« mit BVS? Oder anders herum bei BVC »branch on overflow clear« = »verzweige bei freier Überlauf-Flagge«. Wenn man — wie Sie jetzt nach dieser Folge — weiß, unter welchen Umständen diese V-Flagge auf 1 gesetzt wird, sollte man ohne Skrupel BVS und BVC ausgiebig benutzen. Man könnte damit zum Beispiel programmieren, daß die Rechengenauigkeit automatisch von 16-Bit auf 24- oder 32- (oder wie es gerade beliebt) Bit gesteigert wird, ohne daß man sich bei jeder Programmaufgabe Gedanken über das größtmögliche Ergebnis machen muß. Dazu aber ein andermal mehr.
Alle hier vorgestellten Branch-Befehle sind ebenso wie BNE 2-Byte-Befehle, was an der speziellen Art der Adressierung liegt: Der relativen Adressierung.
Eigentlich hatte ich Ihnen ja versprochen, diese relative Adressierung zusammen mit den Branch-Befehlen zu erklären. Ich werde ihr aber lieber einen eigenen Abschnitt widmen, weil’s zum genauen Verständnis doch etwas mehr an Aufwand braucht. Die nächste Folge fängt dann damit an, abgemacht?
Wie die anderen Folgen auch, soll auch diese hier noch mit einer Tabelle enden, in der die neu gelernten Befehle mit Zubehör gezeigt sind.
(Heimo Ponnath/gk)