Effektives Programmieren (5): Sortieren in Basic — Teil 2

Einfache Sortieralgorithmen sind leider auch die langsamsten. Dennoch lassen sie sich durch einige kleinere Änderungen noch erheblich verbessern, so zum Beispiel Bubblesort. Wesentlich komplizierter ist da schon Shellsort, dafür aber auch schneller. Wir zeigen Ihnen, wie es funktioniert.

In der letzten Folge beschäftigten wir uns mit straight insertion und mit Bubblesort, zwei sehr einfachen Sortieralgorithmen. Diesmal wollen wir das Niveau schon ein wenig anheben, um uns dem eigentlichen Ziel unseres Kurses langsam zu nähern. Letztendlich geht es uns nur darum, eine möglichst schnelle und effektive Sortiermethode für praktische Anwendungen zu suchen. Fangen wir deshalb gleich einmal mit der Verbesserung eines Sortieralgorithmus an, der letztes Mal besprochen wurde.

Haben Sie sich mit Bubblesort schon intensiver beschäftigt? Wenn ja, werden Sie auch ganz bestimmt dessen Schwächen ausfindig gemacht haben. Wir erinnern uns: Bubblesort fängt am Anfang eines Variablenfeldes an und vergleicht die beiden ersten Variablen. Steht die größere der beiden weiter vorne, so werden die Variablen vertauscht. Jetzt vergleicht er die zweite mit der dritten Variablen des Arrays und setzt dieses Vergleichen und Austauschen solange fort, bis das gesamte Feld durchgearbeitet ist und die größte Variable jetzt am Ende des Arrays steht. Als nächstes wird das Variablenfeld um die letzte Variable vermindert, so daß jetzt der zweitgrößte String auf die gleiche Art und Weise »nach unten« befördert wird. Diese Vorgänge wiederholen sich so lange, bis nur noch eine Variable übrigbleibt, die jetzt die kleinste ist.

Bubblesort optimiert

Nun aber zu den Schwächen von Bubblesort. Ist Ihnen beim Ausprobieren des Programms aus der letzten Folge vielleicht aufgefallen, daß Bubblesort sehr »stur« arbeitet? Es kann nämlich ohne weiteres passieren, daß ein Feld bereits nach dem dritten Durchgang vollständig sortiert vorliegt. Dies wird von Bubblesort jedoch nicht erkannt. Der Computer »sortiert« weiter, bis alle Durchläufe erledigt sind.

Dieses Problem können wir ganz einfach lösen, indem wir ein Flag einsetzen, das uns anzeigt, ob im letzten Durchgang noch eine Vertauschung stattgefunden hat. Wurde kein Tausch mehr vorgenommen, so wird der Sortiervorgang beendet. Dieses Flag ist schon eine ziemliche Verbesserung gegenüber der Rohversion, aber wir wollen uns damit noch nicht zufriedengeben.

Es kann beim Sortieren auch durchaus der Fall eintreten, daß im letzten Durchlauf nur noch beispielsweise drei Vertauschungen im ersten Drittel des Feldes stattgefunden haben. Die letzten beiden Drittel des Feldes sind also bereits sortiert.

Damit Bubblesort auch diesen Fall erkennt, wird eine zweite zusätzliche Variable eingeführt, die die Position der jeweils letzten Vertauschung eines Durchlaufes beinhaltet. Es wird nun im weiteren Verlauf immer nur bis zu dieser Position gearbeitet, da der Rest des Feldes bereits sortiert vorliegen muß.

Mit diesen beiden Verbesserungen wollen wir es aber bereits gut sein lassen (Listing 1, Bild 1). Der neue Bubblesort-Algorithmus arbeitet besonders bei schon teilsortierten Feldern ziemlich effizient; ist der »alten« Version jedoch bei total vermischten Feldern infolge der zusätzlichen (Zeit verbrauchenden) »Erweiterungen« unterlegen.

Bubblesort soll uns nun nicht weiter beschäftigen, denn trotz seines wohlklingenden Namens ist er so ziemlich der langsamste Algorithmus, den es gibt.

An dieser Stelle gleich einmal ein paar Bemerkungen zur Zeitmessung: Die jetzt vorgestellten Algorithmen, die Sie jeweils als Listings abgedruckt finden, sind in der Form zur Zeitmessung natürlich nicht geeignet. Das liegt daran, daß die Programme so aufgebaut sind, daß Sie den Algorithmus leicht nachvollziehen können, was natürlich auf Kosten der Geschwindigkeit geht und die Ergebnisse verfälschen würde.

Im abschließenden Artikel über die Sortiermethoden werden wir die einzelnen Programme jedoch auch unter dem Aspekt »Zeit« einander gegenüberstellen. Hier werden wir auch auf das Problem der Garbage Collection eingehen, die uns beim Sortieren von größeren Feldern, je nach Algorithmus, ganz schön in Schwierigkeiten bringen kann, wenn es um eine Zeitmessung geht.

Ein weiteres Problem bei der Zeitmessung ist aber auch die Eigenart der einzelnen Sortiermethoden. Ich erwähnte schon in der letzten Folge, daß es natürliche und unnatürliche Algorithmen gibt, wobei die natürlichen dann am schnellsten arbeiten, wenn das Feld schon sortiert vorliegt.

Für die Mathematiker unter Ihnen ist jedem Sortieralgorithmus eine kleine Formel zur Berechnung der mittleren (!) Sortierzeit beigefügt. Diese Formel dient nur der Gesamtbetrachtung und zeigt jeweils, warum die einen Algorithmen so langsam und andere wesentlich schneller sind.

straight selection

Nun aber zu einer neuen Sortiermethode. Es handelt sich hierbei um ein Sortieren durch direktes Auswählen, was durch einen englischen Ausdruck wieder passend beschrieben wird: straight selection.

Auch straight selection ist ein relativ einfacher Algorithmus, dessen Funktionsweise wir uns gleich etwas näher betrachten wollen (Bild 2).

Im ersten Durchgang sucht der Computer nach dem größten Element im Feld. Wird dieses gefunden, so erfolgt eine Vertauschung zwischen diesem Element und dem allerletzten des Feldes, da die größte Variable logischerweise am Schluß stehen muß. Jetzt wird die Länge des Feldes durch Wegnahme des letzten Elements um 1 vermindert. Danach wird in diesem »Rest-Array« wiederum nach dem größten Element gesucht und dieses ebenfalls mit dem letzten Element (das jetzt das vorletzte des Gesamtfeldes ist) vertauscht. Dieser Vorgang wiederholt sich so lange, bis die Länge des Restfeldes 1 ist und wir an erster Position zwangsläufig das kleinste Element erhalten.

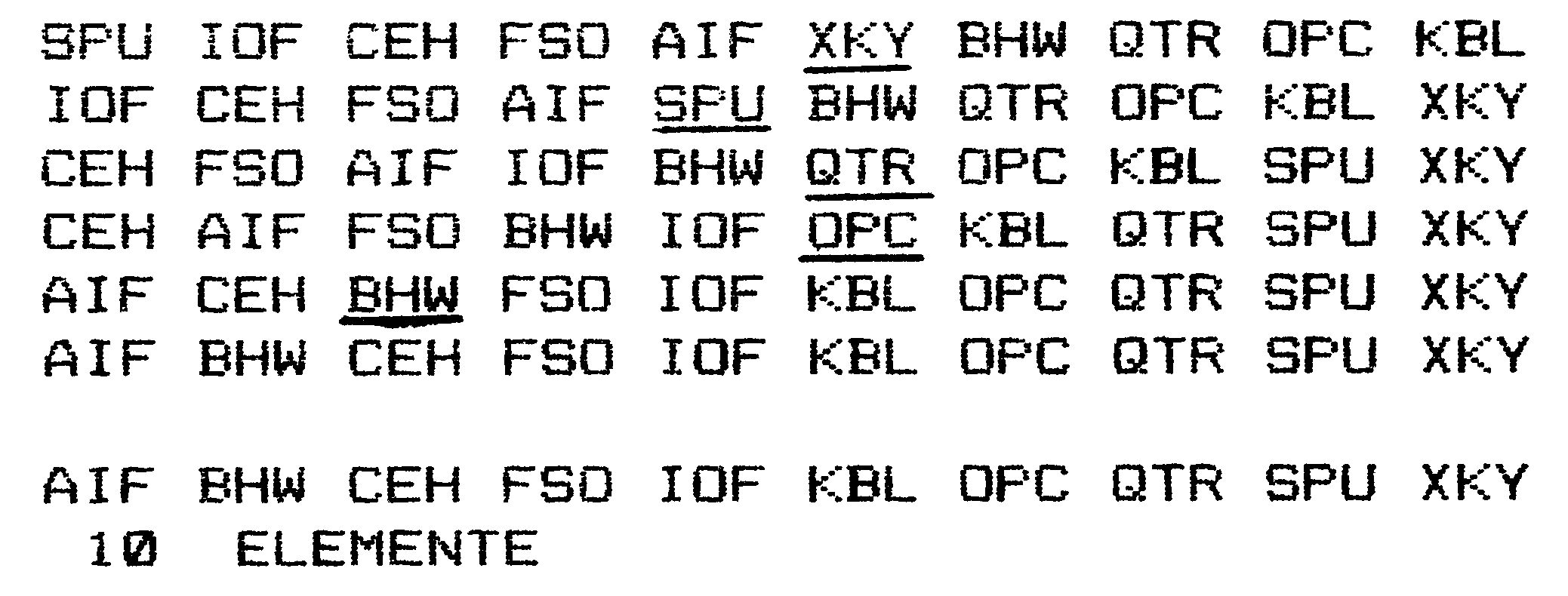
In Bild 3 können Sie die Arbeitsweise von straight selection an einem praktischen Beispiel nachvollziehen, wobei immer jene Elemente unterstrichen sind, die im nächsten Schritt einsortiert werden.

Natürlich funktioniert straight selection auch andersherum, das heißt Sie können jeweils nach dem kleinsten Element suchen und dieses dann mit dem an erster Stelle stehenden Element vertauschen.

Um Ihnen auch die Zeitverhältnisse zu beschreiben, oder um Ihren mathematischen Geist zu beflügeln (wie Sie wollen), seien an dieser Stelle einmal wieder zwei Formeln über straight selection aufgestellt.

Für seine Arbeit benötigt straight selection eine mittlere Anzahl von Vergleichen, die in etwa durch die folgende Formel angenähert werden, wenn wir davon ausgehen, daß a die Anzahl der zu sortierenden Elemente enthält:

$$\text{Anzahl Vergleiche: }\mathrm{\frac{a ^ 2 - a}{2}}$$

Für die Anzahl der Bewegungen innerhalb der Arrays gilt folgende Beschreibung:

$$\text{Anzahl Bewegungen: }\mathrm{a - 1}$$

Mit straight selection haben wir unter anderem gleich das erste Beispiel für einen unnatürlichen Sortieralgorithmus. Wenn wir ein Feld bearbeiten wollen, das schon sortiert vorliegt, so braucht unser Programm sehr lange, um das größte Element ausfindig zu machen, da wir von vorne mit dem Suchen beginnen. Bearbeiten Sie also meistens schon teilsortierte Felder, so ist es ratsam, mit der Suche des größten Elements von hinten zu beginnen. Die Umstellung des Programms in Listing 2 dürfte Ihnen keine Schwierigkeiten bereiten, da lediglich die Suchschleife umzudrehen und mit STEP1 zu versehen ist.

So, das wäre auch schon alles, was zu straight selection zu sagen ist. Wie Sie sehen, ist das immer noch ein sehr einfacher Algorithmus, der in etwa mit straight insertion gleichzusetzen ist, was die Effektivität betrifft. Diese Gleichsetzung gilt aber natürlich nur für zufallsbesetzte Felder.

Shellsort

Der nächste Sortieralgorithmus trägt den Namen seines Erfinders (D.L.Shell) und wurde 1959 entwickelt. Es handelt sich hierbei schon um einen komplizierteren Algorithmus, den wir deshalb sehr ausführlich besprechen wollen (Bild 4). Shellsort ist ein Sortieren durch direktes Einfügen und gehört damit der gleichen »Familie« wie straight insertion an.

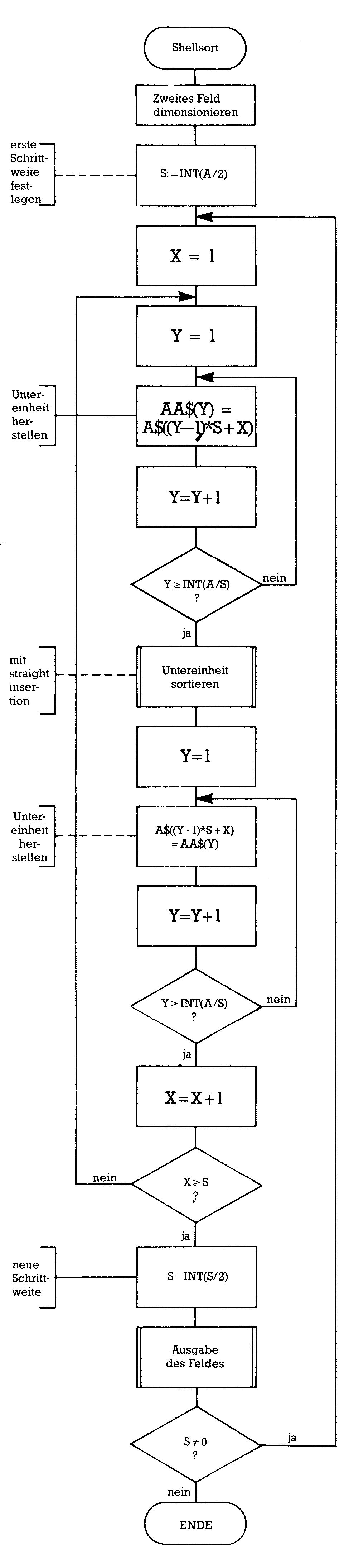
Durch entsprechende Berechnungen hatte Shell herausgefunden, daß sich Sortiervorgänge beschleunigen lassen, wenn nicht nur benachbarte Elemente miteinander verglichen werden, sondern auch weiter voneinander entfernte. Wir vergleichen also beispielsweise nicht mehr das erste Element mit dem zweiten, sondern vielmehr das erste mit dem fünften.

Durch diese Methode erreicht man eine gewisse »Grobsortierung«, die sich jedoch gleichmäßig über das gesamte Feld verteilt. Das so neu entstandene Variablenfeld wird wiederum sortiert, wobei jetzt aber das erste mit dem dritten Element verglichen wird. Die Sortierung wird also durch abnehmende Abstände zunehmend »feiner«, bis beim Abstand 1 die letzte, absolute Sortierung erfolgt.

Unklar? Keine Angst, wir werden das gleich einmal an einem praktischen Beispiel erläutern.

Sehen Sie sich Bild 5 an. Hier haben wir ein zufällig geordnetes Feld mit zehn Elementen. Als ersten Abstandswert nimmt Shellsort üblicherweise a/2, also die Hälfte der Gesamtanzahl der Elemente. In unserem Fall ist das 5.

Aus diesem umsortierten Feld holen wir jetzt alle Zahlen zu Untereinheiten zusammen, die den Abstand (besser: die Schrittweite) 5 haben. In Bild 5 sehen Sie diese Zusammenstellungen: Es wurde also jeweils das 1. mit dem 6., das 2. mit dem 7., das 3. mit dem 8., das 4. mit dem 9. und das 5. mit dem 10. Element zu einer Einheit zusammengefaßt.

Da die Schrittweite 5 ist, kann jede Untereinheit verständlicherweise nur zwei Elemente enthalten. Nun, was sollen wir jetzt mit diesen Untereinheiten machen?

Diese werden sortiert, und zwar verwenden wir dabei einen einfachen und unkomplizierten Sortieralgorithmus, wie zum Beispiel straight insertion.

Wir sortieren also die erste Untereinheit, aus (9,7) wird (7,9). Jetzt schreiben wir diese Untereinheit wieder an die gleiche Position in unser Feld zurück, wobei jedoch die 7 dort steht, wo vorher die 9 stand und umgekehrt. Dann sortieren wir die zweite Untereinheit und schreiben sie ebenso zurück. Das geschieht so lange, bis alle Untereinheiten abgearbeitet worden sind und wir wieder ein vollständiges Array erhalten.

Jetzt wird die Schrittweite 5 halbiert und die Nachkommastelle des Ergebnisses abgeschnitten. Wir erhalten als neue Schrittweite 2. Wieder legen wir uns Untereinheiten an, wobei wir jedoch nur mehr zwei Untereinheiten zu je fünf Elementen bekommen. Wichtig für die Programmentwicklung ist an dieser Stelle die Entdeckung, daß die Anzahl der Untereinheiten grundsätzlich der Schrittweite entspricht.

Auch hier wird mit den Untereinheiten wieder verfahren, wie oben. Sie werden sortiert und wieder in das ursprüngliche Array zurückgeschrieben. Das Ergebnis des letzten Durchlaufes können Sie wieder in Bild 5 ablesen. Der nächste Durchlauf ist schon der letzte; hier ist die Schrittweite nunmehr 1 und es erfolgt eine Schlußsortierung des gesamten Feldes.

Daß Shellsort so schnell ist, obwohl er einige vollständige Sortierläufe als Unterprogramme verwendet, liegt daran, daß das Sortierunterprogramm jeweils ziemlich optimierte Einheiten zur Bearbeitung bekommt. Auch beim letzten Durchgang, wo ja nochmals das gesamte Feld durchsortiert wird, sind die Elemente schon so angeordnet, daß eine Sortierung ohne viele Bewegungen möglich ist. Listing 3 enthält die Shellsortroutine, wobei als Unterprogramm ab Zeile 20 000 straight insertion verwendet wird. Sie können einmal verschiedene Algorithmen in Shellsort verwenden; vielleicht finden Sie eine optimale Zusammenstellung? Das Unterprogramm bearbeitet das Array AA$(x) und erwartet die Anzahl der Elemente in AA.

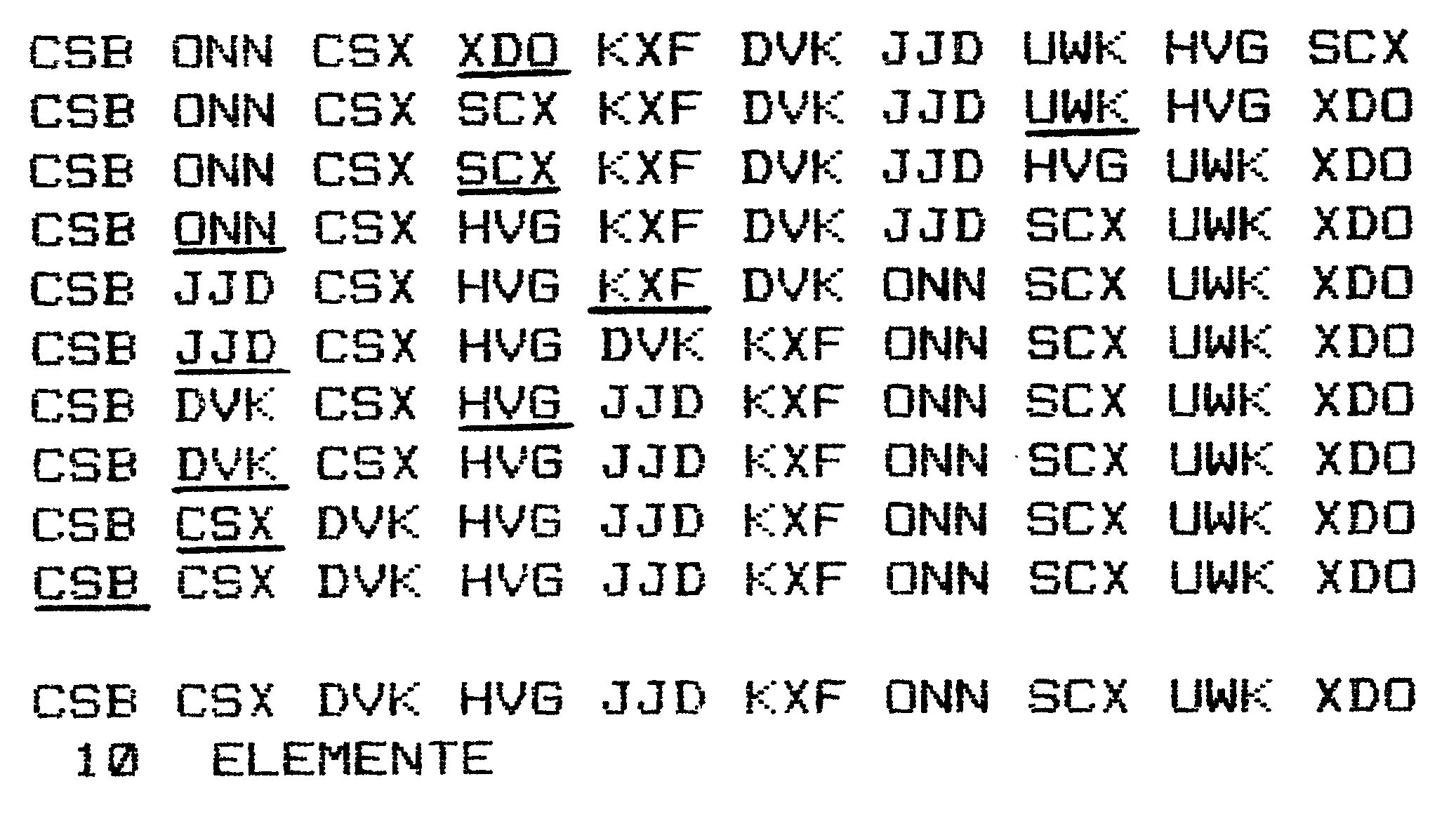
Wenn Sie sich einmal den Beispielausdruck zu Shellsort betrachten (Bild 6), so werden Sie feststellen, daß dieser Algorithmus nur mehr drei Durchgänge für zehn Elemente benötigt. Diese Zahl läßt auf ein gutes Ergebnis hoffen. In der Tat haben wir mit Shellsort schon ein sehr gutes Sortierprogramm, das vielen praktischen Anwendungen gewachsen sein dürfte. Gegenüber der vorher besprochenen Sortieralgorithmen arbeitet Shellsort um einiges schneller, was besonders bei größeren Feldern angenehm auffällt. Für die Schrittweite können übrigens auch andere abfallende Reihen verwendet werden, die mit 1 aufhören. Es hat sich nämlich gezeigt, daß die Wahl der richtigen Reihe entscheidend zur Geschwindigkeit von Shellsort beiträgt.

Wollen wir zu Shellsort eine mathematische Berechnung liefern, wird’s schwierig. Dieser Algorithmus ist bereits dermaßen komplex, daß eine Berechnung fast unmöglich wird. Es kann an dieser Stelle nur eine Aussage über die mittlere Sortierzeit gemacht werden, die sich in etwa im Bereich um a^1.2 bewegt, wobei a wiederum die Anzahl der zu sortierenden Elemente darstellt.

So, mit Shellsort haben wir uns nun endgültig von den einfachen Sortieralgorithmen losgesagt. Wie Sie sehen, kann eine höhere Komplexität der Programme und ein damit verbundener größerer Zeitbedarf, ohne weiteres die Nachteile von einfacheren Programmen aufwiegen. Aber auch hier kommt es natürlich auf die Art der Aufgabenstellung an. Shellsort verträgt zum Beispiel keine umgekehrt sortierten Arrays. Hier wird auch dieser schnelle Sortieralgorithmus langsam.

In der nächsten Folge wollen wir uns ausschließlich mit einem einzigen Sortierprogramm beschäftigen. Es handelt sich um Heapsort. Dieser Algorithmus arbeitet nach dem »Baumprinzip« und ist sehr kompliziert. Aus diesem Grund wollen wir uns ausführlich mit ihm beschäftigen, denn wir haben es dann mit einem der schnellsten Algorithmen zu tun, den es gibt.

10000 rem sortieren durch austauschen
10010 rem verbessert
10020 rem
10030 rem bubblesort 2
10032 rem g ist die letzte position beim
10034 rem vertauschen
10036 rem f zeigt vertauschung an
10040 g=a-1:for x=a-1 to 1 step-1
10050 f=0:for y=1 to g
10060 if a$(y)<=a$(y+1)then 10080
10065 rem austauschen beider elemente
10070 f=y:s$=a$(y):a$(y)=a$(y+1):a$(y+1)=s$
10080 next x
10090 g=f:if f=0 then 10120
10100 gosub 3000: rem ausgabe
10110 next x
10120 rem ende

10000 rem sortieren durch direktes
10010 rem auswaehlen
10020 rem
10030 rem straight selection
10040 for x=a to 2 step-1:x$=""
10050 for y=1 to x
10060 ifa$(y)>x$then x$=a$(y):z=y
10070 next y
10080 s$=a$(x):a$(x)=a$(z):a$(z)=s$
10090 gosub 3000
10100 next x
10110 rem ende

10000 rem sortieren mit abnehmender
10010 rem schrittweite
10020 rem
10030 rem shellsort
10035 dim aa$(a)
10040 s=int(a/2): rem schrittweite
10050 for x=1 to s
10060 for y=1 to int(a/s)
10070 aa$(y)=a$((y-1)*s+x)
10080 next y
10090 aa=y-1:gosub 20000
10100 for y=1 to int(a/s)
10110 a$((y-1)*s+x)=aa$(y)
10120 next y
10130 next x
10140 s=int(s/2)
10150 gosub 3000
10160 if s goto 10050
10170 rem ende
10180 goto 50000
20000 for xx=2 to aa
20010 if aa$(xx)>=aa$(xx-1) then 20080
20020 rem einfuegen des elements
20030 xx$=aa$(xx): for yy=xx-1 to 1 step -1
20040 aa$(yy+1)=aa$(yy)
20050 if xx$<=aa$(yy-1) then 20070
20060 aa$(yy)=xx$: goto 20080
20070 next yy
20080 next xx
20090 return