Dem Klang auf der Spur (Teil 5)
Dieser Teil des Musikkurses ist auch für all jene interessant, die sich nicht ausschließlich für Musik interessieren. Es werden Algorithmen zur Generierung verschiedener Signale vorgestellt.
Dabei wird anhand des Source-Listings des Programms Modulator gezeigt, wie man diese Algorithmen unter zeitkritischen Nebenbedingungen programmieren kann.
Im zweiten Teil dieser Reihe wurde schon erwähnt, daß man jeden Signalverlauf durch eine Folge von Stützwerten beschreiben kann. Da man diese Stützwerte digital codieren kann, wird so die Signalerzeugung und -verarbeitung mit dem Computer möglich. Man muß dabei allerdings mit einer Abtastfrequenz arbeiten, die mindestens doppelt so hoch ist wie die höchste Frequenz, die im verarbeiteten Signal vorkommt. Für Audio-Signale in HiFi-Qulität ist somit eine Abtastfrequenz von mindestens 40 kHz erforderlich. Stellen wir dieser Frequenz einmal die Taktfrequenz von 1 MHz in unserem C 64 gegenüber: Eine Abtastperiode dauert bei 40 kHz 25 µs. Diese Zeit entspricht genau 25 Taktzyklen im C 64. Ein 6510-Maschinenbefehl dauert zwischen zwei und sieben Taktzyklen, das heißt, daß die CPU während einer Abtastperiode gerade vier bis maximal zwölf Befehle abarbeiten kann; zuwenig, um damit schon sinnvoll einen Signalabtastwert weiterzuverarbeiten. Die digitale Verarbeitung von Audiosignalen bleibt also zunächst einmal Hochleistungsrechnern und Spezialprozessoren vorenthalten.
Dreh- und Angelpunkt: Integer-Arithmetik
Wenn man sich aber wie bei dem in der letzten Folge vorgestellten Programm Modulator auf eine Abtastfrequenz von 60 Hz beschränkt, dann sieht die Sache schon sehr viel günstiger aus. Während einer Abtastperiode von 16,6 ms (entsprechend 16 600 Taktzyklen) kann man bei geeigneter Programmierung schon eine ganze Menge machen. Die Abtastfrequenz ist aber nicht das einzig wichtige Kriterium bei der Signalverarbeitung. Eine Rolle spielt auch die Genauigkeit, mit der die Abtastwerte dargestellt und verrechnet werden. Natürlich gilt hier: Je genauer, desto besser. Genauigkeit kostet aber wieder Rechenzeit, sobald man die Wortlänge des verfügbaren Prozessors (hier leider nur 8 Bit) überschreitet. Die Arithmetik-Routinen des Basic-Interpreters arbeitet zum Beispiel im Fließkommaformat mit 32-Bit-Mantisse. Sie bietet damit eine Genauigkeit, die selbst für sehr anspruchsvolle Probleme aus der Signalverarbeitung mehr als genug sein dürfte. Diese Routinen sind jedoch so langsam, daß sie auch in 16,6 ms nichts Vernünftiges tun können. Wir werden also unsere eigenen Arithmetik-Befehlsfolgen programmieren müssen und dabei einen Kompromiß zwischen Genauigkeit und Geschwindigkeit machen. Gleitkomma-Arithmetik ist zu aufwendig und für unsere Zwecke auch gar nicht erforderlich. Eine Genauigkeit von nur 8 Bit reicht allerdings auch nicht immer aus. So haben ja auch manche SID-Parameter eine Länge von 12 oder 16 Bit. Im Programm Modulator wird größtenteils mit 16-Bit-Zweierkomplex-Größen gerechnet. Es sei in diesem Zusammenhang auf dem Assembler-Kurs (Teil 3 im 64’er, Ausgabe 11/84) verwiesen, wo ausführlich beschrieben wird, wie man negative Zahlen im Zweierkomplement darstellt. Addition und Subtraktion von Zweierkomplement-Größen werden direkt durch die CPU-Befehle ADC und SBC sowie durch drei Flaggen (Negativ, Carry und Overflow) unterstützt. Für die Multiplikation gibt es dagegen keinen Maschinenbefehl. Da die Multiplikation in Modulator aber eine zentrale Rolle spielt, benötigen wir für sie ein effizientes (das heißt möglichst schnelles) Maschinenprogramm.
Die Multiplikation
Was ist 43 x 13? Die wenigsten Menschen dürften die Antwort auf einen Schlag parat haben, so wie zum Beispiel auf die Frage, was 3 x 7 ist. Wir brauchen 3 x 7 nicht auszurechnen, weil wir es auswendig wissen. Den Wert des Produkts 43 x 13 werden die wenigsten auswendig kennen und daher zu rechnen anfangen. Eine solche Rechnung könnte (ausführlich) so aussehen:
| (1) | 43 x 13 |
| (2) | 43 |
| (3) | 129 |
| (4) | 559 |
In Zeile (1) stehen dabei noch einmal die Faktoren. Zeile (2) stellt das Teilprodukt 43 x 10 = 430 dar, Zeile (3) das Teilprodukt 43 x 3 = 129. Durch geeignetes Einrücken braucht man die Null bei 430 in Zeile (2) nicht mitschreiben. In Zeile (4) werden schließlich die Teilprodukte addiert. Dieser vertrauten Rechenweise liegt das Distributivgesetz zugrunde, welches die Bildungvon Teilprodukten erlaubt:
| (5) | 43x(10+3)=(43x10)+(43x3) |
Die »komplizierte« Multiplikation 43 x 13 wird also auf »einfachere« Multiplikationen 43 x 10 und 43 x 3 zurückgeführt. Bezeichnen wir in unserem Beispiel die Zahl 43 als Multiplikant (MD) und 13 als Multiplikator (MR), so können wir das Multiplikationsschema so formulieren: »Multipliziere MD mit den einzelnen Dezimalstellen von MR und addiere die Teilproduktion, die mit den entsprechenden Zehnerpotenzen 1,10,1000 etc. zu skalieren sind. Die Skalierung erreicht man aber einfach durch Linksverschieben um 0,1,2 etc. Dezimalstellen.«
Man kann den Multiplikator aber auch anders zerlegen, zum Beispiel in Zweierpotenzen:
| 13 = 8 + 4 + 1 |
und so multiplizieren:
| (6) | 43x13 = | 8x43 | + | 4x43 | + | 1x43 |
| = | 344 | + | 172 | + | 43 | |
| = | 599 |
Man benötigt hier als Summanden Produkte von MD mit Zweierpotenzen, die man leicht durch wiederholtes Verdoppeln von MD erhalten kann. Auf diese Weise sollen übrigens schon die alten Ägypter multipliziert haben. Wenn man nun MD und MR im Binärsystem darstellt, kann man besonders einfach multiplizieren: Die Produkte von MD mit Zweierpotenzen erhält man ganz einfach durch wiederholtes Linksverschieben. In unserem Beispiel gilt in binärer Schreibweise: MD = 101011, MR = 1101. Es ergibt sich das Schema:
| MD | MR | |
| (7) | 101011 x 1101 | |
| (8) | 101011 | |
| (9) | 101011 | |
| (10) | + 101011 | |
| (11) | 1000101111 | |
In Zeile (7) stehen MD und MR. Die Zeilen (8), (9) und (10) entsprechen den Teilpodukten 43 x 8, 43 x 4 und 43 x 1, die durch Linksverschiebung aus MD hervorgehen. Die Summe in Zeile (11) ist genau die Binärdarstellung von 559 (nachrechnen!).
Nach diesem Schema kann man nun einen Algorithmus formulieren: Es sei dazu N die Zahl der Binärstellen von MR:
| 1 | SUM:=0; |
| 2 | FOR I:=N-1 DOWNTO 0 DO |
| 3 | BEGIN |
| 4 | SUM := LINKS(SUM); |
| 5 | IF MR(I)=1 THEN SUM:=SUM+MD |
| 6 | END |
Der Algorithmus ist hier formal in einem Pascal-ähnlichen Stil dargestellt. SUM wird zunächst mit 0 vorbesetzt und dann N-mal nach links geschoben. Immer wenn dabei, von links nach rechts gezählt, in MR eine Eins auftritt, wird MD zu SUM addiert.
Sehen wir uns für unser Beispiel einen Trace des Programms an:
| MD = 101011 | MR = 1101 | N = 4 |
| Zeile | I | MR(I)=1 | SUM | AKTION |
| 1 | undef | undef | 0 | |
| 4 | 3 | true | 0 | LINKS |
| 5 | 3 | true | 101011 | + |
| 4 | 1 | true | 1010110 | LINKS |
| 5 | 2 | true | 10000001 | + |
| 4 | 1 | false | 100000010 | LINKS |
| 5 | 1 | false | 100000010 | nichts |
| 4 | 0 | true | 1000000100 | LINKS |
| 5 | 0 | true | 1000101111 | + |
Wir wollen diesen Algorithmus nun konkret in Maschinensprache realisieren. Wenn MD und MR zunächst auf 8 Bit begrenzt werden, kann man auf sie mit einem einzigen Maschinenbefehl zugreifen. Die Variable SUM hält man am besten im Akkumulator, weil man sie zum Addieren sowieso dorthin laden müßte. Auch die Linksverschiebung des Akkumulators ist wesentlich schneller als die einer Speicherzelle. Beim Addieren in den Akkumulator und beim Linksverschieben treten allerdings Überträge auf, die nicht verloren gehen dürfen, da diese je gerade die höherwertigen Bits von SUM darstellen. Das Endprodukt, das sich in SUM bildet, kann bis zu 16 Bit lang werden. (In unserem Beispiel sind es immerhin schon 9 Bit.) Bild 1 zeigt eine elegante Realisierung des Algorithmus, die mit nur zwei Speicherplätzen auskommt.
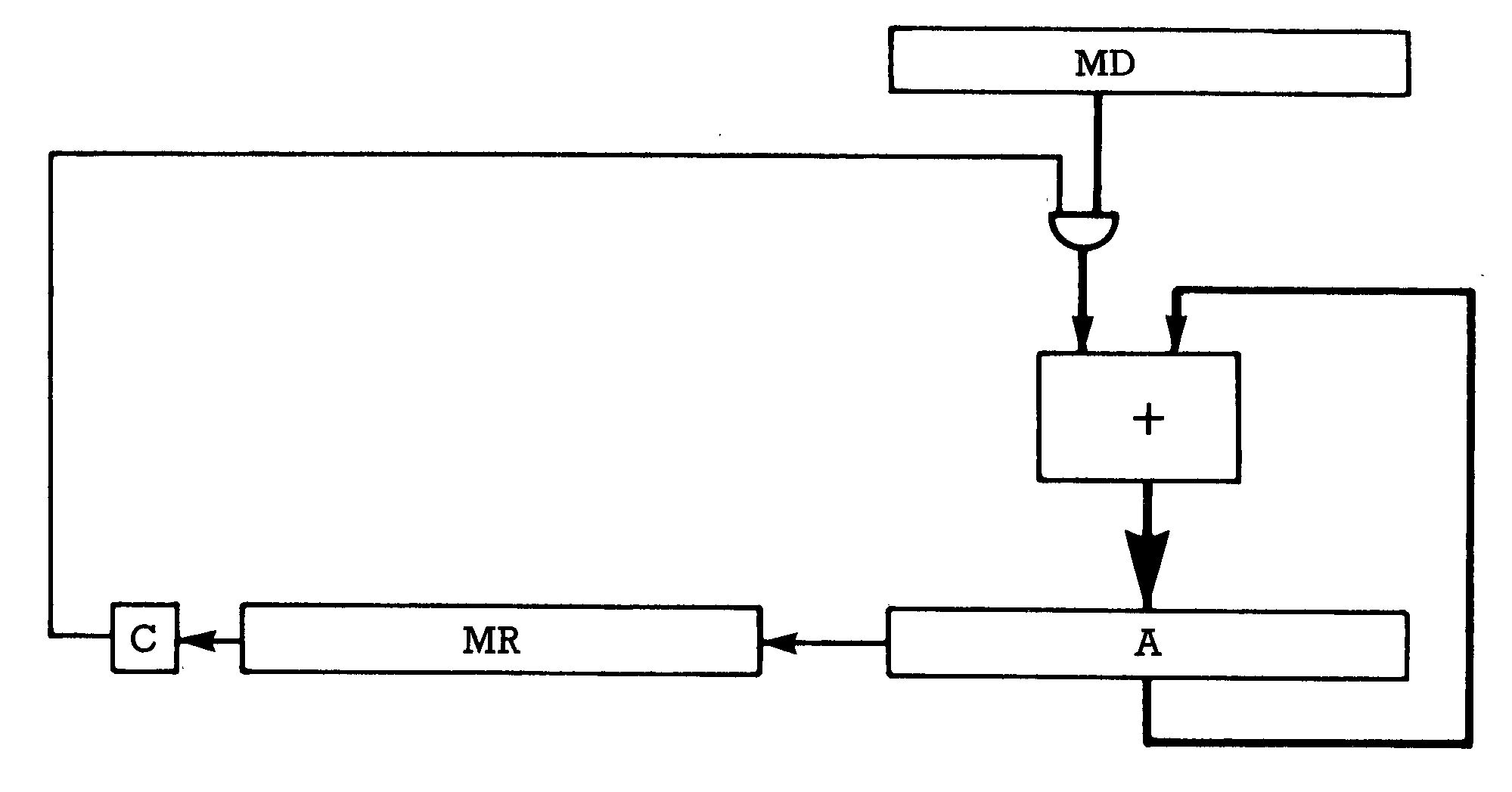
Die langen Rechtecke stellen die Speicherstellen MD, MR und den Akkumulator dar, fette Linien stehen für Bytepfade, dünne für Bitpfade. »+« versinnbildlicht die Addition A : = A + MD. In diesem Schema werden MR und A zusammen (wie ein 16-Bit-Register) nach links geschoben. Dadurch erscheinen die Bits von MR nacheinander in der Carry-Flagge und können so leicht abgefragt werden. MD wird nur dann zum Akku addiert, wenn das durch Linksverschiebungen aus MR gewonnene Bit Eins ist. Ein Übertrag bei der Addition in den Akku muß natürlich nach MR weitergegeben werden, da MR gleichzeitig auch die höherwertigen Bits von SUM enthält. Durch die doppelte Nutzung der Speicherstelle MR wird der Multiplikator zwar durch das höherwertige Byte von SUM überschrieben, man spart sich dadurch aber einen Schiebebefehl und einen Speicherplatz. Da wir wegen schnelleren Zugriffs MD und MR in der Zero-Page plazieren werden, und da der freie Platz dort knapp ist, ist die Einsparung von Speicherplatz durchaus gerechtfertigt. Hier das Programm, das ausführlich besprochen werden soll:
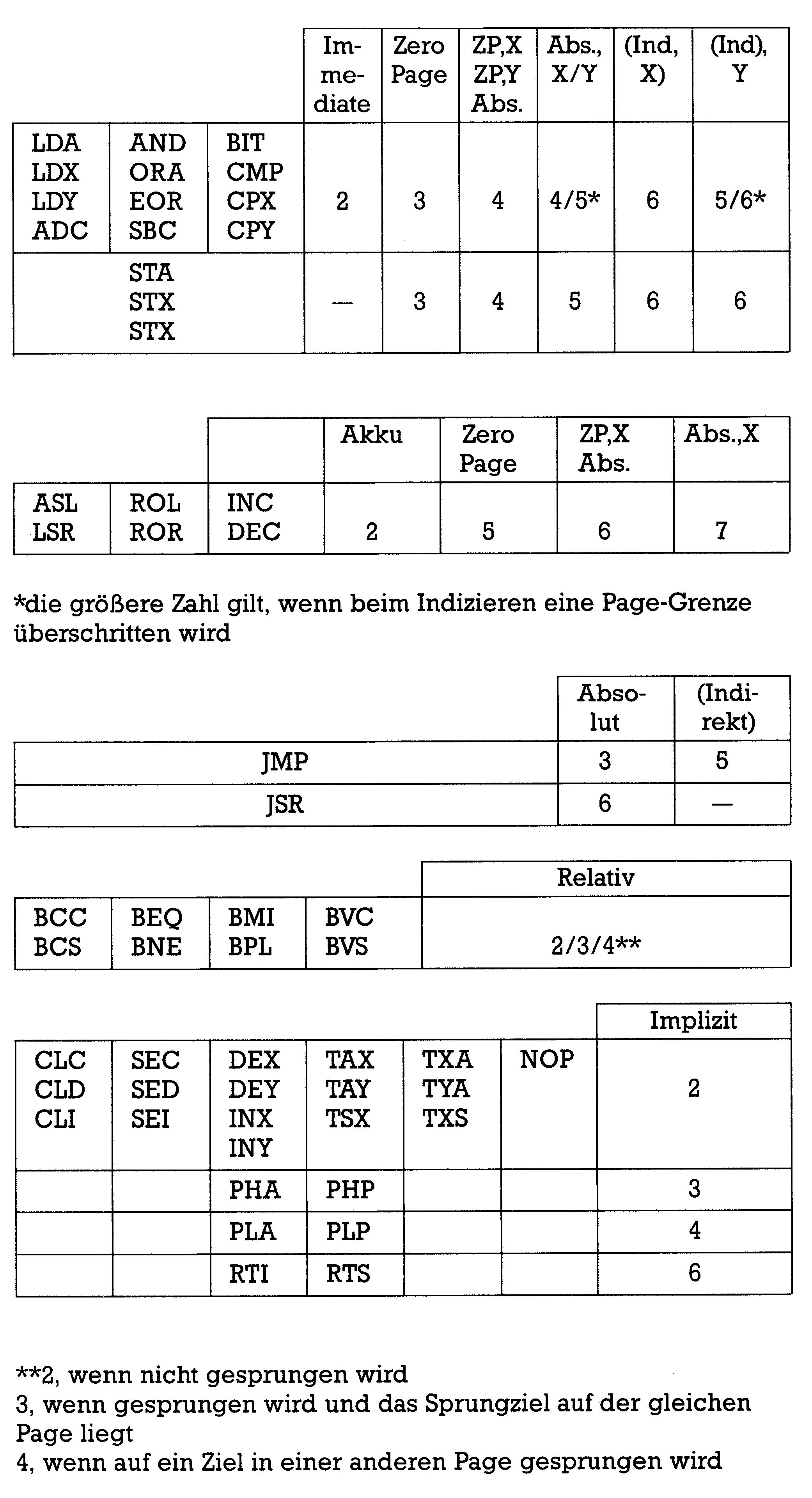
| MUL | LDA #0 | (2) | SUM:=0 |
| LDX #8 | (2) | Schleifenzähler | |
| LOOP | ASL A | (2) | Registerpaar |
| ROL MR | (5) | (MR.A) n. links | |
| BCC NEXT | (2/3) | ||
| CLC | (2) | ||
| ADC MD | (3) | SUM:= SUM+MD | |
| BCC NEXT | (2/3) | ||
| INC MR | (5) | Übertrag nach MR | |
| NEXT | DEX | (2) | |
| BNE LOOP | (2/3) | nächster Lauf |
Die Zahlen in Klammern geben die Ausführungszeiten der Befehle in Taktzyklen an. Sie sind aus Tabelle 1 entnommen. Bei den Verzweigungen nehmen wir der Einfachheit halber an, daß keine Page-Grenzen übersprungen werden, sonst müßte man im Falle eines Sprunges vier statt drei Takte in Rechnung stellen. Zur Arbeitsweise des Programms: Zuerst wird SUM mit 0 vorbesetzt. Dazu genügt es, den Akku mit 0 zu besetzen, da die höherwertigen Bits von SUM erst durch den Schiebeprozeß entstehen. Das X-Register zählt die Schleifendurchläufe. Innerhalb der Schleife wird zunächst das Registerpaar (MR.A) durch das Befehlspaar ASL,ROL nach links verschoben. Beide Befehle schieben nach links, wobei Bit 7 in die Carry-Flagge geschoben wird. Der Unterschied der beiden Befehle besteht aber darin, daß ASL das Bit 0 immer mit Null besetzt, während ROL Bit 0 mit dem Wert besetzt, den die Carry-Flagge vor dem ROL-Befehl hatte. In unserem Fall ist das gerade das aus dem vorhergehenden ASL stammende Bit 7 vom Akku. Nach der Verschiebung zeigt das aus MR stammende Carry-Bit an, ob MD zu SUM addiert werden soll oder nicht. Falls nicht, wird mit BCC NEXT die Addition übersprungen. Die Addition selbst berücksichtigt durch ein weiteres BCC NEXT/INC MR einen eventuell auftretenden Übertrag nach MR. Die Speicherstelle MR enthält zwar gleichzeitig Teile vom Multiplikator und von SUM, man kann sich aber überlegen, daß ein Übertrag nach MR nur den SUM-Teil, aber nicht den Multiplikator-Teil beeinflußt. Nach dem Verlassen der Schleife steht schließlich das 16-Bit-Produkt (die Variable SUM) im Registerpaar (MR.A). Der Multiplikator wurde überschrieben, der Multiplikant in MD dagegen ist unverändert erhalten geblieben.
Zeitbedarf
Es soll hier exemplarisch gezeigt werden, wie man den genauen Zeitbedarf eines Maschinenprogramms ermittelt. Die Ausführungszeit des Multiplikationsprogramms ist nicht einheitlich. Sie hängt von den Anfangswerten von MR und MD ab, welche das Verhalten des Programms an den beiden Verzweigungsstellen (BCC NEXT) beeinflussen. Wir werden hier also den günstigsten (in bezug auf die Rechenzeit) und den ungünstigsten Fall untersuchen. Im ungünstigsten Fall muß bei jedem Schleifendurchlauf addiert werden, und zusätzlich tritt bei jeder Additon ein Übertrag auf. Der Zeitbedarf eines Schleifendurchlaufes beträgt dann:
2(ASL) + 5(ROL) + 2(BCC) + 2(CLC) + 3(ADC) + 2(BCC) + 5(INC) + 2(DEX) + 3(BNE) = 26 Takte
Die Gesamtdauer der Multiplikation ergibt sich dann so:
2(LDA) + 2(LDX) + 8*26(Schleife) -1 = 211
Die -1 kommt dadurch zustande, daß beim letzten Schleifendurchlauf bei BNE nicht gesprungen wird und dadurch nur 2 statt 3 Takte benötigt werden.
Im günstigsten Fall (MR = 0, die Addition wird immer übersprungen) braucht die Schleife:
2(ASL) + 5(ROL) + 3(BCC) + 2(DEX) + 3(BNE) = 16 Takte
Gesamtdauer:
2(LDA) + 2(LDX) + 8*16 (Schleife)-1 = 131
Die Ausführungszeit der Multiplikation liegt also immer zwischen 131 und 211 Takten, wobei die Grenzwerte wohl selten erreicht werden dürften. Man kann im Mittel wohl mit zirka 170 Takten rechnen. Es ist für unsere Zwecke sehr wichtig, diese Größe zu kennen. Wenn wir in unserem Programm Modulator für einen Schritt eine Zeit von maximal 16,6 ms zur Verfügung haben, so können wir daraus eine theoretische Obergrenze für die Anzahl der in einem Schritt ausführbaren Multiplikationen ableiten. Sie liegt bei unserer 8-mal-8-Bit-Multiplikation etwa bei 75, wenn man den ungünstigsten Fall zugrundelegt.
Multiplikation mit größerer Wortlänge
Bei Modulator wird die Multiplikation für folgende Zwecke benötigt: Die LFOs und der Hüllkurvengenerator erzeugen Werteverläufe mit maximaler Amplitude. Das bedeutet bei der 16-Bit-Zweierkomplement-Arithmetik, in der hauptsächlich gerechnet wird, daß die Werte den zur Verfügung stehenden Bereich von -32768 bis +32767 meistens voll ausschöpfen. Nun möchte man aber oft das Modulationsziel, zum Beispiel die Frequenz einer SID-Stimme, nur um einige Hertz nach oben und unten modulieren. Man möchte die Tiefe dieser Modulation aber auch möglichst kontinuierlich steuern können, so daß zum Beispiel auch Modulationstiefen von einer Quinte oder gar einer Oktave möglich sind. Aus diesem Grund muß das Modulationssignal erst mit einem geeigneten Skalierungsfaktor multipliziert werden. Anschließend kann es durch einfache Addition zur Zielgröße diese in dem gewünschten Sinn modulieren.
Bei der Modulation von Tonhöhen ergibt sich außerdem noch ein weiteres Problem: Dort kommt es nicht auf absolute, sondern auf relative Frequenzverschiebungen an. Ein Beispiel: Ein 500-Hz-Ton wird um ±5 Hz moduliert. Um bei einem 1000-Hz-Ton den gleichen Effekt zu erzielen, muß man ihn um ± 10 Hz modulieren. Der Modulationsbetrag muß also bei Tonhöhen zusätzlich mit der zu modulierenden Frequenz selbst skaliert werden, was eine weitere Multiplikation erforderlich macht.
Die Wortlängen der Modulationsziele sind:
| Tonfrequenzen | 16 Bit |
| Pulsweiten | 12 Bit |
| Filterfrequenz | 8 Bit |
| Lautstärke | 4 Bit |
Die Filterfrequenz ist beim SID zwar eine ll-Bit-Größe, da aber feine Frequenzunterschiede in der Filterfrequenz nicht hörbar sind, werden nur die oberen 8 Bit moduliert.
Zur Steuerung der Modulationstiefe genügen 8-Bit. Eine fein gestufte Modulation ist ohnehin nur bei der Tonhöhenmodulation erforderlich. Hier genügt es aber, wenn das Modulationssignal selbst einen fein gestuften Verlauf (16 Bit) hat. Die durch 8 Bit realisierbaren 255 verschiedenen Modulationstiefen reichen aus, um alles vom feinsten Vibrato über Tonhöhensprünge in allen musikalisch sinnvollen Intervallen bis hin zur Sirene mit weitem Frequenzbereich zu verwirklichen.
Wir benötigen also eine 16 x 8-Bit-Multiplikation. Der Algorithmus von Bild 1 ließe sich in diese Richtung leicht erweitern. Man kann etnweder MR auf 16 Bit verlängern und benötigt dann 16 statt 8 Schleifendurchläufe oder man verlängert MD und A auf 16 Bit. In letzterem Fall benötigt man weiterhin nur 8 Schleifendurchläufe wobei aber, im Falle einer Eins aus MR, zwei 16-Bit-Größen (MD und A) addiert werden müssen. Natürlich braucht man für das höherwertige Byte von A einen weiteren Speicherplatz in der Zero-Page.
In Modulator wird ein anderer Weg eingeschlagen. Er wird durch Bild 2 beschrieben. Dieses erscheint zwar zunächst sehr kompliziert, daszugehörige Programm benötigt aber eine geringere Ausführungszeit. Vorgegeben sind ein 16-Bit-Multiplikator im Registerpaar (MR + 1.MR) und ein 8-Bit-Multiplikant in MD (Der Einfachheit halber werden hier Zero-Page-Speicherplätze »Register« genannt.) Das Ergebnis des Programms soll ein 24-Bit-Produkt im Register Tripel (MR + 1.MR.A) sein.
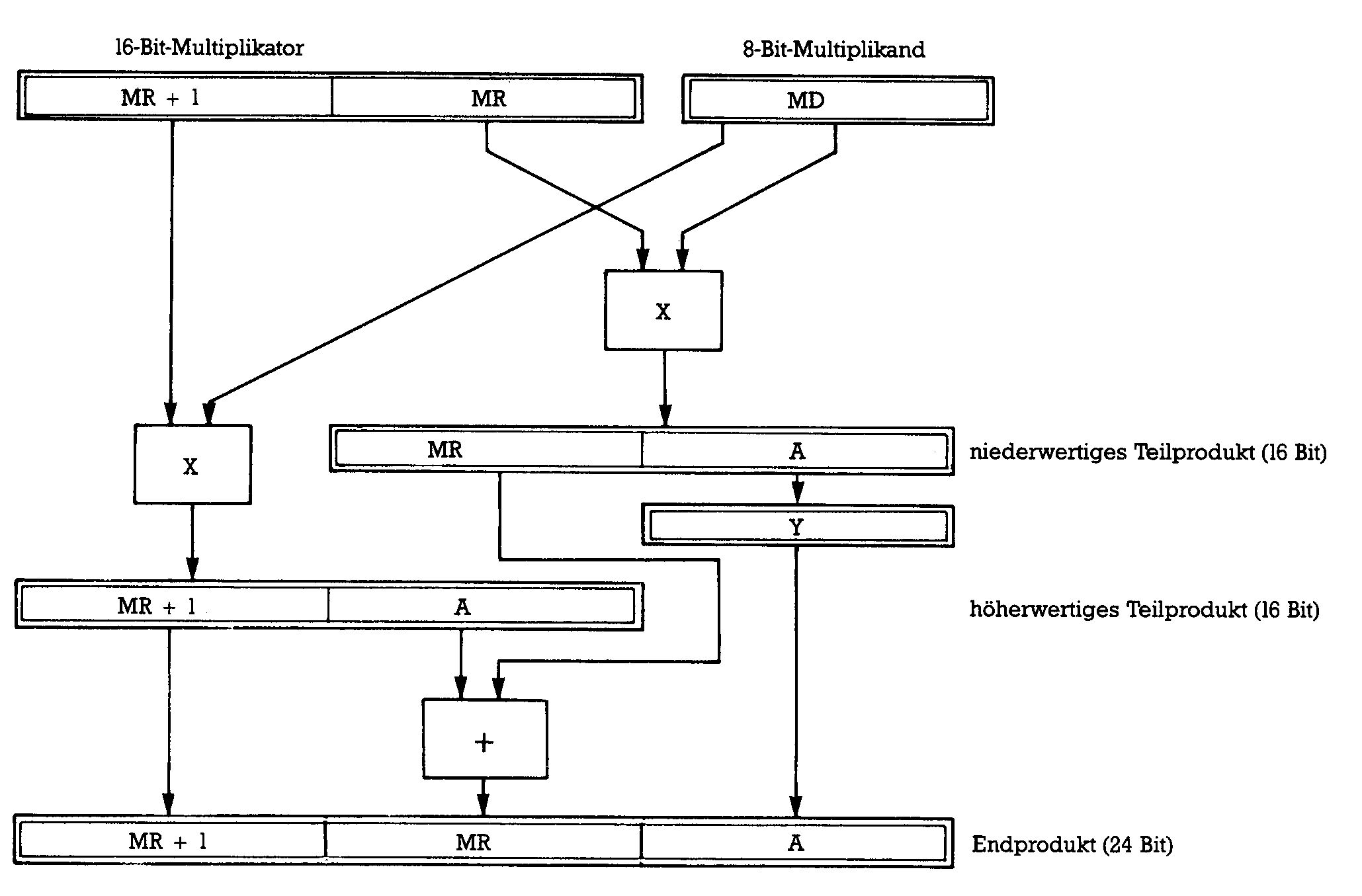
Zuerst wird das niederwertige Teilprodukt MR x MD gebildet. Das Rechteck mit dem Kreuz steht für das Verfahren aus Bild 1, welche wie schon beschrieben, ein 8 x 8-Bit-Produkt in (MR.A) liefert. A wird im Y-Register zwischengspeichert. Anschließend werden MR +1 und MD ebenfalls nach Bild 1 multipliziert. Das Ergebnis ist das höherwertige Teilprodukt in (MR + l.A). Schließlich müssen die Teilprodukte nur noch mit richtiger Skalierung addiert werden. Dazu wird das höherwertige Byte des niederwertigen Teilprodukts, das in MR steht, zum niederwertigen Byte des höherwertigen Teilprodukts, das sich schon im Akku befindet, addiert. Dabei muß ein eventueller Übertrag nach MR +1 berücksichtigt werden. Das niederwertige Byte des niederwertigen Teilprodukts wird nur noch vom Y-Register in den Akku übertragen, wo es den niederwertigsten Teil des Endprodukts darstellt. In Modulator werden allerdings grundsätzlich nur 16-Bit-Größen weiterverarbeitet, so daß diese untersten 8 Bit des Produktes unberücksichtigt bleiben.
Im Source Listing zu Modulator steht das zugehörige Programm MULU in den Zeilen 1680 bis 1970. Zunächst steht dort zweimal hintereinander das schon vorgestellte 8 x 8 Bit-Multiplikationsprogramm, anschließend werden ab Zeile 1910 die Teilprodukte addiert. Eine Analyse ergibt eine Laufzeit von minimal 282 Takten und maximal 446 Takten.
Alle bisher beschriebenen Multiplizierer arbeiten nur dann korrekt, wenn man die Faktoren als positive Ganzzahlen interpretiert. Sie sind ohne Ergänzung nicht für Zweierkomplement-Größen geeignet. Das Programm MULS ab Zeile 2020 ist eine solche Ergänzung. Es berücksichtigt das Vorzeichen des Multiplikators. Ist dieser positiv, so wird sofort nach MULU verzweigt. Ein negativer Multiplikator wird zunächst negiert, wodurch er positiv wird (Zeile 2040 bis 2100), MULU wird als Unterprogramm aufgerufen, und schließlich wird das positive Produkt noch einmal negiert, was dann ein korrektes Resultat liefert. Der 8-Bit-Multiplikant wird aber nach wie vor nur als positive Zahl behandelt.
Die LFOs
Sie erzeugen die für Modulationen sinnvollen Kurvenverläufe als Folge von 16-Bit-Zweierkomplement-Zahlen. Am häufigsten wird die Dreieckskurve benötigt, da sie keine Sprünge macht und daher bei Anwendung auf Tonhöhen und auf Pulsweiten am angenehmsten klingt. Der Sägezahn eignet sich mehr für »härtere Effekte und für Videospiele, wo stark und schnell modulierte Töne oft zu hören sind. Die Rechteckkurve eignet sich für Triller (bei Frequenzmodulation), für mandolinenartige Effekte (bei Modulation von Lautstärke und Filterfrequenz) sowie für rhythmische Effekte (bei Frequenzmodulation mit größerer Modulationstiefe).
Rechnerisch kann man einen Sägezahnförmigen Wertverlauf besonders einfach erzeugen. Bei Modulator wird einfach ein 16-Bit-Wert zyklisch hochgezählt. Zyklisch bedeutet, daß immer wieder beim Minimalwert angefangen wird, wenn der Maximalwert überschritten wird. Das geschieht bei begrenzter Wortlänge automatisch durch Überlauf, den man hier absichtlich unberücksichtigt läßt. Im Modulator-Programm wird der Werteverlauf durch das Wort (= Bytepaar) SAWUP repräsentiert. SAWUP wird einfach um den Betrag im Wort LFOF hochgezählt. Dadurch ist die resultierende Frequenz der Sägezahnkurve direkt proportional zum Wert LFOF. Im Programm wird in Zeile 2300 bis 2420 erst das Steuerregister LFOC abgefragt. Im Falle des HOLD- oder RESET-Status braucht nichts berechnet zu werden. Im Falle des RUN-Status wird SAWUP in den Zeilen 2430 bis 2510 hochgezählt. Der aufsteigende Sägezahn wird dann gewissermaßen als »Master« für die anderen Kurvenformen herangezogen. Bild 3 zeigt, wie diese aus SAWUP gewonnen werden.
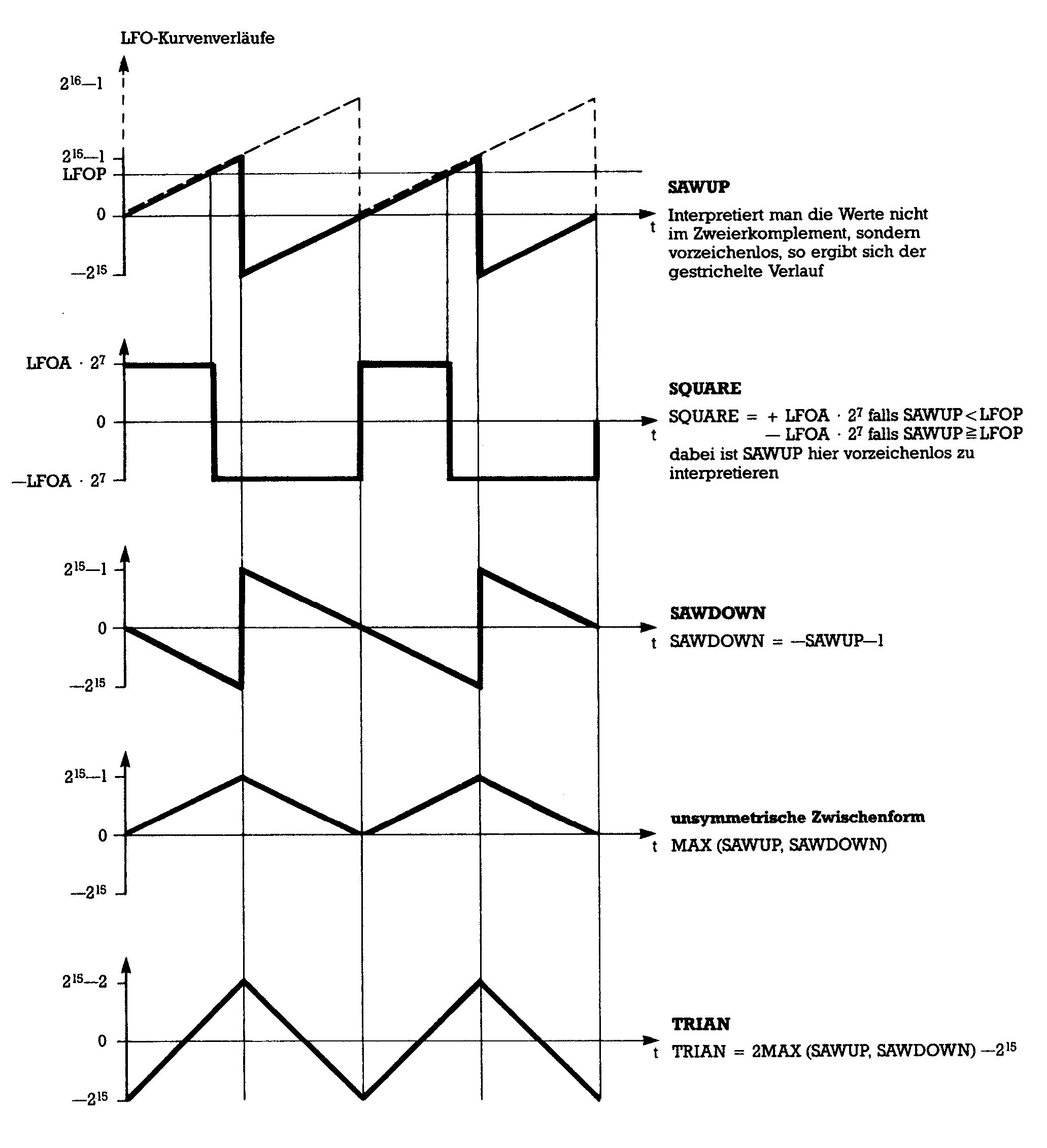
Interessant ist, daß gleichgültig, ob man die SAWUP-Werte im Zweierkomplement oder grundsätzlich positiv interpretiert, sich immer der gleiche Kurvenverlauf ergibt (gestrichelte und durchgezogene Kurve bei SAWUP).
Die Rechteckkurve entsteht dadurch, daß man, gesteuert durch SAWU, zwischen den Extremwerten + LFOA x 2 (hoch) 7 und -LFOA x 2 (hoch) 7 hin- und herschaltet. Man spart sich so die sonst anschließend fällige Multiplikation mit der LFO-Amplitude (= Modulationstiefe) LFOA. Hin- und hergeschaltet wird, wenn der Sägezahnwert einen vorgegebenen Schwellwert über- beziehungsweise unterschreitet. Dieser Schwellwert ist nichts anderes als die Pulsweite LFOP. SAWDOWN erhält man einfach durch Negieren von SAWUP. Bildet man das Maximum von SAWUP und SAWDOWN, so erhält man einen dreieckförmigen Kurvenverlauf, der allerdings nur positive Werte annimmt. Durch Verdoppeln dieser Werte und Verschiebung um 2 (hoch) 15 nach unten erhält man dann eine symmetrische Dreieckskurve maximaler Amplitude.
Im Programm wird in Zeile 2530 bis 2590 aus LFOC ermittelt, welche Kurvenform überhaupt erzeugt werden soll, und entsprechend weiterverzweigt. Mit Ausnahme des Rechtecks, das schon mit seiner endgültigen Amplitude aufwartet, wird der errechnete Wert noch mit der Amplitude LFOA multipliziert (Zeile 3090 bis 3170). Das LFO-Programm rechnet alle 7 LFOs. Dabei wird auf die jeweiligen Parameter indiziert zugegriffen. Das Byte LFONR enthält dazu einen Adreß-Offset, der vom LFO-Programm in das X-Register geladen wird. Dieser Offset muß vom Programm, welches das LFO-Programm aufruft, korrekt zur Verfügung gestellt werden.
Aliasing-Parasitäre Frequenzen
Bei der eben beschriebenen Erzeugung der LFO-Kurvenformen tritt bei etwas höheren Frequenzen, etwa ab 10 Hz, noch ein interessantes Phänomen auf. Man kann die Erzeugung eines Sägezahnverlaufs durch zyklisches Hochzählen eines Wortes auch als Abtastung einer hypothetischen, kontinuierlichen Sägezahnkurfe auffassen. Die Abtastfrequenz ist in unserem Fall mit 60 Hz fest. Die Frequenz der hypothetischen Sägezahnkurve kann man aber durch den Parameter LFOF sehr feinstufig zwischen 0 und 60 Hz variieren. Wie soll aber zum Beispiel eine LFO-Kurve mit 50 Hz aussehen, wenn man nur 60 Abtastwerte pro Sekunde hat? Die Antwort gibt Bild 4. Man erhält den gestrichelten Verlauf mit einer Frequenz von nur 10 Hz. Noch seltsamer sieht das Resultat bei einer LFO-Frequenz von 25 Hz aus. Die Folge der Abtastwerte schwingt zwar ungefähr im Rhythmus von 25 Hz, dieser Bewegung ist aber zusätzlich ein Auf und Ab im 10-Hz-Rhythmus überlagert.
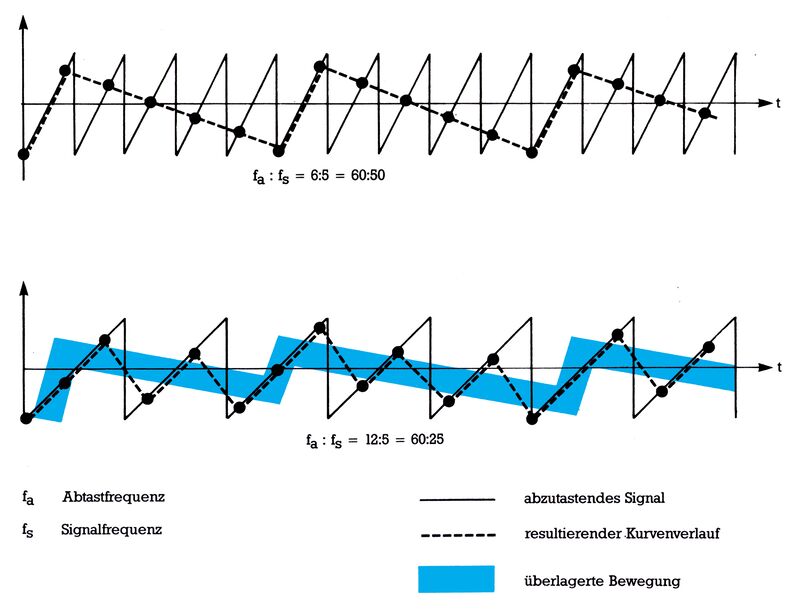
Der theoretische Hintergrund dieser Erscheinung sei hier nur gestreift: Nach dem Abtasttheorem muß die Abtastfrequenz mindestens doppelt so hoch sein, wie die höchste im abzutastenden Signal vorkommende Frequenz, damit die Abtastfolge dieses Signal richtig repräsentiert. Andernfalls weist die Abtastfolge Frequenzanteile auf, die im Originalsignal gar nicht vorkommen. Man nennt diesen Effekt Aliasing (von lat. alias = anderswo). In unserem Fall können die Bedingungen des Abtasttheorems nie vollständig erfüllt werden, da der ideale Sägezahn Obertöne beliebig hoher Ordnung enthält. Im ersten Fall von Bild 4 wird das Abtasttheorem grob verletzt: Die Abtastfrequenz ist bei weitem nicht doppelt so groß wie die Signalfrequenz. Als Resultat tritt nur eine Aliasing-Frequenz von 10 Hz auf. Im zweiten Fall wird das Abtasttheorem immerhin für die Grundschwingung des Signals erfüllt. 60 Hz ist mehr als doppelt so groß wie 25 Hz. Die 25 Hz sind in der Folge der Abtastwerte auch erkennbar. Die zweite Harmonische des Signals ist aber mit 50 Hz schon zu hoch für die Abtastung. Ihre Amplitude beträgt immerhin die Hälfte der Amplitude der Grundschwingung, wie eine Fourier-Analyse ergibt. Und genau diese Harmonische findet man auch hier als eine Aliasing-Frequenz von 10 Hz in der Folge der Abtastwerte wieder.
Aliasing tritt auch schon bei niedrigeren LFO-Frequenzen als 25 Hz auf. Der Effekt wird dann aber schwächer, weil die dafür verantwortlichen Obertöne von höherer Ordnung und damit von niedrigerer Amplitude sind. Mit dem Aliasing-Effekt kann man bei bewußtem Einsatz zusätzliche interessante Modulationen verwirklichen.
Wie es weitergeht
Nach diesem etwas anstrengenden theoretischen Teil werden wir uns in der nächsten Folge wieder der Tonerzeugung selbst zuwenden. Zunächst werden noch der Hüllkurvengenerator und der Portamento-Mechanismus von Modulator beschrieben, anschließend wird ein komfortables Editorprogramm vorgestellt, das ein schnelles, interaktives Manipuleren aller Modulator- und SID-Parameter ermöglicht. Mit dem Programm kann direkt über die Tastatur gespielt werden, und es können Sound-Parametersätze auf Diskette verwaltet werden. Dieses Programm soll dann in einer weiteren Folge zu einem kompletten dreistimmigen Sequenzer erweitert werden. Als Besonderheit wird dieses Programm unabhängige Melodier/Sound-Files erzeugen können, die für sich allein lauffähig sind. Die so erstellten Klangschöpfungen können dann in andere Programme eingebaut werden.
(Thomas Krätzig/aa)
