Reise durch die Wunderwelt der Grafik (Teil 6)

Nachdem wir in der letzten Folge die Sprites, einen Leckerbissen unseres Computers, kennengelernt haben, wenden wir uns — nach zwei anderen Grafikeigenheiten des C 64 — wieder der hochauflösenden Grafik zu, die wir einige Zeit sträflich vernachlässigt haben. Diese nützen wir dann für zwei- und dreidimensionale Darstellungen auf dem Bildschirm aus.

Zunächst aber ein leichtes und ein schwierigeres Thema:

Wenn Sie an Ihrem Computer eine Kassettenstation verwenden, dann kennen Sie das ja zur Genüge. Sie geben irgendeinen Kassettenbefehl ein, der Computer fordert zum Beispiel PRESS RECORD & PLAY. Sobald Sie dieser Aufforderung nachgekommen sind, ist der Bildschirm total leer. Dieses üble Verhalten — wir sehen ja nun einige Meldungen nicht mehr — hat seinen Grund. Die Kassettenoperationen können etwas schneller laufen. Überhaupt beschleunigt ein abgeschalteter Bildschirm einen Programmablauf. Im allgemeinen nützt uns das nicht viel, denn wir reden ja mit unserem Computer per Bildschirm und wenn der Gesprächspartner einen »black-out« hat, kann nicht miteinander verkehrt werden. Manchmal gibt es aber Situationen, wo dieses Abschalten für kurze Zeit ganz angenehm sein kann. Wenn wir zum Beispiel ein kompliziertes Titelbild aufbauen, mögen viele nicht zuschauen. Sondern nach einem leeren Bildschirm soll sofort das fertige Titelbild auftauchen.

Was passiert beim Abschalten des Bildschirmes? Das ist optisch eigentlich gar nicht so aufregend, denn der ganze Bildschirm nimmt die Farbe des Rahmens ein. Er wird also genau genommen nicht abgeschaltet. Geschaltet wird etwas, das wir nicht sehen können. Nämlich eine ganz bestimmte Fähigkeit unseres Prozessors, auf den Systembus anders als im Normalbetrieb zuzugreifen. Diese Art des Zugriffs birgt eine versteckte, mögliche Fehlerquelle: Wenn während Kassettenoperationen Sprites angeschaltet bleiben, können Störungen beim Zugriff auf Daten auftreten. Falls Sie die erste Folge dieser Artikelserie noch vorliegen haben, dann können Sie in Tabelle 1 nachsehen (Registerübersicht). In Register 17 (Adresse 53265) dient das Bit 4 als Schaltbild für Bildschirm »aus« oder »an«. Wenn wir dieses Bit auf 0 setzen, erblindet der Monitor. (Da hatte sich in die Tabelle 1 ein Fehler eingeschlichen: Dort steht’s genau umgekehrt). Wie Sie noch aus den anderen Folgen wissen, ist dieses Register 17 ein ziemlich komplexes Ding. Wir müssen also darauf achten, daß nur Bit 4 gesetzt oder gelöscht wird. Ich hoffe, daß Sie noch wissen, wie das ging. Zur Erinnerung:
Normaler Inhalt von 53265:
XXX1 XXXX
AND 239:
1110 1111
Jetzt ist Bit 4 gelöscht:
XXX0 XXXX
Das entspricht dem Befehl:
POKE 53265,PEEK(53265)AND239
Nun noch zum Wiedereinschalten des Bildschirmes:
Mit gelöschten Bit 4:
XXX0 XXXX
OR 16:
0001 0000

Normaler Inhalt wieder hergestellt:
XXXI XXXX
In Basic ist das dann:
POKE53265,PEEK(53265)OR16.

Zum Ausprobieren ein kleiner Dreizeiler:
10 POKE 198,0:WAIT 198,1:POKE 53265,PEEK(53265)AND 239
15 PRINTCHR$(147):POKE 211,15:POKE 214,10:SYS 58640:PRINT "HALLO”
20 POKE 198,0:WAIT 198,1:POKE 53265,PEEK(53265)OR16

Nach RUN wartet das Programm auf einen Tastendruck, auf den hin dann der Bildschirm »ausgeschaltet« wird. Ein weiterer Tastendruck macht das Bild dann wieder sichtbar.

Nebenbei bemerkt: Falls Sie einige POKEs und das SYS-Kommando nicht kennen, hier die Erklärung: 198 ist das Byte, in dem die Anzahl gedrückter Tasten gespeichert wird. Deswegen kann man mit WAIT 198,1 und vorher erfolgtem Nullsetzen dieses Bytes dasselbe erreichen, wie mit der häufig benutzten GET-Abfrage. SYS 58640 ist ein Einsprung in die Betriebssystemroutine, die den Cursor setzt. Die gewünschte Spalte wird in Byte 211, die Zeile in 214 eingePOKEt. Damit erspart man sich den Wust an Cursorsteuerzeichen, die dem Drucker Kopfschmerzen bereiten können.

Das sogenannte Scrollen: Bildverschiebung

Wir kennen jetzt fast alle Register des VIC-II-Chips. Zwei Bytes, nämlich 53265 und 53270, bergen noch Geheimnisse, die wir nun lüften wollen. Zunächst die Bits 3. Sie enthalten normalerweise den Wert 1. Jetzt ändern wir das mal in 53265:
POKE 53265,PEEK(53265)AND247 (RETURN)

Haben Sie’s bemerkt? Wenn nicht, dann zählen Sie mal die Zeilen auf dem Bildschirm nach: Es sind nur noch 24 zu sehen. Rückgängig können Sie das wieder machen durch Setzen des Bit 3:
POKE 53265,PEEK(53265)OR8 (RETURN)

Probieren wir dasselbe mit der Speicherstelle 53270:
POKE 53270,PEEK(53270)AND247 (RETURN)
Unsere Kommandos sehen jetzt etwas merkwürdig aus und auch der Cursor. Wir haben nicht mehr 40 Spalten, sondern nur noch 38 zur Verfügung. Zurück in den Normalzustand:
POKE 53270,PEEK(53270)OR8 (RETURN)

Beim Eingeben dieser Zeile werden Sie bemerkt haben, daß trotzdem noch der ganze 40-Zeichen-Bereich zur Verfügung steht, nur sind die erste und letzte Spalte verdeckt. Der Rahmen ist breiter geworden und versteckt gewissermaßen den Rand des Bildschirmes.

Nun kommen wir zum Scrollen. Das englische Wort »scroll« heißt auf Deutsch etwa Rolle oder Schriftrolle. Wenn wir ein längeres Programm listen oder mit dem Cursor an den unteren Bildrand fahren, rollt der C 64 den Bildschirminhalt nach oben. Das ist ein zeilenweises Scrollen. Der VIC-II-Chip gestattet aber auch eine andere Art des Scrollens, die im englischen als »smooth scrolling«, etwa »fließendes« Scrollen bezeichnet wird. Wie Sie sich sicherlich erinnern, ist jedes Zeichen aus 8 Bytes zusammengesetzt. Während beim erstgenannten Scrollen alle 8 Bytes (also ein Zeichen) auf einmal nach oben springen, geht das beim fließenden Scrollen Byte für Byte. Dazu dienen die Bits 0 bis 2 der Register 53265 und 53270. Sehen wir uns das mal in Einzelschritten an. Der Maximalwert in den 3 Bits (0,1,2) kann 7 sein (binär 111). Alle anderen Bits müssen geschützt sein. Normalerweise steht in 53265 in den Bits 0 bis 2 der Wert 3 und an derselben Stelle in 53270 der Wert 0. Folgendes Kurzprogramm soll diese Werte mit jedem Tastendruck verändern:
5 PRINT CHR$(147)CHR$(166)
10 FOR I = 0 TO 7
20 POKE 53265,(PEEK(53265)AND 248)OR I
30 GETA$:IFA$ = ""THEN30
40 NEXTI
50 POKE 53265,(PEEK(53265)AND 248)OR3

Wenn Sie dieses Programm starten, wandelt das Grafikzeichen bei jedem Tastendruck Byte für Byte herunter. Wenn Sie jetzt noch einfügen:
7 POKE 53265,PEEK(53265)AND 247
das war ja das Einführen des 24-Zeilen-Modus, dann ist das Grafikzeichen zu Anfang fast versteckt. Wir sollten dann aber auch noch den Normalzustand wiederherstellen am Programmende:
60 POKE 53265,PEEK(53265)OR8

Auf diese Weise geschieht das fließende Scrollen nach unten. Verändern wir Zeile 10:
10 FOR I = 7 TO 0 STEP —1
dann erfolgt Scrollen nach oben.

Das gleiche Programm können wir mit kleinen Änderungen für horizontales Scrollen verwenden. Wir müssen nur überall dort, wo 53265 steht, jetzt 53270 und in Zeile 50 anstelle von OR3 jetzt OR0 einsetzen. Wenn Sie Zeile 10 mit der Rückwärtsschleife belassen haben, scrollt der Bildschirminhalt nach links. Ändern Sie dagegen Zeile 10 wieder zur ursprünglichen Vorwärtsschleife, dann erfolgt ein Scrollen nach rechts. Sie werden jetzt sagen, daß das alles ja ganz nett ist, aber was kann man damit tun? Damit kann man Laufschriften erzeugen, die in beliebiger Richtung über den Bildschirm sausen oder schleichen — je nachdem. Leider, leider kommen wir hier langsam aber sicher an die Grenzen von Basic. Denn jetzt taucht ein Problem auf, dessen Lösung — in Basic als auch in Maschinensprache — gleich ein zweites nach sich zieht. Sehen wir uns zunächst Problem Nummer 1 an:

In dem Moment, wo man das Zeichen geduldig Byte für Byte aus dem Versteck herausgeholt hat, also 7 in die Bits 0 bis 2 von 53265 oder 53270 eingegeben hat, muß man ja dafür sorgen, daß

1. der Bildschirminhalt um ein Zeichen weitergeschoben wird,
2. im Versteck (am Rand) ein nächstes Zeichen parat liegt.

Dazu können wir uns zum Beispiel des ohnehin schon eingebauten Zeilen-Scrolls bedienen, wie im nachfolgenden Programm:
10 POKE 53265,PEEK(53265)AND 247
20 PRINTCHR$(147):FOR I = 1 TO 24:PRINTCHR$(17);:NEXT I
30 POKE 53265,(PEEK(53265)AND 248)OR7
40 PRINT"SCROLLING NACH OBEN”
50 FORI = 6TO0STEP-1
60 POKE53265,(PEEK(53265)AND-248)OR I:FORJ=1TO 50:NEXT J
70 NEXTI:GOTO30

Wenn Sie dieses Programm gestartet haben, können Sie mit RUN/STOP und RESTORE den Normalzustand wiederherstellen. Haben Sie etwas bemerkt? Ein Flackern des Bildes trat auf. Das ist das zweite Problem, auf das wir gleich kommen werden.

Ein Beispiel für das horizontale Scrollen gibt das Programm von H. Gehrmann in Happy-Computer, Ausgabe 4/84, Seite 108f. H. Gehrmann hat es geschafft, in Basic tatsächlich fließendes Scrollen ohne Bildschirmflackern zu erzeugen. In Zeile 36 seines Programms ist ein Teil seiner Lösung für Problem Nummer 2 zu finden. Dort steht:
36 IF PEEK(53265) < > 155 THEN 36

Erst danach druckt er an den oberen Bildschirmrand die zu scrollende Textzeile und scrollt dann, wie wir es bisher kennengelernt haben. Was ist denn nun dieses zweite Problem? Sehen wir dazu zunächst einmal in die Speicherstelle 53265 hinein. Geben Sie (nach NEW) mal die folgende Textzeile ein:
10 PRINT PEEK(53265):GOTO10

Nach RUN sehen Sie eine Reihe aus 27 und ab und zu taucht 155 auf. Wenn Sie jetzt mit RUN/STOP und RESTORE dieses Testprogramm angehalten haben, sehen wir uns diese Zahlen mal binär an:
27 = binär 0001 1011
155 = binär 1001 1011

Alle Bits kennen wir schon, außer Bit 7, welches sich verändert hat. Es handelt sich um das msb des Rasterzeilen-Registers. Das LSB davon findet sich in Speicherzelle 53266. Wir haben es hier mit einer 9stelligen Binärzahl zu tun, von der 8 Stellen (die Bits 0 bis 7) in 53266 und die 9. Stelle als Bit 7 in 53265 zu finden sind. Gezählt werden ständig in diesen neun Bits die Rasterzeilen. Sie werden sich fragen, was das soll, hier ist die Antwort:

An der Entstehung eines Fernsehbildes ist ein Elektronenstrahl beteiligt. Er tastet Punktzeile für Punktzeile von oben nach unten den Bildschirm ab und erzeugt dabei das Bild. 20 mal in der Sekunde baut er ein neues Bild auf, und in welcher Punktzeile (Rasterzeile) er gerade ist, das zählt der Computer mit in diesem Rasterzeilenregister. Er muß deshalb mitzählen, weil er dem Elektronenstrahl einige Informationen übergeben muß, nämlich ob ein Punkt sichtbar sein soll oder nicht. Der Zeilenstrahl überstreicht den gesamten Bildschirm, also auch Bereiche, die außerhalb des lesbaren Textfensters liegen. Deswegen müssen wir auch weiter als bis 255 Rasterzeilen zählen. Weil aber in ein Byte (hier nun 53266) nur bis 255 gezählt werden kann, kommt noch das Bit 7 von 53265 als msb dazu.

Jedesmal, wenn der Zeilenstrahl über die 255. Rasterzeile hinaushuscht, wird dieses Bit gleich 1. Das Problem Nummer zwei läßt sich also jetzt so ausdrücken: Wenn eine Bildänderung stattfindet, während der Zeilenstrahl über die Änderungsstelle hinwegstreicht, kommt es zu Zuckungen des Bildes. Man muß dafür sorgen, daß man diesem Flitzer nicht ins Gehege kommt. H. Gehrmann hat das in seinem Programm so gemanagt, daß er den Bildinhalt verändert, während der Rasterstrahl außerhalb des sichtbaren Bereiches arbeitet. Trotzdem gibt es hier aber noch Schwierigkeiten. Ein ganzer Bildschirm besteht aus 280 Rasterzeilen. Wenn man nun nachrechnet, braucht der Elektronenstrahl zirka 180 Microsekunden zum Überstreichen einer Rasterzeile, das heißt, er ist in sehr kurzer Zeit wieder im sichtbaren Bereich! Bis dahin muß die Bildveränderung abgeschlossen sein. Normalerweise ist das eine Aufgabe für Maschinenprogramme, von denen Sie einige in der nachfolgend genannten Literatur finden:

• R. Babel, M. Krause, A. Dripke: Das Interface Age Systemhandbuch zum Commodore 64, München 1983, S. 63-64,
• A. Plenge: Das Grafikbuch zum Commodore 64, Düsseldorf 1984, S. 272ff.

Dornröschen ist wieder dran: 2D-Grafik besser

Von nun an kümmern wir uns wieder um Dornröschen, die hochauflösende Grafik. Wie Sie wohl spätestens in Folge 4 bemerkt haben, ist das Koordinatensystem, das unser Commodore 64 auf dem Bildschirm einrichtet, reichlich unüblich. Zur Erinnerung sehen Sie sich mal Bild 1 an.

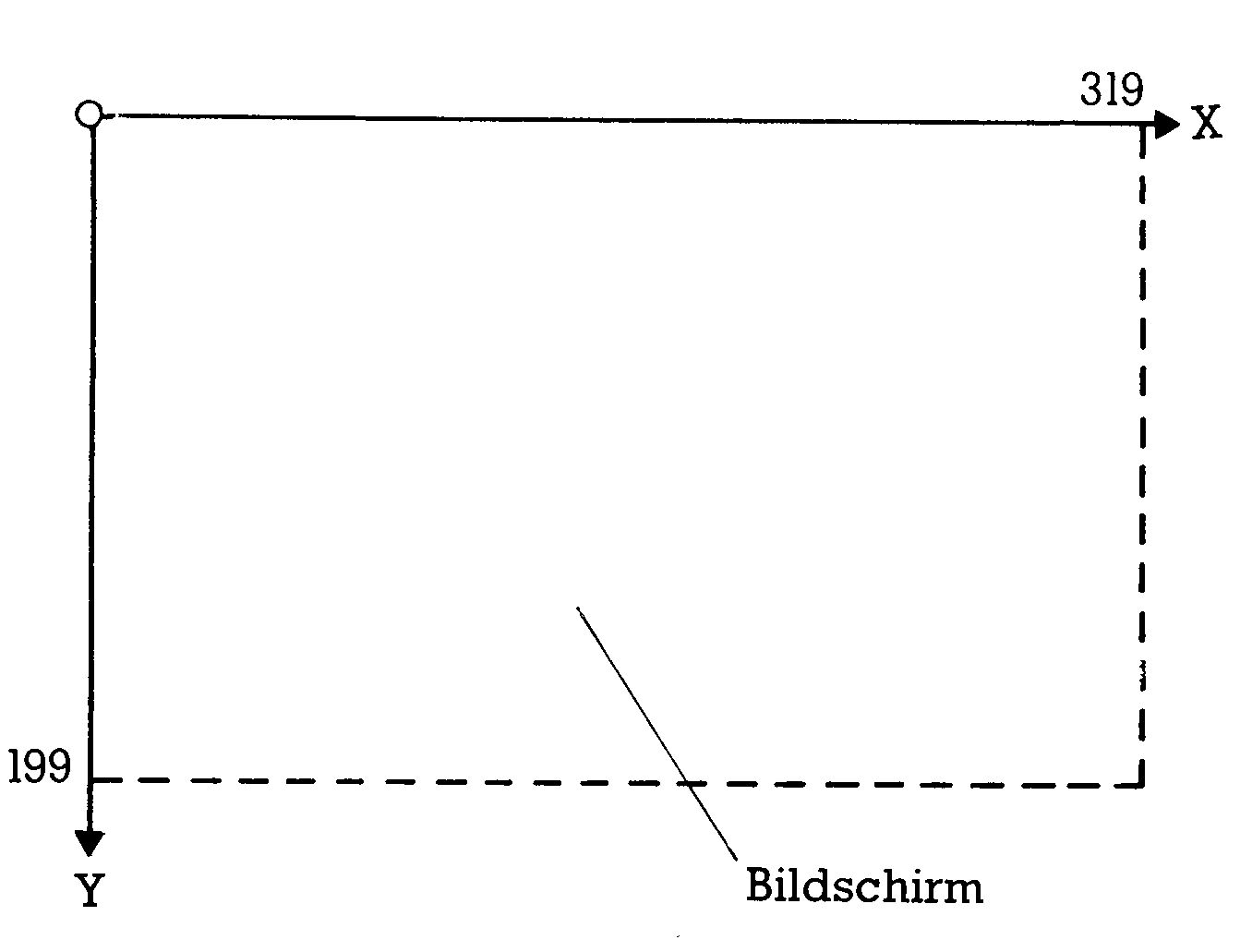
Wie Sie aus der Schule vielleicht noch wissen, ist die normale Darstellung eines Koordinatensystems aber so wie in Bild 2 gezeigt.

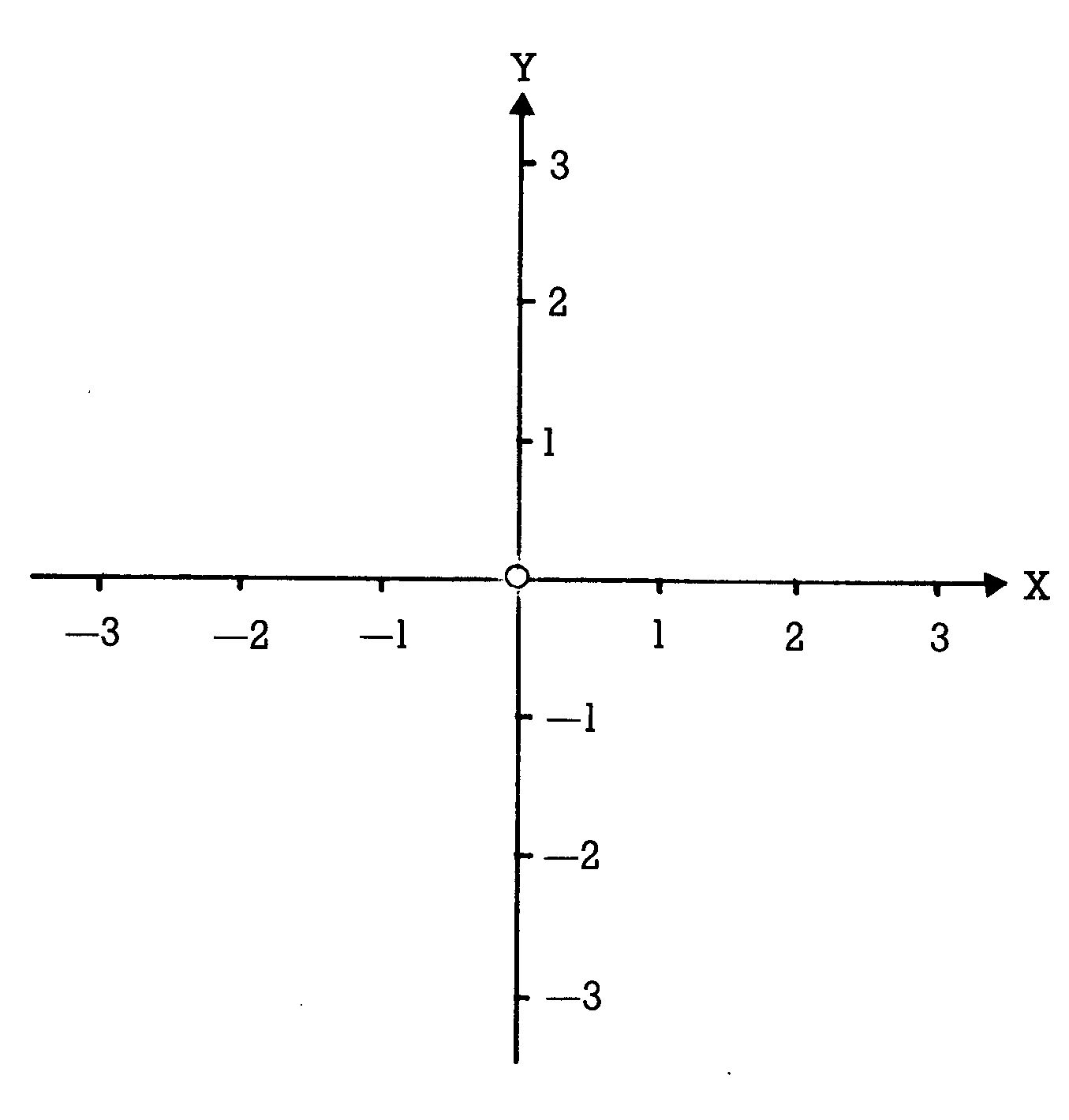
Im Listing 3 der 4. Folge mußte deshalb eine einfache Sinus-Funktion so verändert werden, daß man sie von der Formel her kaum mehr erkennen kann (Zeile 5). Bleiben wir beim Beispiel der Sinus-Kurve. Die sieht so aus wie in Bild 3 gezeigt.

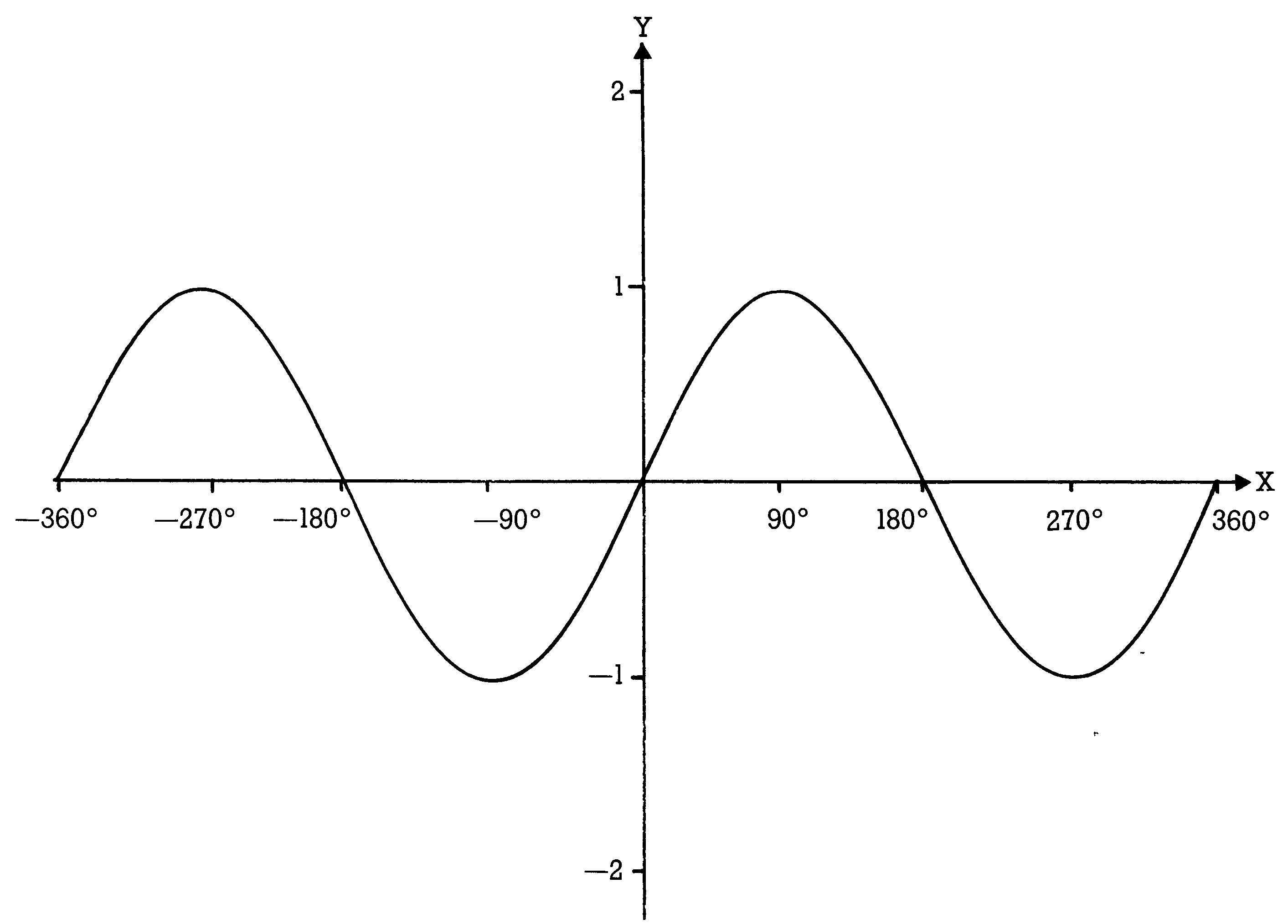
Wie groß oder klein X also auch immer wird, Y bewegt sich nur zwischen +1 und -1 hin und her. Wenn wir aber die normale Sinus-Gleichung (Y=SIN(X)) auf unserem Bildschirmsystem zeichnen lassen, werden wir gar nichts oder kaum etwas sehen (Bild 4).

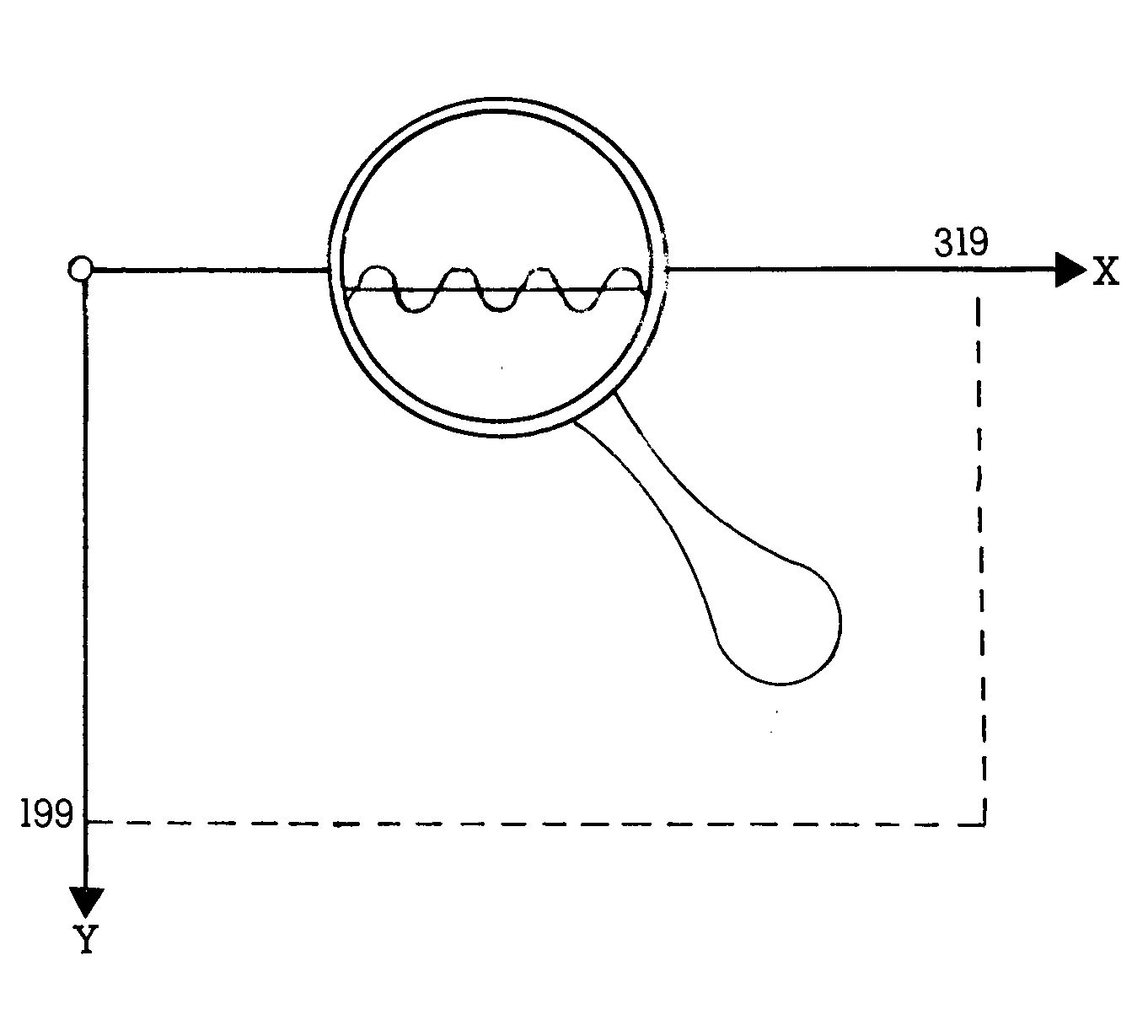
Wir müssen also einen Weg finden, ein uns genehmes Koordinatensystem anstelle des Bildschirmsystems zu verwenden. Dazu soll uns die Mathematik helfen. Man nennt das, was wir jetzt tun werden, eine Transformation! Keine Angst, es wird nicht zu schwierig!

In Bild 5 sind zwei Koordinatensysteme abgebildet.

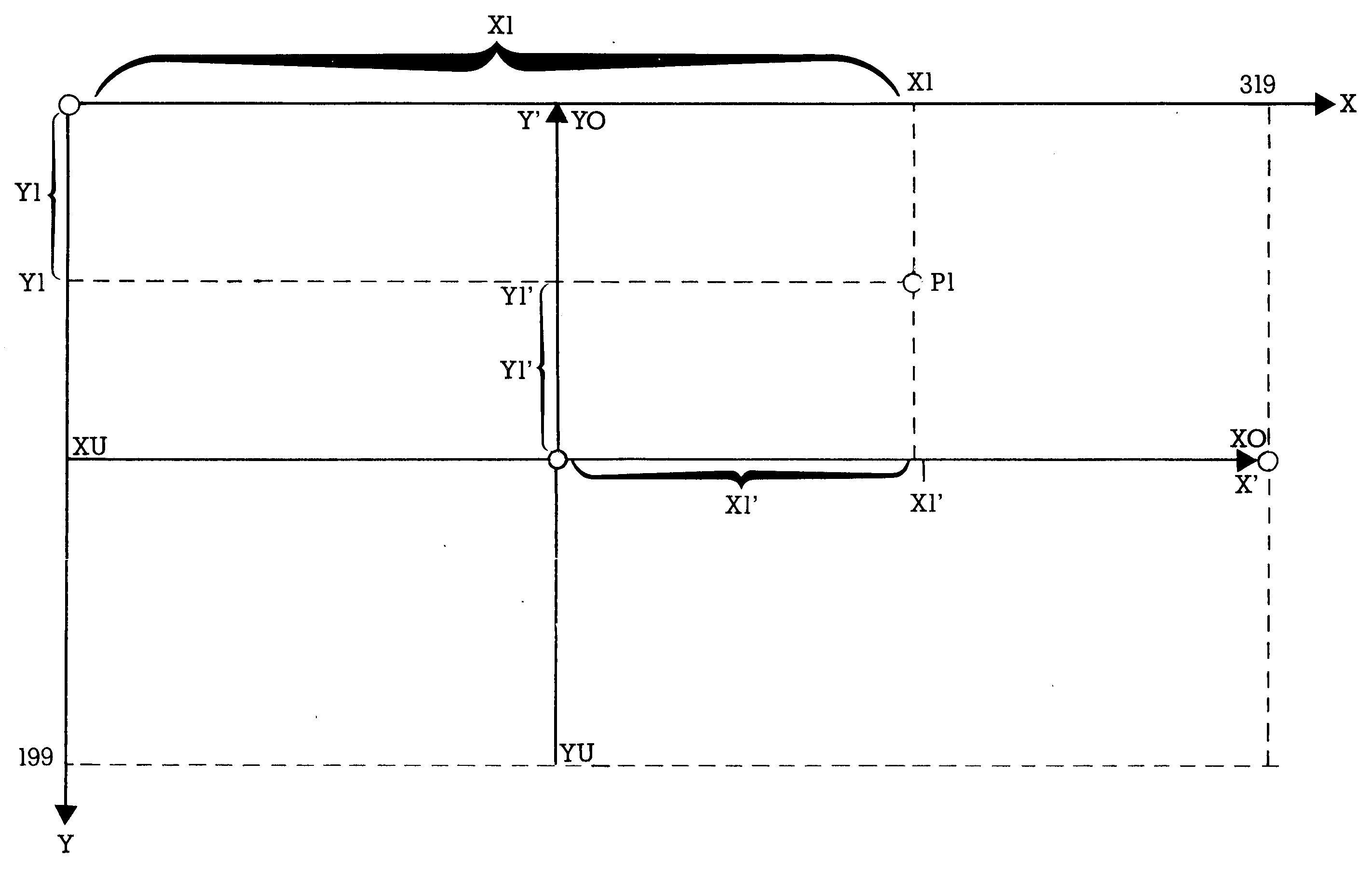
1. Das Bildschirmsystem X, Y mit Nullpunkt 0
2. Das von uns gewünschte System X', Y', mit Nullpunkt O', welches rot gezeichnet ist.

Außerdem ist der Punkt P1 zu sehen. Je nach dem, auf welches Koordinatensystem er bezogen wird, hat er die Koordinaten

1. XI, Y1 oder
2. XI', Y1'.

Unser eigenes System soll vom unteren Wert XU bis zum oberen X-Wert XO reichen und vom unteren Y-Wert YU bis zum oberen YO. Am Beispiel unserer Sinus-Kurve wäre es sinnvoll, die X-Werte von XU=-1 bis XO = 10 und die Y-Werte von YU=-2 bis YO= +2 abzubilden. Die Entfernung von XU bis XO (also XO-XU) erstreckt sich auf 319 Bildpunkte. Man kann nun ein Verhältnis bilden, denn XI muß sich zu (X1-XU)(das ist die Länge der Strecke von XU bis X1') genauso verhalten wie 319 zur Gesamtentfernung(XO-XU). Als Formel sieht das so aus:

X1 / (X1' - XU) = 319 / (XO - XU)

Das einzige in dieser Formel, was wir nicht kennen (X1' ist ja unsere Eingabe, die auf unser eigenes Koordinatensystem bezogen ist) ist nun X1, also die X-Koordinate unseres Punktes P1 im Bildschirmsystem. Man kann diese Verhältnisgleichung nach X1 auflösen:
X1 = (X1' - XU)/(XO - XU)*319

So ähnlich geht das auch bei der Y-Koordinate. Es ist nur zu beachten, daß im Bildschirmsystem die Y-Achse nach unten, in unserem System aber nach oben zeigt. Deswegen ist die Entfernung von YO nach Y1': YO-Y1'. Das Verhältnis hat hier also die Formel:

Y1 / (YO - Y1') = 199 / (YO - YU)

Nach Y1 aufgelöst ergibt sich:
Y1 = (YO-Y1')/(YO-YU)*199

Es empfiehlt sich, diese beiden sogenannten Transformationsgleichungen als Basicfunktionen zu definieren:
DEFFNX(X)=(X-XU)/(XO-XU)*319
DEFFNY(Y)=(YO-Y)/(YO-YU)*199

Nun können wir ein kleines Aufrufprogramm schreiben, welches sich wieder der Unterprogrammsammlung aus Folge vier bedient. Laden Sie also zuerst (die hoffentlich damals gespeicherten!) Unterprogramme und tippen Sie dann ein:
5 POKE 52,92:POKE 56,92
100 DEFFNX(X)=(X-XU)/(XO-XU)*319
110 DEFFNY(Y) = (YO-Y)/)YO-YU)*199
120 REM +++++ BEISPIELFUNKTION +++++
140 DEFFNA(X) = SIN(X)
150 PRINTCHR$(147)CHR$(17): INPUT"XU,XO,YU,YO = ";XU,XO,YU,Y0
160 INPUT"ZEICHEN- UND HINTERGRUNDFARBE = ‘’;F1,F2
170 GOSUB 50100:FOR I = XU TO XO STEP(XO-XU)/319
180 X = FNX(I):Y=FNY(FNA(I)):GOSUB 50040
190 NEXT I:X1 = FNX(XU):Y1 = FNY(O):X2 = FNX(XO):Y2=Y1
GOSBUB 50060
195 X1 = FNX(O):Y1 = FNY(YU):X2 = X1:Y2 = FNY(YO):GOSUB 50060
200 GET A$:IF A$=""THEN 200
210 GOSUB 50030
220 END

Nach RUN und mit der erforderlichen Geduld (kennen Sie ja schon) zeichnet der Computer eine ganz normale Sinuskurve in das von Ihnen durch XU,XO,YU und YO angegebene Koordinatensystem. In die Zeile 140 können Sie jetzt jede beliebige Funktion eingeben. Allerdings ist es unglücklich, daß man jedesmal das Programm ändern muß, nämlich Zeile 140, wenn man eine neue Funktion sehen will. Es gibt da einen Trick, der mit dem Tastaturpuffer arbeitet (Speicherstellen 631-640) und den ich Ihnen nun zeigen möchte. Zunächst fügen wir noch eine Zeile 130 ein:
130 F$ = "SIN(X)"

Wenn das Programm startet, soll man zunächst einmal erfahren, welche Funktion überhaupt in Zeile 140 steht. Deswegen also:
10 PRINTCHR$(147):POKE211,5:POKE214,10:SYS58640:
PRINT"FUNKTION IM PROGRAMM:”
20 PRINT:PRINTTAB(3)"Y= ”F$

Wenn wir das so laufen lassen, wird keine Funktion erscheinen, weil diese dem Computer erst in Zeile 130 mitgeteilt wird. Der Computer muß also vorher nachsehen, als was F$ definiert ist. Deswegen führen wir ein:
15 K=1:GOSUB 130:K = 0
und
145 IFK=1 THEN RETURN

Jetzt druckt das Programm uns die Funktion aus. Als nächstes soll der Computer erfahren, ob die Funktion zu verändern ist:
30 PRINT:PRINTTAB(5)CHR$(18)”A” CHR$(146)"LTE ODER”
CHR$(18)"N"CHR$(146)"EUE FUNKTION?”
35 GET A$:IFA$<>"A" AND A$<>"N" THEN 35

Wenn die alte Funktion gewählt wurde, dann kann alles wie bisher ablaufen:
40 IF A$="A" THEN 100

Ansonsten wollen wir jetzt unseren Trick anwenden. Zunächst das Eingeben der neuen Funktion:
45 PRINT:PRINTTAB (3);:INPUT "Y=";F$
Dann:
50 PRINTCHR$(147)CHR$(17)CHR$ (17)” 130F$ = "CHR$(34)F$CHR$(34)
55 PRINT”140DEFFNA(X) = ”F$
60 PRINT"RUN 100":PRINTCHR$ (19);
65 POKE 631,13:POKE 632,13:POKE 633,13:POKE 198,3:END

Tippen Sie’s ein und fügen Sie in Zeile 100 noch ein STOP ein, damit Sie sehen können, was mit diesen Zeilen passiert. Sie sehen, daß der Bildschirm zunächst frei gemacht wird (CHR$(147) in Zeile 50) und dann zwei Programmzeilen 130 und 140 gedruckt werden mit der neuen Funktion, danach noch die RUN-Anweisung. Der Cursor springt dann wieder in die Ecke links oben (CHR$(19) in Zeile 60). Jetzt arbeitet unser Computer den Inhalt des Tastaturpuffers ab, der aus drei RETURNs (die 13) besteht. Die Anzahl 3 muß in Speicherstelle 198 festgehalten sein. Die Tatsache, daß der Tastaturpuffer abgearbeitet wird, haben wir dem END zu verdanken. Weil aber ein RETURN nach RUN 100 folgt, startet das Programm sofort wieder selbständig ab Zeile 100. Wenn Sie jetzt mal Zeile 130 und 140 listen lassen, steht dort die neue Funktion. Weil sie sich im Programmablauf störend auswirken, sollen die zu druckenden Zeilen unsichtbar werden. Deswegen fügen wir in Zeile 45 noch an:
:POKE 646,6
und ab Zeile 100 soll wieder sichtbar werden, was zu drucken ist, weshalb wir dort anfügen:
:PRINTCHR$(147):POKE 646,14

Dieser Trick ist sehr vielseitig anwendbar. Man muß nur beachten, daß durch das RUN alle Variablen, die bis dahin definiert wurden, gelöscht werden. Das ist ja auch sinnvoll, weil wir das Basicprogramm verändert haben und so unter Umständen Variable überschrieben wurden. Sollte es nicht möglich sein, alle Variablen nach dem Neustart zu definieren, dann läßt sich ein ähnlicher Kniff anwenden, wie wir ihn in Zeile 15 verwendet haben. Probieren Sie das Programm mal mit folgenden Eingaben:

Y= SIN(X) mit XU = -1,XO = 10,YU = -2,YO = 2
oder Y=EXP(-X/10)*COS(X) mit XU = -18,XO = 10,YU=-5,YO = 5 oder Y=2*SIN(X) + SIN(2*X + 2) mit XU = -6,XO = 15,YU = -3,YO = 3
Ihrer Phantasie sind keine Grenzen gesetzt.

Flacher Raum: 3D-Grafik, wie funktioniert das?

Nun sind wir bei dreidimensionalen, also räumlichen Abbildungen angekommen. Zunächst einmal: Es ist klar, weil der Fernsehschirm eben nur eine Fläche ist wie ein Blatt Zeichenpapier, daß wir etwas Räumliches auf einer Fläche darstellen müssen. Alles andere ist Science fiction, auch für die größten Computer! Bei 3D-Darstellungen unterscheidet man hauptsächlich zwei Arten:

1. Zeichnungen, die mit einer Spezialbrille räumlich wahrgenommen werden können,
2. Zeichnungen, die perspektivisch gestaltet sind und deswegen als räumlich empfunden werden.

Im Prinzip ist der Weg a) für uns begehbar. Wir könnten die dazu nötigen zwei verschiedenfarbigen Zeichnungen (meist rot und blau) mit Hilfe des Mehrfarben-Bitmap-Modus erzeugen. Allerdings ist der rechnerische Aufwand nicht unerheblich. Ab und zu werden in Programmzeitschriften entsprechende Entwürfe veröffentlicht.

Der übliche Weg allerdings geht über eine perspektivische Darstellung. Zwei Arten wiederum finden vor allem Anwendung:

1. Die sogenannte Kavaliers-Perspektive
2. Die Perspektive mit mindestens einem Fluchtpunkt.

Den Unterschied soll Bild 6 erläutern.

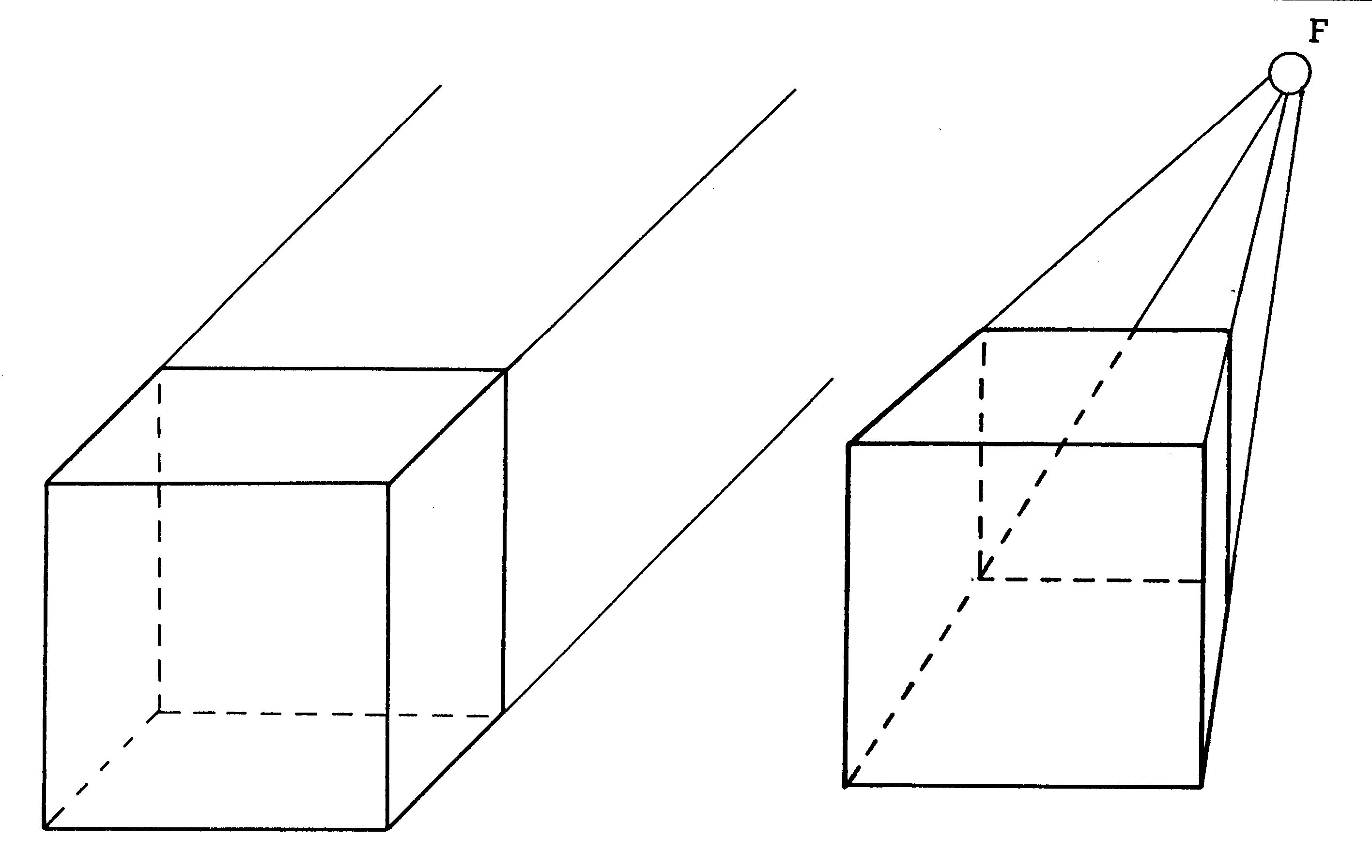
Bei der Kavaliers-Perspektive bleiben alle Linien, die auch in Wirklichkeit parallel verlaufen, parallel, wohingegen sie im anderen Fall in einem Fluchtpunkt zusammenlaufen, wenn sie in die räumliche Tiefe weisen. Gemeinsam ist beiden Verfahren, daß die Linien, die in den Raum verlaufen (also nach hinten oder vorne) verkürzt werden, weil unsere Augen sonst über die Größenverhältnisse täuschen. Zwar sieht die Fluchtpunktperspektive sehr viel natürlicher aus, aber die Kavaliers-Perspektive ist mathematisch bei weitem nicht so kompliziert. Deswegen wollen wir uns mit ihr befassen. Weiterhin schränken wir uns noch ein: Der Winkel, unter dem die Linien in den Raum laufen, soll 45 ° betragen, also ein halber rechter Winkel sein. In diesem Fall verkürzen sich die nach vorne oder hinten verlaufenden Kanten auf die Hälfte. Genauso, wie man einen Punkt durch seine Koordinaten im ebenen System festlegen kann, ist er auch in einem räumlichen Koordinatensystem definierbar. Man baut einfach noch eine dritte Achse (eine in den Raum weisende Z-Achse) zu den vorhandenen dazu und erhält so Zusammenhänge wie in Bild 7.

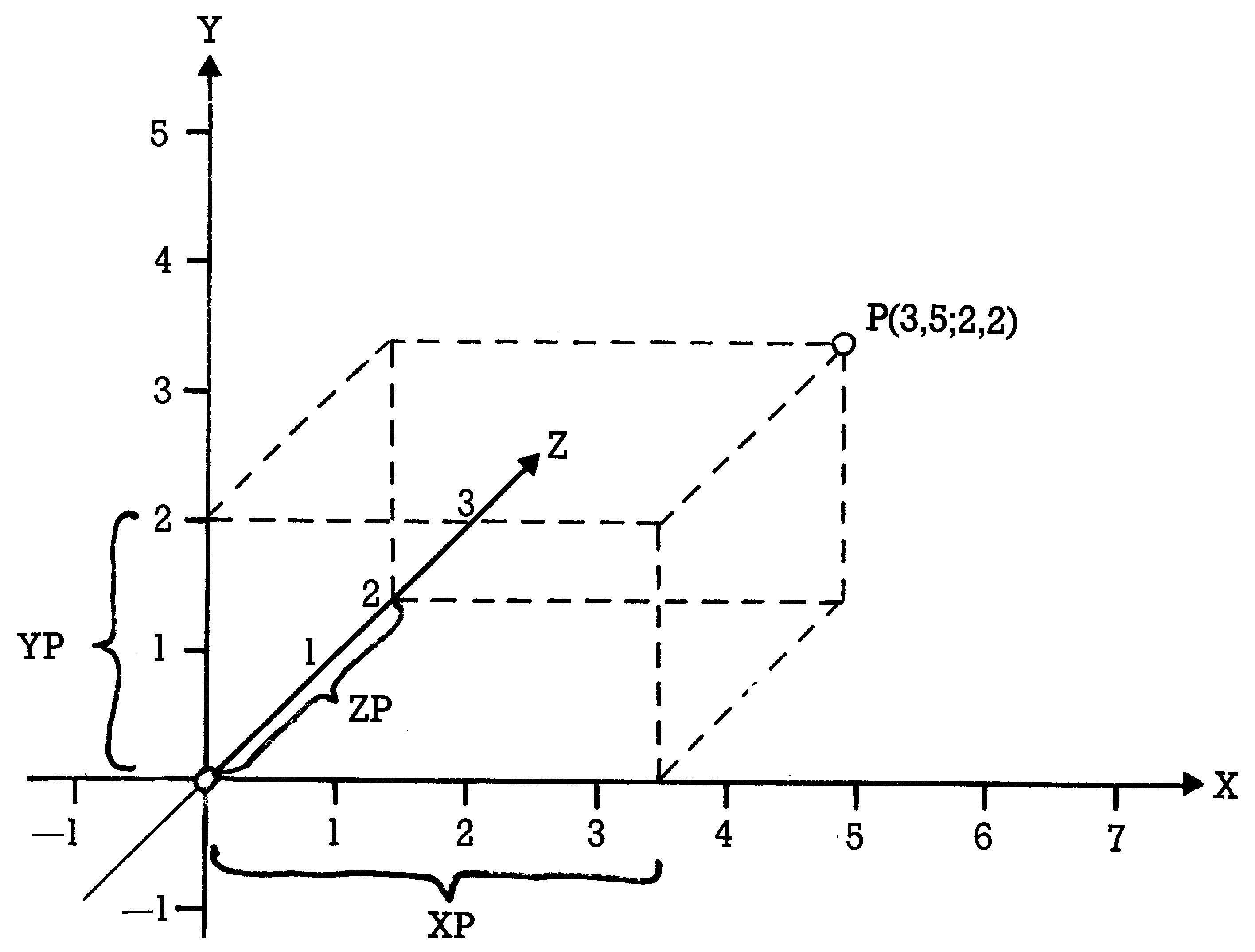
Das Verfahren soll durch diese Erklärung noch etwas verdeutlicht werden. Man kann sich den Raum als eine große Anzahl dicht an dicht hintereinander gestapelter X-Y-Ebenen vorstellen, etwa wie in Bild 8.

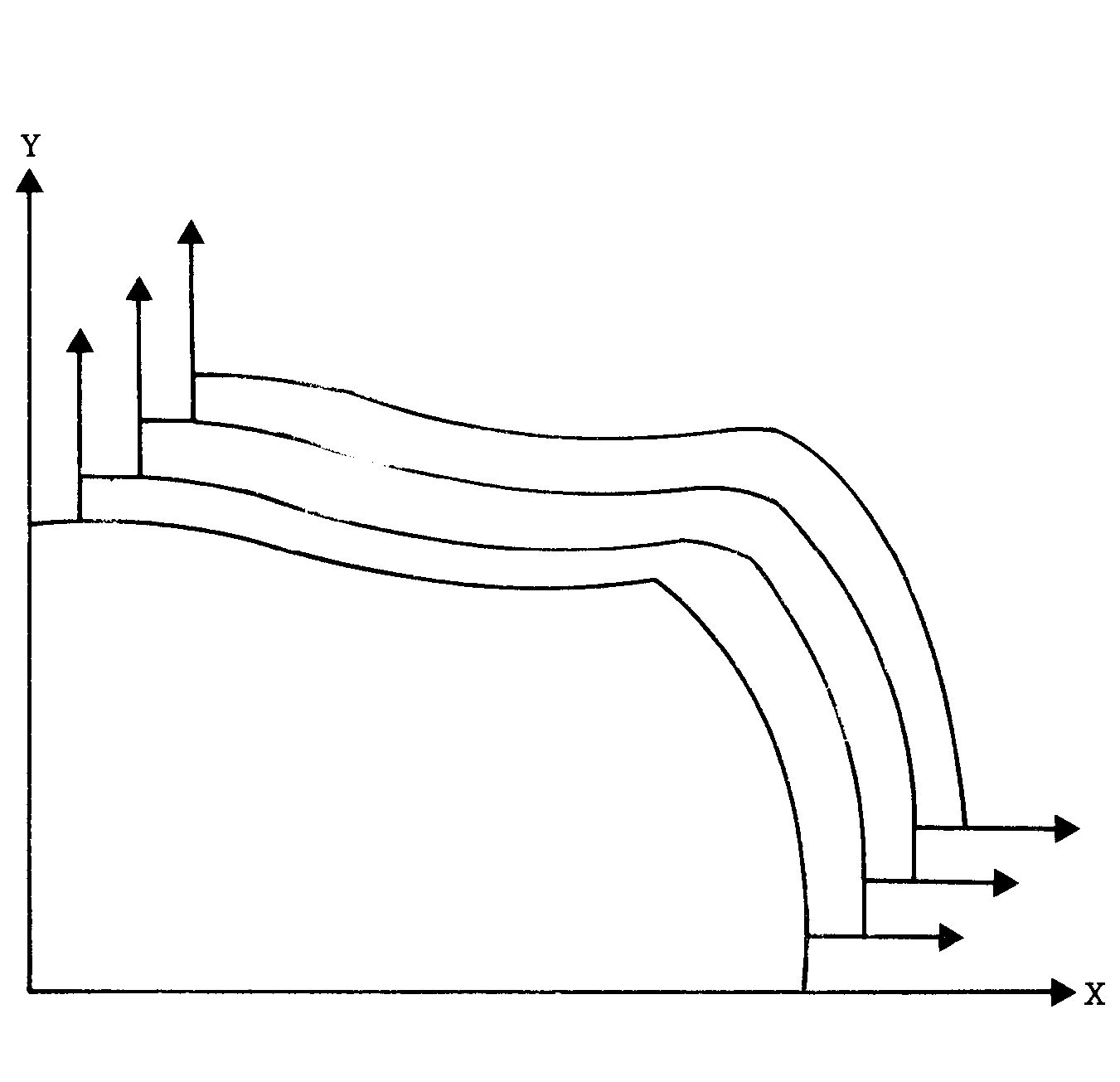
Im Bild sind sie, damit man das erkennen kann, mit Lücken gezeichnet.

Auf einer Fläche zeichenbar wird das Verfahren dann, wenn man jede X-Y-Ebene um den Betrag ihrer Raumtiefe (das entspricht der halben Z-Koordinate) entlang der Achse Z nach rechts oben verschiebt wie in Bild 9.

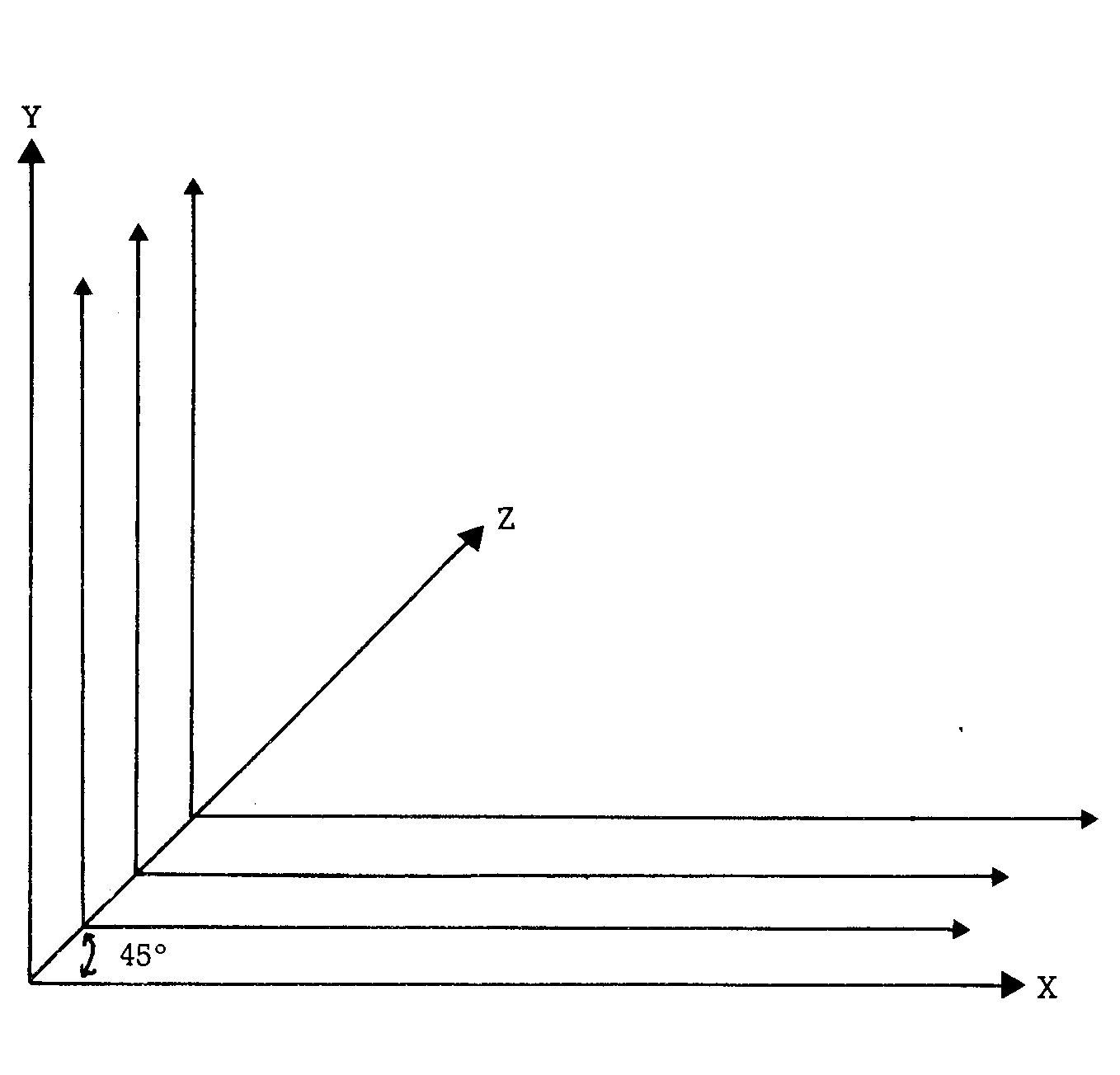
Nehmen wir nun noch an, daß auf jeder Ebene eine Kurve gezeichnet sei, die sich von Ebene zu Ebene etwas verändert, dann bekommen wir auf diese Weise aus allen Kurven zusammen den Eindruck einer räumlichen Fläche wie in Bild 10.

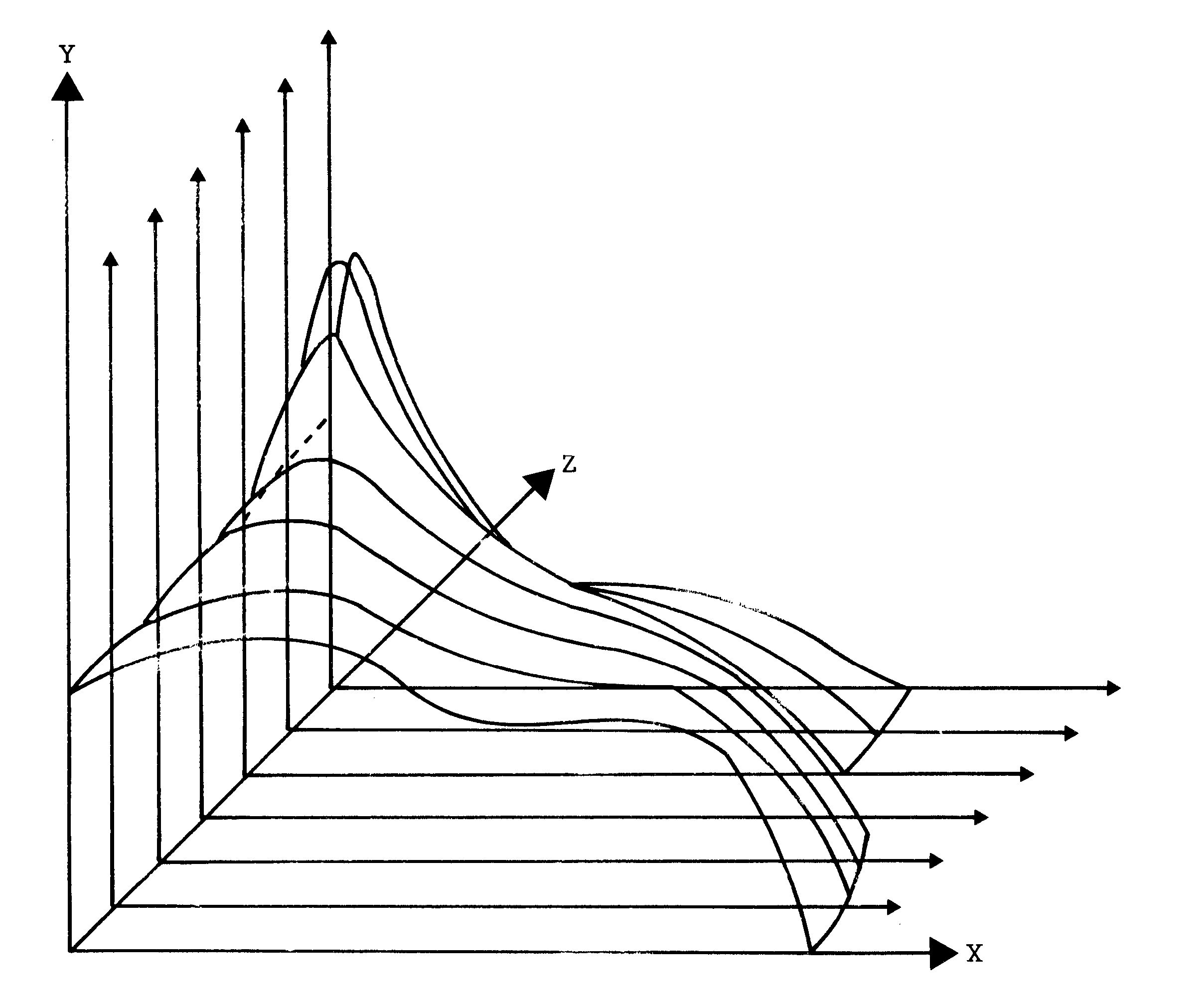
Das Prinzip ist jetzt wohl klar. Wenn wir nun bedenken, daß die Raumfläche aus lauter ebenen Kurven und die Kurven aus lauter Punkten zusammengesetzt sind, dann stellt sich für uns die Frage, wie man einen Punkt P(X1',Y1',Z1') an der richtigen Stelle unseres Bildschirmes darstellen kann. Weil wir schon wissen (von den 2D-Zeichnungen her), wie wir unser gewünschtes Koordinatensystem auf den Bildschirm bringen können, stellt sich die Frage für uns einfacher. Wir müssen uns nur noch überlegen, wie man mit zwei Koordinaten X1,Y1 den räumlichen Punkt in unserem selbstgewählten System zeichnen kann. Sehen wir uns dazu Bild 11 an.

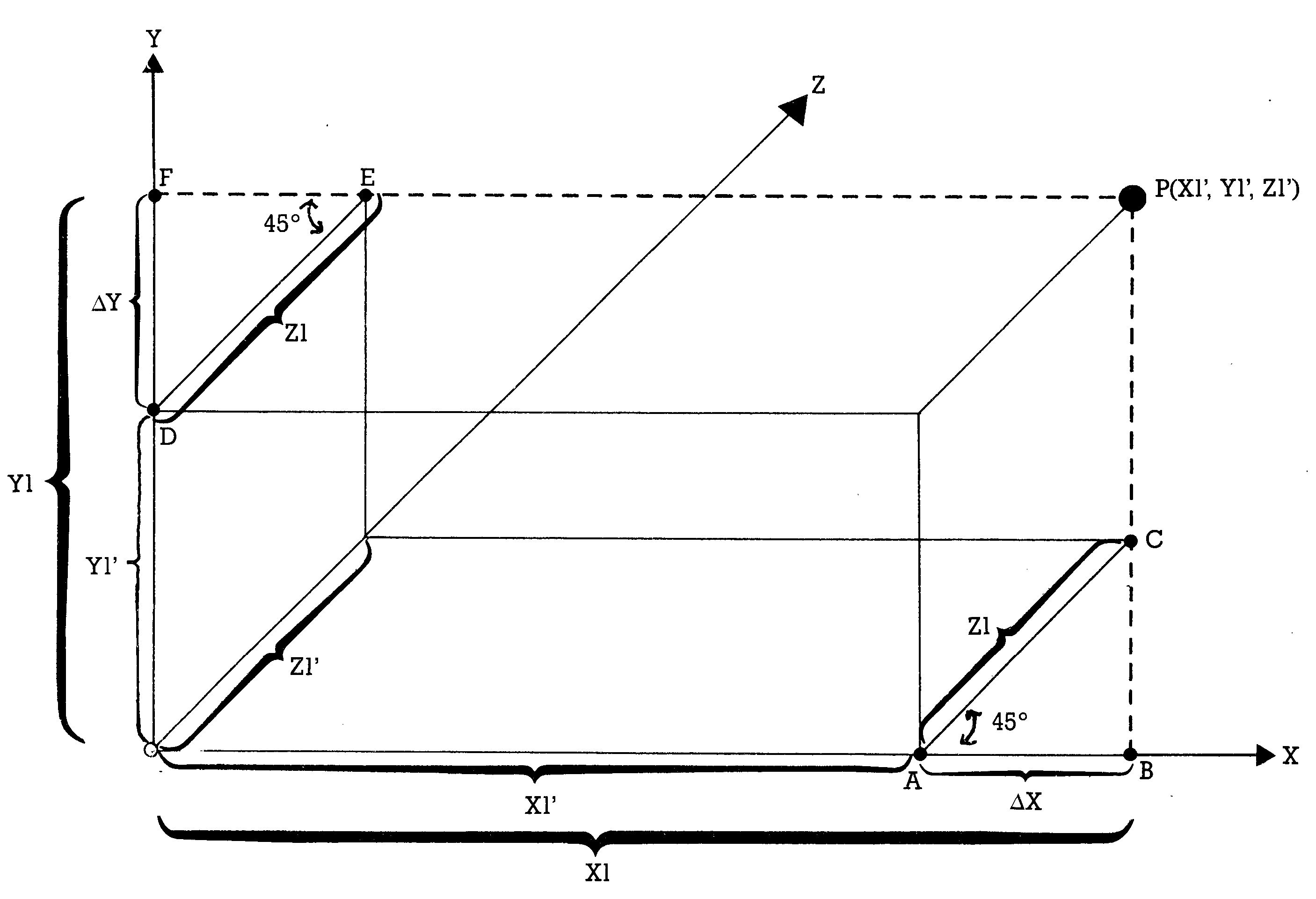
Wir haben hier einfach so getan, als gäbe es die Z-Achse gar nicht, sondern der Punkt P wäre einfach um einen Wert ΔX nach rechts und einen weiteren Wert ΔY nach oben geschoben worden. Die Koordinaten von P im ebenen System sind dann
X1 = X1' + ΔX
Y1 = Y1' + ΔY
wie man auch aus der Zeichnung sehen kann. Wie lang AX ist, kann man aus dem Dreieck ABC berechnen. Mathematisch Versierte werden mir zustimmen, daß
COS(α) = ΔX/Z1
ist und im Dreieck DEF gilt
SIN(α) = ΔY/Z1
Daraus ergibt sich dann:
ΔX = Z1*COS(α)
ΔY = Z1*SIN(α)

Weil außerdem noch nach unserer anfänglichen Vereinbarung a = 45° beträgt und die Z-Achse auf die Hälfte verkürzt ist und weil schließlich
SIN(45°) = COS(45°) = 1/√2 ist, ergibt sich:
ΔX = Z1'/(2*SQR(2))
ΔY = Z1'/(2*SQR(2))

Beide sind also gleich und für unser eigenes Koordinatensystem hat der Punkt P die Koordinaten:
X1 = X1' + Z1'/(2*SQR(2))
Y1 = Y1' + Z1'/(2*SQR(2))

Damit ist unser Problem gelöst. Denn X1', Y1' und Z1' sind die vorgegebenen Koordinaten und X1,Y1 können jetzt mit unseren Transformationen X = FNX(X1),Y=FNY(Y1) in Bildschirmkoordinaten umgerechnet werden. Wir verschachteln nun zwei Schleifen ineinander wie in Bild 12 und lassen uns damit Kurve für Kurve zeichnen.

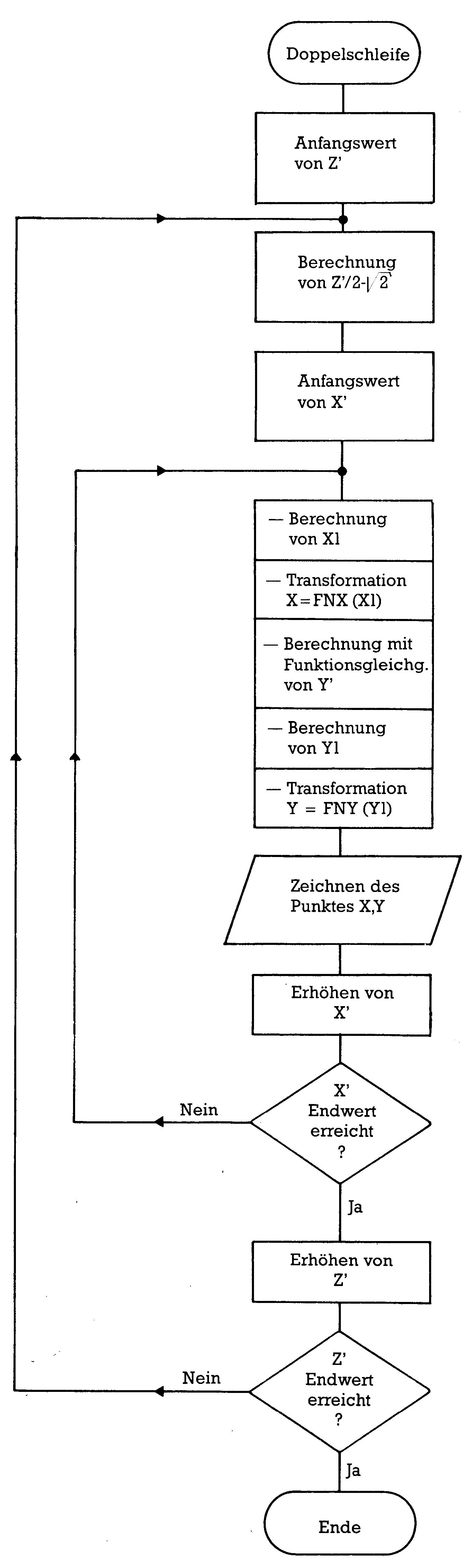
Nun wollen wir auch für die 3D-Grafik ein Programm entwerfen. Tippen Sie also NEW ein, laden Sie die Grafik-Unterprogramme und erwecken Sie unser 3D-Dornröschen mit dem nachfolgenden Aufrufprogramm.

5 POKE 52,92:POKE 56,92
100 DEFFNX(X) = (X-XU)/(XO-XU) *319
105 DEFFNY(Y) = (YO-Y)/(YO-YU) *199
110 DEFFNZ(Z) = Z/(2*SQR(2))
140 DEFFNA(X) = SIN(Z)*COS(X)
150 PRINTCHR$(147)CHR$(17)CHR$ (18)"UNSER SYSTEM:"CHR$(146): PRINT:PRINT
160 INPUT"XU,XO = ";XU,XO:INPUT ”YU,YO = ”;YU,YO

Jetzt wird es ein bißchen kompliziert, weil wir darauf achten müssen, daß die Z-Achse noch auf dem Bildschirm paßt. Wir lassen uns berechnen und anzeigen, wie groß ZO höchstens sein darf und wie klein ZU:
162 Z3 = 2*X0*SQR(2):Z4 = 2*YO* SQR(2):IF Z3<Z4 THEN PRINT "ZO MAXIMAL = "Z/3:GOTO 166
164 PRINT"ZO MAXIMAL = "Z4
166 Z5 = 2*XU*SQR(2):Z6 = 2*YU* SQR(2):IF Z5>Z6 THEN PRINT ”ZU MINIMAL = "Z5:GOTO170
168 PRINT" ZU MINIMAL="Z6
170 PRINT:INPUT" ZU,ZO=‘’;ZU,ZO: Z1=FNZ(ZO):Z2=FNZ(ZU)

Im nachfolgenden geht es nach dem (nicht immer angebrachten) Motto: Vertrauen ist gut, Kontrolle besser:
172 IF Z1>YO OR Z1>YO THEN 162
174 IF Z2<XU OR Z2<YU THEN 162

Dann lassen wir uns die Freiheit der Farbenwahl:
180 PRINT:INPUT"ZEICHEN- UND HINTERGRUNDFARBE = ";F1,F2

Nach dem Anschalten der Hochauflösung zeichnen wir die Achsen:
190 GOSUB 50100:X1 = FNX(XU):Y1 = FNY(0):X2 = FNX(XO):Y2 =Y1: GOSUB 50060
192 XI = FNX(O):Y1 = FNY(YU):X2 = X1:Y2 = FNY(YO):GOSUB 50060
194 X1 = FNX(Z2):Y1 = FNY(Z2):X2 = FNX(Zl):Y2 = FNY(Z1):GOSUB 50060

Wir könnten jetzt mit den beiden ineinandergeschachtelten Schleifen beginnen, wenn es da nicht noch das Problem der Schrittweite in den Schleifen gäbe. Die Schrittweite von X haben wir schon im 2D-Programm verwendet:
200 DX = (XO-XU)/319

Die Schrittweite von Z ist nicht so einfach zu fassen, weil man ja, je nach Kurvenart, mal weitere und mal engere Schritte machen muß. Deswegen halten wir diese Schrittweite veränderlich und lassen uns vorher nochmal danach fragen:
202 DZ = A*(Z1-Z2)/(FNX(Z1)-FNX (Z2))
182 INPUT"SCHRITTWEITE VON Z(CA.8) = ";A:PRINT

Mit Zeile 202 hätten wir bei A = 1 die selbe Punktauflösung wie in der X-Schleife. Das ist meistens zu eng und A sollte deshalb Werte um etwa 8 haben.

Es ist ganz gut, sich auch die Freiheit offenzulassen, von wo bis wo unsere Raumfläche zu zeichnen ist. Es sieht einfach besser aus, wenn sie nicht bis zum Rand des Bildschirms reicht. Die Schleifen sollten also nicht von ZU bis ZO und von XU bis XO reichen, sondern von den Anfangswerten ZA beziehungsweise XA bis zu den Endwerten ZE beziehungsweise XE. Auch diese Werte müssen abgefragt werden:
184 PRINTCHR$(18)"UNSERE ZEICHNUNG:"CHR$(146):PRINT
185 INPUT"X-BEREICH XA,XE = ";XA,XE
186 INPUT"Z-BEREICH ZA,ZE = ";ZA,ZE
Jetzt kommen die Schleifen:
210 FOR Z = ZA TO ZE STEP DZ:ZZ = FNZ(Z)
220 FOR XX = XA TO XE STEP DX:X1 = XX + ZZ
230 X = FNX(X1):YY=FNA(XX):Y1 = YY+ZZ:Y=FNY(Y1):GOSUB 50040
240 NEXT XX
250 NEXT Z

Abschließend muß wieder zurückgeschaltet werden auf den Normalbildschirm:
300 GET A$:IF A$ = "" THEN 300
310 GOSUB 50030
320 END

So! Nun können Sie das ganze vorsichtshalber abspeichern und dann mit RUN starten. Aber fassen Sie sich in Geduld. Bis das Bild komplett ist, vergehen zirka 21 Minuten. Probieren Sie mal die Eingaben:
XU=-1,XO = 6,YU=-2,YO = 6,ZU=-1, ZO = 6, Schrittweite von Z = 8, XA = 0, XE = 4,ZA = 0,ZE = 4.

Es wird Ihnen sicherlich aufgefallen sein, daß ich zu Beginn des Programms den gleichen Zeilennummernabstand wie beim 2D-Programm verwendet habe. Sie können, genauso wie dort, nun noch unseren Trick zur Funktionseingabe einsetzen. Wenn Sie das getan haben, ist unser 3D-Programm komplett und Sie können nach Herzenslust Funktionen ausprobieren. Allerdings kommt es zum Erreichen einer besonders schön aussehenden Raumfläche nur dann, wenn Sie die ganzen Eingaben zu Beginn des Programms wohlüberlegt machen oder aber mehrere Male ausprobieren.

Diese Menge an Eingaben hat zwar den Vorteil, daß man sehr frei in der Gestaltung des Ergebnisses ist, aber eine gewisse Automatik wäre schon ganz angenehm. Das überlasse ich Ihnen, denn der Programmaufwand dazu würde den Rahmen dieser Folge sprengen.

Auf ein anderes Problem werden wir in der nächsten Folge eingehen: Wie verhindert man, daß auch Linien gezeichnet werden, die eigentlich beim realen Körper (oder bei der Fläche) nicht sichtbar sind, weil sie hinter anderen Teilen der Zeichnung verschwinden?

Ich hoffe, daß diese Folge nicht allzu schwierig war. Sollten Sie Probleme mit dem mathematischen Teil haben, trösten Sie sich, indem Sie die Programme einfach so abtippen. Oder stellen Sie Fragen per Leserbrief. Ich werde mich bemühen, alle zu beantworten.